📌 페널티 회귀분석(Pedalized Regression Analysis)
- 지나치게 많은 독립변수를 갖는 모델에 페널티를 부과하는 방식으로 보다 간명한 회귀모델을 생성한다.
- 모델의 성능에 크게 기여하지 못하는 변수의 영향력을 축소하거나 모델에서 제거한다.
- 최소자승법에 의한
잔차(관측값-예측값)의 제곱합과 페널티항의 합이 최소가 되는 회귀계수를 추정한다.
페널티 회귀분석(Pedalized Regression Analysis)
- 라쏘 회귀분석(Lasso Regression)
- 릿지 회귀분석(Ridge Regression)
- 엘라스틱넷 회귀분석(Elasticnet Regression)
⭐ 라쏘 회귀분석(Lasso Regression) ⭐
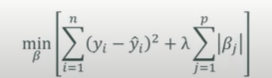
- L1 : 회귀계수의 절댓값의 합
- 모델의 설명력에 기여하지 못하는 독립변수의 회귀계수를 0으로 만든다
L1 페널티항으로 회귀모델에 페널티를 부과함으로써 회귀계수를 축소한다.- lambda : 페널티의 크기를 조절한다.
- 라쏘 회귀분석에서 페널티는 모델에 대한 기여도가 낮은 회귀계수를 0으로 만든다 (제거 된다)
- 변수 선택을 통해 설명력이 우수한 독립변수만을 모델에 포함할 수 있고, 모델의 복잡성을 축소한다.
- 전체 독립변수가 아닌 보다 작은 규모의 독립변수를 모델에 포함한다.
⭐ 릿지 회귀분석(Ridge Regression) ⭐
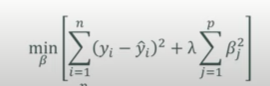
- L2 : 회귀계수의 제곱합의 합
- 모델의 설명력에 기여하지 못하는 독립변수의 회귀계수 크기를 0에 근접하도록 축소한다.
- 0에 가깝도록 축소하지만, 0이 되지는 않는다.
L2 페널티항으로 회귀모델에 페널티를 부과함으로써 회귀계수를 축소한다.- lambda : 페널티의 크기를 조절한다.
- lambda가 증가함에 따라 페널티의 영향은 커지게 되고 릿지 회귀모델의 회귀계수는 작아지게 된다.
- lambda가 매우 큰 값이라면 회귀계수는 0에 근접한다.
- 독립변수의 척도에 크게 영향을 받으므로 릿지 회귀분석 적용 전 표준화 과정이 필요하다.
- 릿지 회귀분석은 회귀모델의 모든 독립변수를 포함하므로 모델의 단순화 효과는 제공하지 못한다.
⭐ 엘라스틱넷 회귀분석(Elasticnet Regression) ⭐
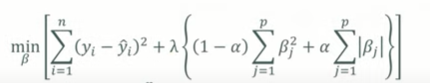
- L1과 L2를 모두 이용하여 회귀모델에 페널티를 부과한다.
- lambda : 페널티의 크기를 조절한다.
- alpha : 릿지와 라쏘의 혼합 정도를 통제한다.
alpha=0이면,릿지 회귀분석이 된다.alpha=1이면,라쏘 회귀분석이 된다.
한 번의 성능 평가만으로는 라쏘와 릿지 중 무엇이 우수하다고 말할 수 없다. 특정 데이터셋에 대한 교차검증을 바탕으로 어느 기법이 우수한지 평가한다.
- 교차검증
하나의 데이터 셋을 바탕으로 여러 개의 훈련데이터와 테스트데이터를 생성하고, 여러차례 성능 평가 후 평균을 낸다.
📌 성능평가지표
- MSE(Mean Squared Error)
- RMSE(Root Mean Squared Error) : 값이 작을수록 우수하다.
- MAE(Mean Absolute Error) : 값이 작을수록 우수하다.
- R-sqaured : 모델의 설명력을 의미하므로 값이 클수록 우수하다.
Boston 데이터 셋을 이용하여 세 가지 기법을 적용 후 성능 비교해보자.
ex) 미국 보스턴 지역의 주택가격과 주변 환경에 대한 데이터 셋
- 예측 변수 : 1~13번째 변수
- 결과 변수 : 14번째 변수
13개의 예측변수로 결과변수인 예측 가격을 예측해보자.
> str(Boston)
'data.frame': 506 obs. of 14 variables:
$ crim : num 0.00632 0.02731 0.02729 0.03237 0.06905 ...
$ zn : num 18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
$ indus : num 2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
$ chas : int 0 0 0 0 0 0 0 0 0 0 ...
$ nox : num 0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
$ rm : num 6.58 6.42 7.18 7 7.15 ...
$ age : num 65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
$ dis : num 4.09 4.97 4.97 6.06 6.06 ...
$ rad : int 1 2 2 3 3 3 5 5 5 5 ...
$ tax : num 296 242 242 222 222 222 311 311 311 311 ...
$ ptratio: num 15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
$ black : num 397 397 393 395 397 ...
$ lstat : num 4.98 9.14 4.03 2.94 5.33 ...
$ medv : num 24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...📌 훈련 데이터와 검증 데이터로 분할
createDataPartition(y=결과변수, p=훈련 데이터 비율, list=TRUE(기본값))
> library(caret)
> set.seed(123)
> train <- createDataPartition(y=Boston$medv, p=0.7, list=FALSE)
> head(train)
Resample1
[1,] 1
[2,] 4
[3,] 10
[4,] 12
[5,] 13
[6,] 16- 훈련 데이터 생성
> Boston.train <- Boston[train, ]
> nrow(Boston.train)
[1] 356- 테스트 데이터 생성
> Boston.test <- Boston[-train, ]
> nrow(Boston.test)
[1] 150📌 모델 생성
glmnet() 함수의 인수
- x : 예측변수
- 예측변수는 행렬 형식으로 지정해야 한다.
- 예측변수는 숫자 변수만 가능하므로 범주형 변수는 더미변수로의 변환이 필요하다.
- y : 결과변수
- 결과변수는 벡터 형식으로 지정해야 한다.
- family : 결과변수의 확률분포
- 연속형 : 'gaussian'
- 'binomial', 'poisson', 'multinomial', 'cox', 'mpaussian'
- alpha : 0(릿지), 1(라쏘), 0~1(엘라스틱넷)
- lambda : 페널티 크기 조정 (회귀게수 크기의 축소 정도), 교차검정을 통해 lambda값 확인한다.
x, y 사전 처리 작업이 필요하다.
> library(glmnet)- 예측변수 x 행렬 형태로 변경
model.matrix(종속변수 ~ 독립변수, 훈련 데이터 셋)
> x <- model.matrix(medv ~ ., Boston.train)
> # Intercept열 불필요하므로 삭제
> x <- model.matrix(medv ~ ., Boston.train)[, -1]
> head(x)
crim zn indus chas nox rm age dis rad tax ptratio black lstat
1 0.00632 18.0 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98
4 0.03237 0.0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94
10 0.17004 12.5 7.87 0 0.524 6.004 85.9 6.5921 5 311 15.2 386.71 17.10
12 0.11747 12.5 7.87 0 0.524 6.009 82.9 6.2267 5 311 15.2 396.90 13.27
13 0.09378 12.5 7.87 0 0.524 5.889 39.0 5.4509 5 311 15.2 390.50 15.71
16 0.62739 0.0 8.14 0 0.538 5.834 56.5 4.4986 4 307 21.0 395.62 8.47- 결과변수 y 벡터 형태로
> y <- Boston.train$medv
> head(y)
[1] 24.0 33.4 18.9 18.9 21.7 19.9⭐ 페널티 회귀분석 ⭐
📌 k-묶음 교차검증(k-fold cross-validation)
- 최적의
lambda값 찾기 위한 교차검증 - 전체 데이터 셋을
k개의 서브셋(fold)으로 분할한다. - 각 서브셋과 나머지
k-1개의 서브셋을 각각 테스트 데이터와 훈련 데이터로 사용하여 성능평가와 모델 생성 작업을 수행한다. k번의 성능 평가 결과를 평균하여 모델의 최종 성능을 산출한다.
- 릿지 회귀분석(Ridge Regression analysis) ⭐
cv.glmnet(x=예측변수 행렬, y=결과변수 벡터, family='결과변수의 확률분포(gaussian 기본값)', alpha=0)
- cv.glmnet의 family='gaussian'은 MSE를 최소로 해주는 lambda를 탐색한다.
- cv.glmnet의 type.measure='default' : 확률분포에 따라 정해진 목적함수 사용한다.
> set.seed(123)
> Boston.cv <- cv.glmnet(x=x, y=y, family='gaussian', alpha=0)
> windows(width=, height=)
> plot(Boston.cv)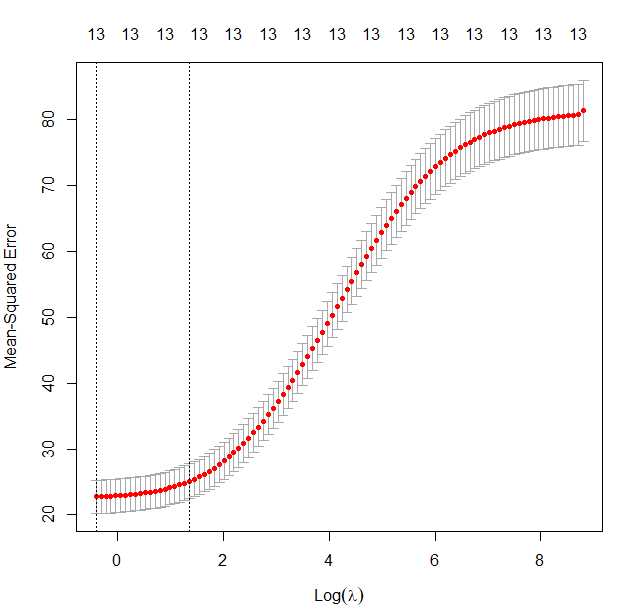
가장 왼쪽의 점선은 최적 lambda의 row값을 나타낸다. 이 값이 예측오차를 최소화 하는 log lambda 값이다. 대략 -0.4 부근으로 추정된다. 그래프 상단의 13은 예측변수의 개수이다.
> Boston.cv$lambda.min
[1] 0.6647797
> log(Boston.cv$lambda.min)
[1] -0.4082995lambda.min: num 0.665 : MSE를 최소화 하는 실제 lambda 값을 확인해본 결과 그래프로 확인한 log lambda와 일치함을 확인할 수 있다.
glmnet(x=예측변수 행렬, y=결과변수 벡터, family='결과변수의 확률분포(gaussian 기본값)', alpha=0, lambda=교차검증을 통해 찾아야 함)
postResample(pred=예측된 값, obs=실제 관측값)
# 릿지 회귀 모델
> Boston.gnet <- glmnet(x=x, y=y, family='gaussian', alpha=0, lambda=Boston.cv$lambda.min)
# 릿지 회귀 모델의 회귀계수
> coef(Boston.gnet)
14 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 26.562458173
crim -0.074637662
zn 0.017675831
indus -0.084095173
chas 3.084971492
nox -11.016754020
rm 4.080060454
age -0.003541674
dis -0.951812086
rad 0.143586748
tax -0.005498664
ptratio -0.845505137
black 0.008415669
lstat -0.432346168
# 테스트 셋의 예측변수 행렬
> Boston.test.x <- model.matrix(medv ~., Boston.test)[, -1]
# 예측
> Boston.pred <- predict(Boston.gnet, newx=Boston.test.x)
> head(Boston.pred)
s0
2 25.28493
3 30.64018
5 28.96135
6 26.05142
7 23.45445
8 20.73295
> # 예측 모델 성능 평가
> postResample(pred=Boston.pred, obs=Boston.test$medv)
RMSE Rsquared MAE
5.270168 0.707766 3.343058- 라쏘 회귀분석(Lasso Regression Analysis) ⭐
1) 예측 오차를 최소화 하는 lambda 산출
> set.seed(123)
> Boston.cv2 <- cv.glmnet(x=x, y=y, family='gaussian', alpha=1)
> plot(Boston.cv2)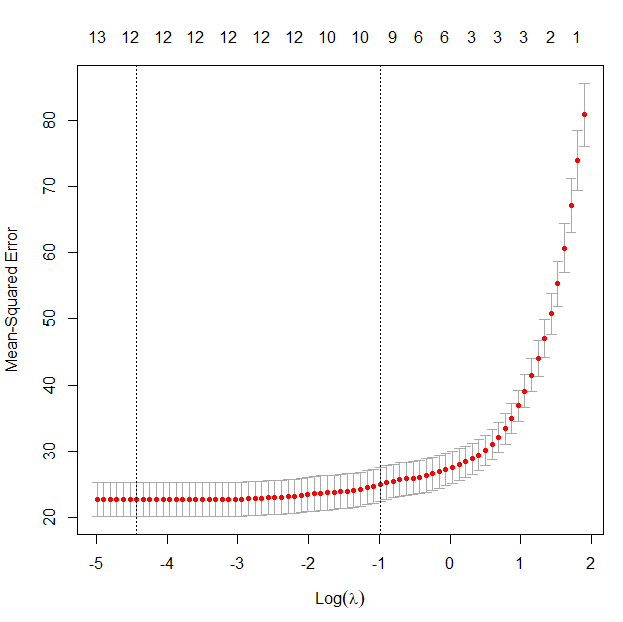
왼쪽의 점선이 예측오차를 최소화 하는 log lambda를 나타낸다.
라쏘 회귀분석은 중요하지 않은 회귀계수는 0으로 만들기 때문에 log lambda에 따라 상단의 예측변수 개수가 변화한다.
> Boston.cv2$lambda.min
[1] 0.01189058
> log(Boston.cv2$lambda.min)
[1] -4.432009
> Boston.cv2$lambda.1se
[1] 0.3716657
> log(Boston.cv2$lambda.1se)
[1] -0.9897604페널티 회귀분석은 정확도를 가능한 크게 하면서 과적합을 최소화 하는 것을 목표로 한다.
2) lambda.min vs lambda.1se를 사용할 경우의 회귀계수
> coef(Boston.cv2, Boston.cv2$lambda.min) # 1개의 예측변수가 제거됨
14 x 1 sparse Matrix of class "dgCMatrix"
s1
(Intercept) 32.720731705
crim -0.087271032
zn 0.027462832
indus -0.045858550
chas 2.904607308
nox -15.675976627
rm 3.997011835
age .
dis -1.236733449
rad 0.255230956
tax -0.009918317
ptratio -0.920530277
black 0.008606410
lstat -0.481377769
> coef(Boston.cv2, Boston.cv2$lambda.1se) # 3개의 예측변수가 제거됨
14 x 1 sparse Matrix of class "dgCMatrix"
s1
(Intercept) 16.0297569500
crim -0.0139981876
zn .
indus -0.0166198270
chas 2.0413930420
nox -2.5456625823
rm 4.3113894194
age .
dis -0.2334310319
rad .
tax -0.0007771602
ptratio -0.7681696792
black 0.0061710231
lstat -0.4700816156lambda.min 보다 lambda.1se 모델이 더 간명하다.
3) lambda.min vs lambda.1se를 사용할 경우의 성능 비교
Boston.gnet_1 <- glmnet(x=x, y=y, family='gaussian',
alpha=1, lambda=Boston.cv2$lambda.min
> Boston.pred_1 <- predict(Boston.gnet_1, newx=Boston.test.x)
> postResample(pred=Boston.pred_1, obs=Boston.test$medv)
RMSE Rsquared MAE
5.1150340 0.7197637 3.3091787> Boston.gnet_2 <- glmnet(x=x, y=y, family='gaussian',
+ alpha=1, lambda=Boston.cv2$lambda.1se)
> Boston.pred_2 <- predict(Boston.gnet_2, newx=Boston.test.x)
> postResample(pred=Boston.pred_2, obs=Boston.test$medv)
RMSE Rsquared MAE
5.5656605 0.6795993 3.6151777- RMSE와 MAE값을 비교했을 때 lambda.1se 모델이 더 크다.
- R-squared값을 비교했을 떄 lambda.mse 모델이 더 높다.
- 두 모델을 비교해봐을 때 lambda.mse 모델의 성능이 더 좋다.
- 엘라스틱넷 회귀분석(Elasticnet Regression Analysis) ⭐
1) train() 함수를 통한 인수 튜닝
caret 패키지의 train() 함수를 통해 인수 튜닝을 통해 비교적 쉽게 최적의 alpha와 lambda를 탐색할 수 있다.
train(form=결과변수 ~ 예측변수, data=훈련 데이터, method=모델 함수 이름)
trControl=trainControl(method=표본 추출 방법, number=k 개수, tuneLength=튜닝할 파라미터 개수)
method='cv' : k-fold 교차검증
> set.seed(123)
> Boston.cv3 <- train(form=medv ~ ., data=Boston.train, method='glmnet',
+ trControl=trainControl(method='cv', number=10),
+ tuneLength=10)2) 교차검증 결과로 가장 우수한 성능을 보이는 alpha와 lambda 확인
> Boston.cv3$bestTune
alpha lambda
6 0.1 0.20208123) 모델 생성
> Boston.gnet3 <- glmnet(x=x, y=y, family='gaussian',
+ alpha=Boston.cv3$bestTune$alpha,
+ lambda=Boston.cv3$bestTune$lambda)4) 회귀계수
> coef(Boston.gnet3) # 1개의 변수가 제거됨
14 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 29.766401348
crim -0.078819914
zn 0.021807176
indus -0.064680920
chas 2.966225220
nox -13.617871871
rm 4.056442437
age .
dis -1.097715391
rad 0.194940136
tax -0.007343684
ptratio -0.891291598
black 0.008443963
lstat -0.4666148495) 성능 평가
> Boston.pred3 <- predict(Boston.gnet3, newx=Boston.test.x)
> postResample(pred=Boston.pred3, obs=Boston.test$medv)
RMSE Rsquared MAE
5.1766444 0.7148912 3.3115941📌 세 가지 페널티 회귀분석 성능 비교
- 예측 정확도에 큰 차이가 없다면 더 간명한 모델을 선택하는 것이 바람직하다
- 과적합의 위험을 줄여주기 때문이다.
- lambda 생성
> lambda <- 10^seq(-5, 5, length=100)
> head(lambda)
[1] 1.000000e-05 1.261857e-05 1.592283e-05 2.009233e-05 2.535364e-05 3.199267e-05- 릿지 회귀 모델
caret 피키지의 train() 함수를 통해 100개의 lambda에 대한 교차검증 수행하고 최적의 릿지 회귀모델 생성한다.
expand.grid(alpha=0, lambda=lambda) : 그리드 생성 작업 간단히 시행 가능
1) 교차검증 및 모델 생성
> set.seed(123)
> Ridge <- train(form=medv ~ ., data=Boston.train, method='glmnet',
+ trControl=trainControl(method='cv', number=10),
+ tuneGrid=expand.grid(alpha=0, lambda=lambda))- 최종 모델 : finalModel
- 최종 모델의 lambda : 모델lambda
2) 최종 모델의 회귀계수
> coef(Ridge$finalModel, Ridge$bestTune$lambda)
14 x 1 sparse Matrix of class "dgCMatrix"
s1
(Intercept) 26.531756149
crim -0.074428914
zn 0.017800440
indus -0.084013662
chas 3.079990715
nox -10.929321371
rm 4.075749392
age -0.003350370
dis -0.950562016
rad 0.143524673
tax -0.005528583
ptratio -0.844792464
black 0.008418506
lstat -0.4333228993) 성능 평가
> Ridge.pred <- predict(Ridge, Boston.test)
> postResample(pred=Ridge.pred, obs=Boston.test$medv)
RMSE Rsquared MAE
5.2697535 0.7078302 3.3430299 - 라쏘 회귀 모델
1) 교차검증 및 모델 생성
> set.seed(123)
> Lasso <- train(form=medv ~ ., data=Boston.train, method='glmnet',
+ trControl=trainControl(method='cv', number=10),
+ tuneGrid=expand.grid(alpha=1, lambda=lambda))2) 최종 모델의 회귀계수
> coef(Lasso$finalModel, Lasso$bestTune$lambda)
14 x 1 sparse Matrix of class "dgCMatrix"
s1
(Intercept) 31.750980901
crim -0.082082764
zn 0.024769646
indus -0.048386732
chas 2.888983790
nox -15.018198838
rm 4.023977582
age .
dis -1.184753810
rad 0.230959052
tax -0.008902657
ptratio -0.912986045
black 0.008456390
lstat -0.4806943463) 성능 평가
> Lasso.pred <- predict(Lasso, Boston.test)
> postResample(pred=Lasso.pred, obs=Boston.test$medv)
RMSE Rsquared MAE
5.1328377 0.7184223 3.3111153 - 엘라스틱넷 회귀 모델
1) 모델 생성
> set.seed(123)
> Elastic <- train(form=medv ~ ., data=Boston.train, method='glmnet',
+ trControl=trainControl(method='cv', number=10),
+ tuneLength=10)2) 최종 모델의 회귀계수
> coef(Elastic$finalModel, Elastic$bestTune$lambda)
14 x 1 sparse Matrix of class "dgCMatrix"
s1
(Intercept) 29.765523097
crim -0.078486897
zn 0.021723671
indus -0.064825528
chas 2.965478459
nox -13.585240410
rm 4.054072843
age .
dis -1.097151673
rad 0.194485494
tax -0.007329651
ptratio -0.891156341
black 0.008442569
lstat -0.4671236283) 성능 평가
> Elastic.pred <- predict(Elastic, Boston.test)
> postResample(pred=Elastic.pred, obs=Boston.test$medv)
RMSE Rsquared MAE
5.1769223 0.7148754 3.3120692📌 세 가지 페널티 회귀 모델의 성능 평가 비교
models <- list(Ridge=Ridge, Lasso=Lasso, Elastic=Elastic)
> summary(resamples(models))
Call:
summary.resamples(object = resamples(models))
Models: Ridge, Lasso, Elastic
Number of resamples: 10
MAE
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
Ridge 2.314983 3.095864 3.358949 3.350092 3.553519 4.758853 0
Lasso 2.397418 3.096038 3.354588 3.385435 3.533555 4.743889 0
Elastic 2.370271 3.091582 3.351099 3.369054 3.544919 4.741635 0
RMSE
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
Ridge 3.217597 4.220445 4.527056 4.702958 5.047501 6.966902 0
Lasso 3.386027 4.226510 4.524689 4.704632 5.047745 6.942735 0
Elastic 3.323486 4.222079 4.511393 4.699214 5.056862 6.952270 0
Rsquared
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
Ridge 0.5685060 0.7102964 0.7569726 0.7432102 0.7896808 0.8415753 0
Lasso 0.5772400 0.7069019 0.7610482 0.7425921 0.7776178 0.8465731 0
Elastic 0.5743693 0.7076979 0.7608565 0.7432037 0.7831245 0.8450374 01) RMSE
> summary(resamples(models), metric='RMSE')
Call:
summary.resamples(object = resamples(models), metric = "RMSE")
Models: Ridge, Lasso, Elastic
Number of resamples: 10
RMSE
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
Ridge 3.217597 4.220445 4.527056 4.702958 5.047501 6.966902 0
Lasso 3.386027 4.226510 4.524689 4.704632 5.047745 6.942735 0
Elastic 3.323486 4.222079 4.511393 4.699214 5.056862 6.952270 0세 모델 모두 큰 차이가 없다. 비슷한 예측 성능을 갖고 있는 것으로 보인다.
2) 통계적 검정
> summary(diff(resamples(models), metric='RMSE'))
Call:
summary.diff.resamples(object = diff(resamples(models), metric = "RMSE"))
p-value adjustment: bonferroni
Upper diagonal: estimates of the difference
Lower diagonal: p-value for H0: difference = 0
RMSE
Ridge Lasso Elastic
Ridge -0.001674 0.003744
Lasso 1 0.005418
Elastic 1 1- Upper diagonal: estimates of the difference : 세 회귀 모델 간의 RMSE의 차이 (대각선 위쪽)
- Lower diagonal: p-value for H0: difference = 0 : 귀무가설이 차이가 없다는 것에 대한 유의확률 (대각선 아래쪽)
유의확률이 1이기 때문에 세 회귀 모델 간 예측 성능에 차이가 없다.
엘라스틱넷과 라쏘 회귀모델은 예측변수 개수가 1개 줄었다.
릿지 회귀모델보다 간명하다.
따라서 엘라스틱넷 또는 라쏘 회귀모델을 사용하는 것이 바람직하다.
