[ML] 로지스틱 회귀

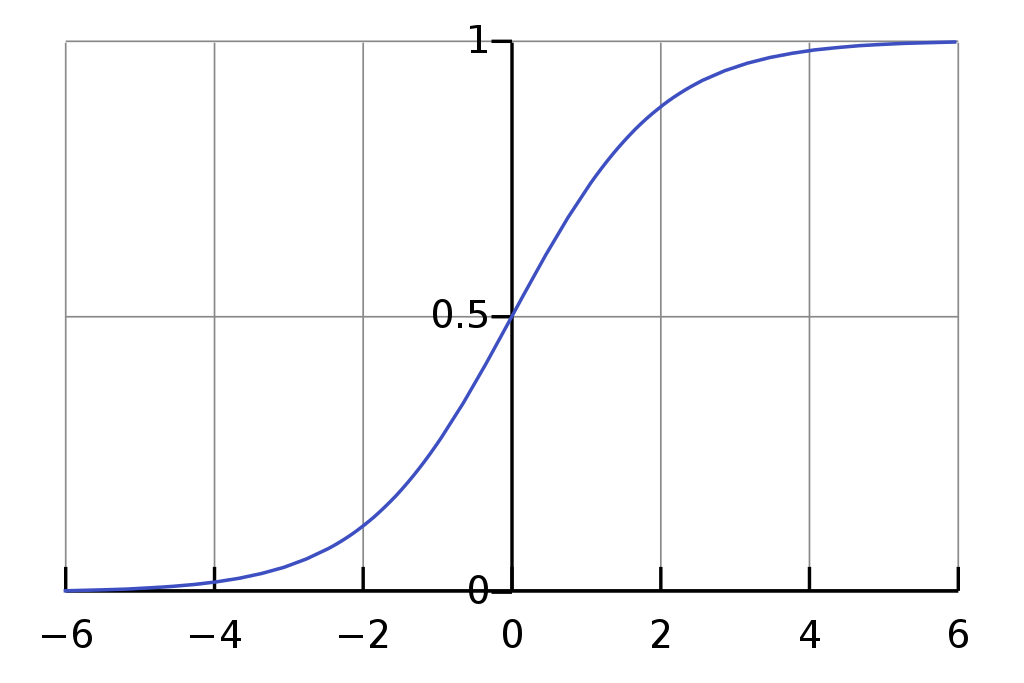
로지스틱 회귀는 선형 회귀와 마찬가지로 예측에 선형 함수를 사용한다. 하지만 회귀 모델이 아니라 분류에 사용된다. 이는 선형 회귀 모델 마지막에 시그모이드 함수를 추가해, 예측한 결과를 0과 1 사이로 압축시키는 과정으로 진행된다.

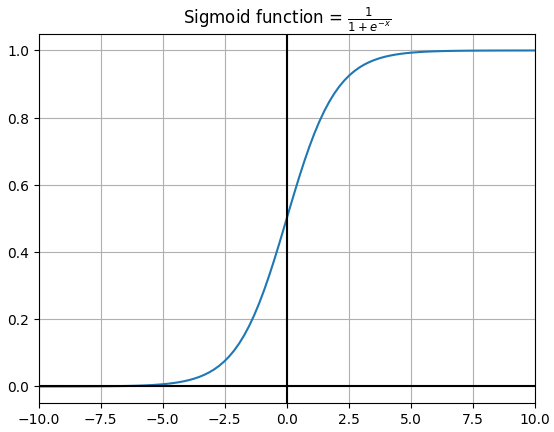
로지스틱 회귀를 구현하기 위한 코드도 선형 회귀 코드와 거의 유사하다. 예측하는 부분에서 sigmoid 함수를 적용해주는 정도의 차이이다.

class LogisticRegression:

    def __init__(self, lr=0.001, n_iters=1000):
        self.lr = lr
        self.n_iters = n_iters
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        # init parameters
        n_samples, n_features = X.shape
        self.weights = np.zeros(n_features)
        self.bias = 0

        # gradient descent
        for i in range(self.n_iters):
            y_pred = self._sigmoid(self._linear(X))

            cost = - (1 / n_samples) * np.sum(y*np.log(y_pred) + (1-y)*np.log(1-y_pred))

            dw = (1 / n_samples) * np.dot(X.T, (y_pred - y))
            db = (1 / n_samples) * sum(y_pred - y)

            self.weights -= self.lr * dw
            self.bias -= self.lr * db
            if i%100 == 99:
                print(f"{i+1}th iteration | Cost: {cost:.6g}")

    def predict(self, X):
        y_prob = self._sigmoid(self._linear(X))
        y_pred = np.where(y_prob > 0.5, 1, 0)
        return y_pred

    def _sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    def _linear(self, X):
        return np.dot(X, self.weights) + self.bias

선형 회귀 모델에서는 평균 제곱 오차를 사용했었다면 로지스틱 회귀에서는 오차를 계산하기 위한 손실 함수로 크로스 엔트로피(Cross entropy)를 사용한다.

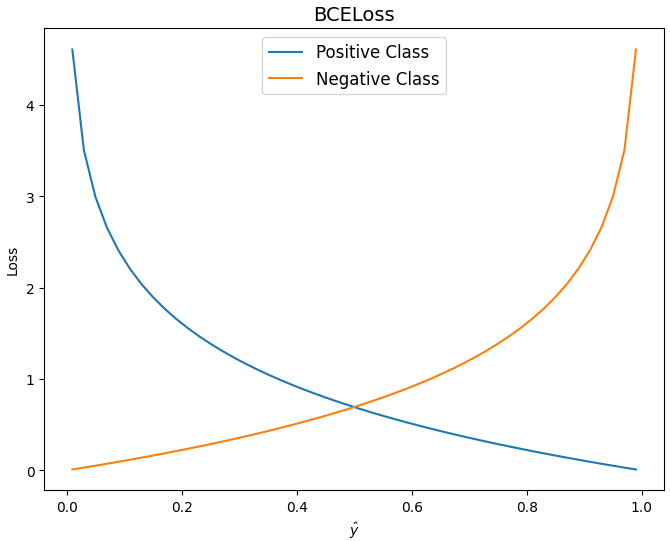
아래 그래프와 함께 보면 타겟이 1일 경우 예측값이 1에 가까울수록 손실이 줄어들고, 0에 가까울수록 손실이 급격하게 커진다. 타겟이 0일 경우에는 반대로 나타나 결국 두 클래스를 제대로 맞출 경우에 손실이 줄어들게 된다.

$y$는 클래스, $\hat{y}$는 해당 클래스일 확률이다.

더 자세한 설명

위에서 만든 로지스틱 회귀를 사용해 1차원 데이터로 예측을 해보면

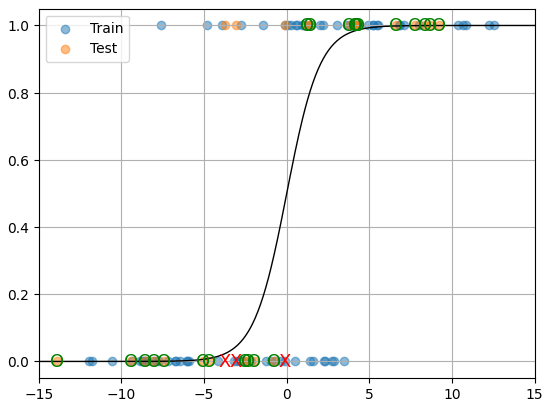
선형 회귀가 데이터를 한 평면으로 예측하는 것처럼 로지스틱 회귀는 한 평면을 기준으로 레이블을 나누게 된다. 여기서는 0.5를 기준으로 데이터가 0 또는 1로 예측된 것을 볼 수 있다.

2차원 데이터를 보면 더 확실하게 보인다.

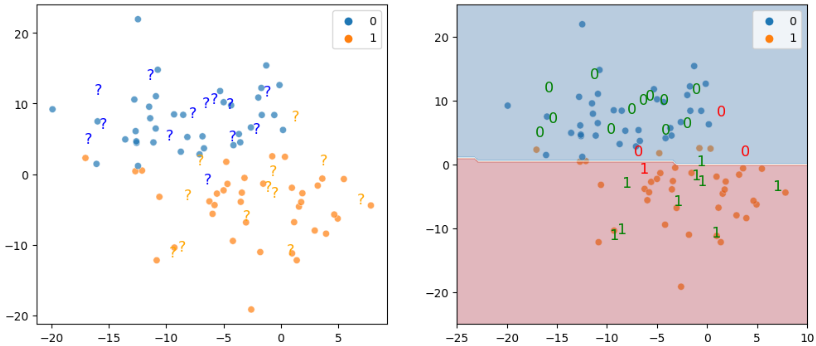
가운데 레이블을 나누는 선을 기준으로 위는 모두 0, 아래는 모두 1로 예측한 것을 볼 수 있다.

다중 레이블의 경우에는 각각의 레이블마다 하나의 레이블과 다른 모두 레이블 (OVR, one versus rest)로 나눠, 이진 분류 문제로 바꿔서 예측하게 된다.

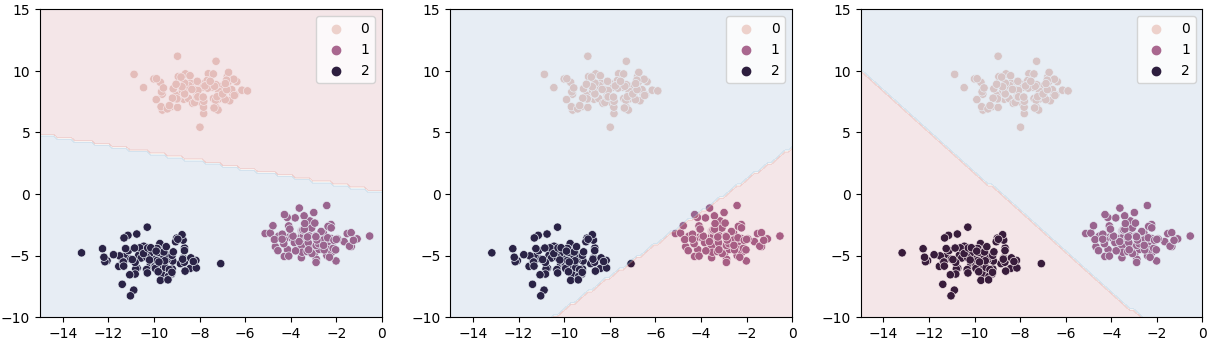
sklearn을 사용할 경우에는 아래처럼 해주면 된다. sklearn의 로지스틱 회귀를 이용할 경우에는 모델 객체를 만들 때 multi_class에 ovr 또는 multinomial을 넘겨줄 수 있는데. ovr 경우에는 위처럼 이진 분류로, multinomial은 전체 레이블로 오차를 계산한다(Cross Entropy). 기본값으로 다중레이블 분류를 진행하기 때문에 상관없다면 넘겨주지 않아도 된다. 위에 있는 BCE 손실을 여러 클래스로 확장한다면,

$y_i$는 i 번째 클래스, $\hat{y_i}$는 $y_i$ 클래스일 확률이다.

sklearn을 사용할 경우

from sklearn.linear_model import LogisticRegression

lgr = LogisticRegression()
lgr.fit(X_train, y_train)
y_preds = lgr.predict(X_test)

# 확률 반환
y_pred_probs = lgr.predict_proba(X_test)

전체 코드: github