[ML] 선형 회귀

선형 회귀 모델은 가지고 있는 데이터들의 특성들과 그에 해당하는 레이블을 선형 관계로 표현하는 모델이다. 식으로 표현을 해보면

$\hat{y} = wx + b \qquad···①$

로 값을 예측하게 된다. $\hat{y}$는 예측 값, $x$는 데이터의 특성이다. $w$(가중치)와 $b$(편향)는 모델에 훈련 데이터를 학습시키면서 업데이트 되는 값이다. 이 모델의 최종 목표는 위 식을 통해 예측한 $\hat{y}$과 실제 값 $y$의 오차를 최소화 시키는 가중치와 편향 값을 찾는 것이다.

모델의 파라미터(가중치, 편향)은 오차로부터 업데이트 된다. 아래 그림처럼 오차는 가중치, 편향, 오차, 3차원의 형태로 나타난다고 볼 수 있다. 오차가 낮을 수록 모델의 성능이 좋기 때문에 가중치와 편향은 오차가 낮아지는 방향으로 업데이트 된다.

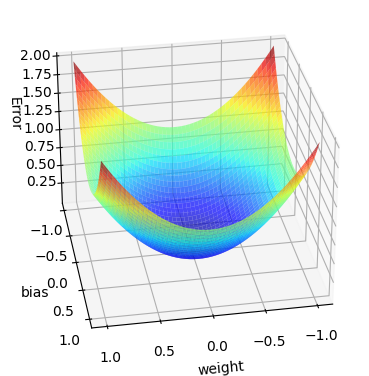
아래로 내려가도록 하는 방법은 파라미터들에 대한 오차의 변화율을 구해서 그 반대 방향으로 모델 파라미터들을 업데이트 시켜주면 된다. 한 번 업데이트 할 때 변화율의 얼마만큼을 사용할지 learning rate(lr)를 정해줘서 학습 속도를 조절해 줄 수 있다.

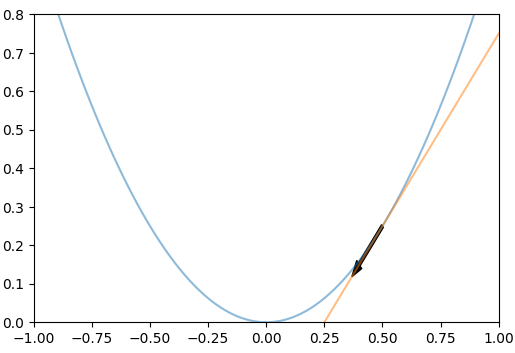
학습률을 너무 높게 잡을 경우에는 최적값에 도달하지 못하고, 너무 낮게 잡았을 경우에는 최적값에 도달하기 전에 학습이 종료될 수도 있어서 적절한 값을 선택해야한다.

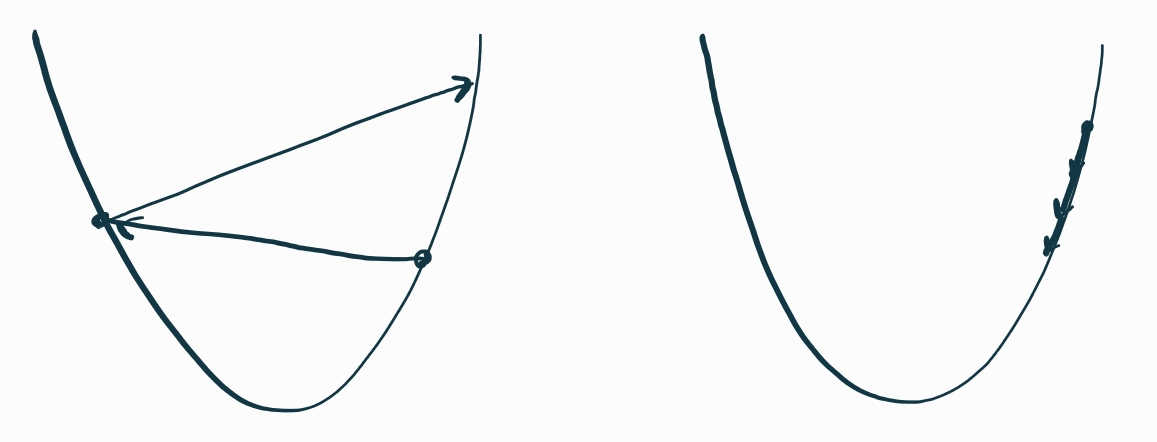← 학습률이 너무 큰 경우        학습률이 너무 작은 경우→

오차를 평균 제곱 오차(MSE)로 계산한다면
$MSE=J(w, b)=\displaystyle\frac{1}{N}\sum{(y_i - (wx_i+b))^2}\qquad\qquad\,\,···②$

$J'(w, b) = \begin{bmatrix}\frac{dJ}{dw}\\ \frac{dJ}{db}\end{bmatrix}\ =\begin{bmatrix}\frac{1}{N}\sum-2x_i(y_i-(wx_i+b))\\ \frac{1}{N}\sum-2(y_i-(wx_i+b))\end{bmatrix}\qquad···③$

코드로 구현할 때는 numpy의 dot을 써주면 된다.
위 식으로 변화량을 구한 후 파라미터들을 업데이트 해준다.

$w\leftarrow w-\mu\frac{dJ}{dw}$
$b\leftarrow b-\mu\frac{dJ}{db}$

class LinearRegression:

	# 초기값 설정
    def __init__(self, lr=0.001, n_iters=1000):
        self.lr = lr # 학습률
        self.n_iters = n_iters # 반복 횟수
        self.weights = None # 가중치
        self.bias = None # 편향

    def fit(self, X, y):
        # 학습 파라미터 초기화
        n_samples, n_features = X.shape # [데이터 수, 특성 수]
        self.weights = np.zeros(n_features) # 가중치 초기화
        self.bias = 0 # 편향 초기화

        for _ in range(self.n_iters):
            y_predicted = np.dot(X, self.weights) + self.bias # 예측, 1번 식에 해당한다.
            # 각 파라미터에 대한 오차 변화율 계산. 3번 식에 해당한다.
            dw = (1/n_samples) * np.dot(X.T, (y_predicted - y)) 
            db = (1/n_samples) * np.sum(y_predicted - y)
			
            # 파라미터 업데이트
            self.weights -= self.lr * dw
            self.bias -= self.lr * db

    def predict(self, X):
  		# fit 메서드와 같은 방법으로 예측한다.
        y_predicted = np.dot(X, self.weights) + self.bias
        return y_predicted
   
# 오차로는 평균 제곱 오차를 사용했다.
def mse(y_true, y_pred):
    return np.mean((y_true-y_pred)**2)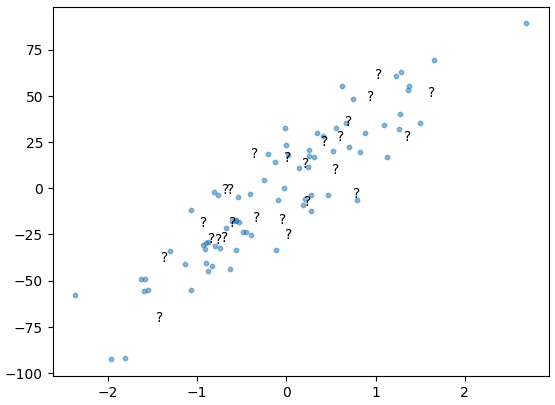

이 데이터를 사용했을 때

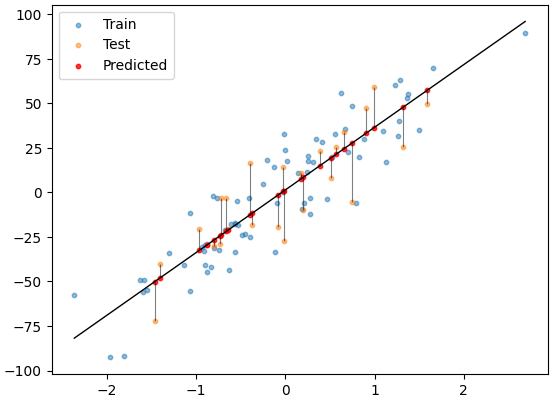
처럼 예측하게 된다.

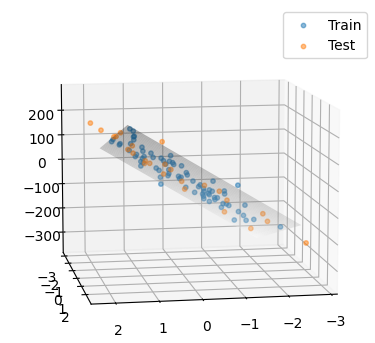
데이터의 특성이 1개가 아니라 N개의 경우에는 데이터를 가장 잘 표현하는 N차원 평면으로 예측을 하게 된다.

전체 코드: github