[책 정리] Chapter 02. 순환

2.1 순환의 소개

• 순환(recursion): 어떤 알고리즘이나 함수가 자기 자신을 호출하여 문제를 해결하는 프로그래밍 기법

순환

• 순환은 본질적으로 순환적으로 정의된 문제나 자료구조를 다루는 프로그램에 적절
  ex) 팩토리얼 함수 계산, 피보나치 수열, 이항 계수 계산, 각종 이진 트리 알고리즘, 이진 탐색, 하노이탑 문제

<프로그램 2.1.1> 순환적인 팩토리얼 계산 프로그램

int factorial(int n){
	if(n <= 1) return 1;
    else return n * factorial(n-1);
}

factorial(3) = 3 * factorial(2);
			 = 3 * 2 * factorial(1);
             = 3 * 2 * 1
             = 3 * 2
             = 6

<프로그램 2.1.2> 출력문이 추가된 순환적인 팩토리얼 계산 프로그램

int factorial(int n){
	printf("factorial (%d)\n",n);
	if(n <= 1) return 1;
    else return n * factorial(n-1);
}

순환 호출의 내부적인 구현

• 하나의 함수가 자기 자신을 다시 호출하는 것은 다른 함수를 호출하는 것과 동일
  • 복귀주소가 시스템 스택에 할당되고, 호출되는 함수를 위한 매개변수(parameter)와 지역 변수를 스택으로부터 할당 받음
    -> 함수를 위한 시스템 스택에서의 공간을 활성 레코드(activation record)라고 함
  • 호출된 함수의 코드의 시작 위치로 점프(만약, 호출된 함수가 자기 자신이라면 자기 자신의 시작 주소로 점프)
  • 호출된 함수가 끝나게 되면 시스템 스택에 복귀 주소를 호출하여 호출한 함수로 되돌아가게 됨

순환 알고리즘의 구조

• 순환 알고리즘의 구조: 자기 자신을 순환적으로 호출하는 부분 + 순환 호출을 멈추는 부분

순환 <-> 반복

• 프로그래밍 언어에서 되풀이하는 방법: 반복(iteration), 순환(recursion)

<프로그램 2.1.3> 반복적인 팩토리얼 계산 프로그램

int factorial_iter(int n){
	int k, v = 1;
    for(k = n; k > 0; k--){
    	v = v * k;
    }
    return v;
}

장점: 순환 알고리즘은 이해하기 쉽고, 쉽게 프로그램 할 수 있따.
단점: 수행 시간돠 기억 공간의 사용에 있어서 비효율적인 경우가 많음

순환의 원리

• 분할 정복(divide and conquer): 주어진 문제를 더 작은 동일한 문제들로 분해하여 해결하는 방법
  * 순환 호출이 일어날 때마다 문제의 크기가 작아짐

순환 알고리즘의 성능

• 반복 알고리즘으로 구현한 팩토리얼 -> O(n), 순환 알고리즘으로 구현한 팩토리얼 -> O(n)
• 반복 알고리즘과 순환 알고리즘이 시간 복잡도는 같지만 순환 호출의 경우 여분의 기어 공간이 더 필요하고, 또한 함수를 호출하기 위해서는 함수의 파라미터들을 스택에 저장하는 것과 같은 사전 작업이 상당히 필요함

Quiz

1. 다음과 같은 함수를 sub(10)으로 호출하는 경우에 어떤 값이 반환되는가?

int sub(int n){
	if(n < 0) return 0;
    return n + sub(n-3);
}

sub(10) = 10 + sub(7)
		= 10 + 7 + sub(4)
        = 10 + 7 + 4 + sub(1)
        = 10 + 7 + 4 + 1 + sub(-2)
        = 10 + 7 + 4 + 1 + 0
        = 10 + 7 + 4 + 1
        = 10 + 7 + 5
        = 10 + 12
        = 22
        

2. 위의 함수를 반복 기법을 이용하여 반복 함수로 다시 작성하시오.

int sub(int n)
{
    int sum = 0;
    for (int i = n; i > 0;i-=3){
        sum += i;
    }
    return sum;
}

2.2 거듭 제곱 값 계산

<프로그램 2.2.1> 반복적인 거듭제곱 계산 프로그램

int slow_power(double x, int n){
    double r = 1.0;
    for(int i=0;i<n;i++){
    	r = r*x;
    }
    return r;
} // -> O(n)

<알고리즘 2.2.1> 순환적인 거듭제곱 계산

power(x,n)

if n=0
	return 1;
else if n이 짝수
	then return power(x^2,n/2);
else if n이 홀수
	then return x * power(x^2,(n-1)/2);
    
 (1) n이 짝수인 경우
 power(x,n) = power(x^2, n/2)
 			= (x^2)^(n/2)
            = x^2^(n/2)
            = x^n
 (2) n이 홀수인 경우
 power(x,n) = x * power(x^2,(n-1)/2)
 			= x*(x^2)^((n-1)/2)
            = x * x^(n-1)
            = x^n

<프로그램 2.2.2> 순환적인 거듭제곱 계산 프로그램

double power(double x, int n){
	if(n == 0) return 1;
    else if(n%2 == 0) return power(x*x, n/2);
    else return x*power(x*x,(n-1)/2);
} // -> O(logn)

-> 반복적인 거듭제급 계산보다 순환적인 거듭제곱 계산이 더 빠름, 순환을 호출할 때마다 문제의 크기가 약 절반으로 줄어들기 때문

Quiz

1. power(2,6)과 같이 호출하였을 경우에 호출 체인을 그리시오

power(2,6) = power(4, 3) 
		   = 4 * power (16, 1) 
           = 4 * 16 * power(256 , 0)
           = 4 * 16 * 1
           = 4 * 16
           = 64

2. 거듭제곱 값을 계산하는 함수를 다음의 순환적인 정의를 이용하여 작성하면 실행시간이 줄어드는가?
   $x^n=\begin{cases} 1\;\;\;\;if\;\;n = 0\\ x*x^{(n-1)}\;\;\;\;if\;\;n > 0 \end{cases}$

double power(double x, int n){
    if(n == 0)
        return 1;
    else
        return x * power(x, n - 1);
}

실행시간은 줄어들지 않는다 -> O(n)

2.3 피보나치 수열의 계산

-> 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

<프로그램 2.3.1> 순환적인 피보나치 수열 계산 프로그램

#include <stdio.h>

int fib(int n){
	if(n == 0) return 0;
    else if(n == 1) retuern 1;
    else return fib(n-2) + fib(n-1);
}

fib(6) = fib(4) + fib(5)
	   = fib(2) + fib(3) + fib(3) + fib(4)
       = fib(0) + fib(1) + fib(1) + fib(2) + fib(1) + fib(2) + fib(2) + fib(3)
       = 0 + 1 + 1 + fib(0) + fib(1) + 1 + fib(0) + fib(1) + fib(0) + fib(1) + fib(1) + fib(2)
       = 0 + 1 + 1 + 0 + 1 + 1 + 0 + 1 + 0 + 1 + 1 + fib(0) + fib(1)
       = 0 + 1 + 1 + 0 + 1 + 1 + 0 + 1 + 0 + 1 + 1 + 0 + 1
       = 8

• 매우 이해하기 쉽지만 매우 비효율적, fib(6)으로 호출하였을 경우 fib(4)가 2번, fib(3)은 3번 계산됨. 이런 현상은 순환 호출이 깊어질수록 점점 심해짐

<프로그램 2.3.2> 반복적인 피보나치 수열 계산 프로그램

int fib_iter(int n){
	int tmp, current =1, last = 0;
    for(int i=2;i<=n;i++){
    	tmp = current;
        current += last;
        last = tmp;
    }
    return current;
}

Quiz

1. fib(7)이 호출되었을 경우에 fib(4)는 몇번이나 중복 계산되는가? 3번 중복 계산됨

fib(7) = fib(5) + fib(6)
	   = fib(3) + fib(4) + fib(4) + fib(5)
       = fib(3) + fib(4) + fib(4) + fib(3) + fib(4)

2. 반복적인 피보나치 수열 계산 함수의 시간복잡도? -> O(n)
3. 순환적인 피보나치 수열 계산 함수의 대략적인 시간복잡도를 추리할 수 있겠는가? 하나의 함수 호출이 두 개의 함수 호출로 나누어진다는 점에 착안하라 -> O($2^n$)

2.4 하노이탑 문제

하노이탑 조건

• 한 번에 하나의 원판만 이동할 수 있다.
• 맨 위에 있는 원판만 이동할 수 있다.
• 크기가 작은 원판 위에 큰 원찬이 쌓일 수 없다.
• 중간의 막대를 임시적으로 이용할 수 있으나 앞의 조건들을 지켜야 한다.

n개의 원판을 가지는 하노이탐 문제의 해답
1. A의 n-1개 원판을 B로 옮긴다.
2. A의 제일 밑에 있는 원판을 C로 옮긴다.
3. B의 n-1개 원판을 C로 옮긴다.

// 막대 from에 쌓여 있는 n개의 원찬을 막대 tmp를 사용하여 막대 to로 옮긴다.
void hanoi_tower(int n, char from, char tmp, char to){
	if(n == 1){
    	from에서 to로 원판을 옮긴다.
    }else{
    	1. from의 맨 밑에 있는 원판을 제외한 나머지 원판들을 tmp로 옮긴다.
        2. from에 있는 한 개의 원판을 to로 옮긴다.
        3. tmp의 원판들을 to로 옮긴다.
    }
}

• 1, 3은 막대 위치만 달라졌을 뿐 원래 문제의 축소된 형태라는 것을 발견할 수 있음. 1은 to를 사용하여 from에서 tmp로 n-1개의 원판을 이동하는 문제이고, 3은 from을 사용하여 tmp에서 to로 n-1개의 원판을 이동하는 문제

// 막대 from에 쌓여 있는 n개의 원찬을 막대 tmp를 사용하여 막대 to로 옮긴다.
void hanoi_tower(int n, char from, char tmp, char to){
	if(n == 1){
    	from에서 to로 원판을 옮긴다.
    }else{
    	hanoi_tower(n-1, from, to, tmp); // to를 사용하여 from에서 tmp로 n-1개 원판을 이동
        from에 있는 한 개의 원판을 to로 옮긴다.
        hanoi_tower(n-1, tmp, from, to); // from을 사용하여 tmp에서 to로 n-1개 원판을 이동
    }
}

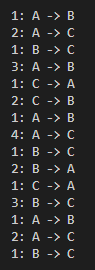
<프로그램 2.4.1> 하노이탑 문제 프로그램

#include <stdio.h>
void hanoi_tower(int n, char from, char tmp, char to){
	if(n == 1){
    	printf("원판 1을 %c에서 %c으로 옮긴다.\n",from, to);
    }else{
    	hanoi_tower(n-1, from, to, tmp);
        printf("원판 1을 %c에서 %c으로 옮긴다.\n",from, to);
		hanoi_tower(n-1, tmp, from, to);
    }
}

main(){
	hanoi_tower(4,'A','B','C');
}

반복적인 형태로 바꾸기 어려운 순환

다음 팩토리얼 예제에서 차이점

1. return n * factorial(n-1);
2. return factorial(n-1) * n;

• 꼬리 순환(tail recursion)은 1처럼 순환 호출이 순환 함수의 맨 끝에서 이루어지는 형태의 순환, 이 경우 알고리즘은 쉽게 반복적인 현태로 변환이 가능
• 머리 순환(head recursion)인 2나 하노이탑 문제처럼 여러 군데에서 자기자신을 호출하는 경우(multi recursion)는 쉽게 반복적인 코드로 바꿀 수 없음

Quiz

1. 순환을 사용하는 방법에 대한 설명 중 잘못된 것은? -> 3
   (1) 순환적으로 정의된 문제에 적합하다.
   (2) 반복을 이용하는 것보다 효율적이다.
   (3) 간접적으로 시스템 스택이 사용된다.
   (4) 순환이 될 때마다 문제의 크기는 작아진다.

2.5 다중 순환

다중 순환이란

• 순환 함수들은 호출이 발생할 때마다 몇 개의 순환 호출이 이루어지는가에 따라 선형 순환, 이진 순환 그리고 다중 순환으로 나눌 수 있음

1. 선형 순환(linear recursion): 함수의 호출이 발생하면 최대로 하나의 순환 호출이 이루어지는 경우를 말함(팩토리얼, 거듭제곱)
2. 이진 순환(binary recursion): 함수에서 두 개의 순환 호출이 발생하는 경우(피보나치 수열, 하오니 탑)
3. 다중 순환(multiple recursion): 하나의 함수에서 두 개 이상의 순환 호출이 이루어지는 경우

영역 채색 문제

영역 채색(blob coloring), 연결 화소 분석법(connected component labeling): g흑과 백의 화소 값만을 갖는 이진 영상(binary image)에서 연결된 객체를 찾는 방법

• 이진 영상을 스캔하다가 흰 화소를 만나면 어떤 색으로 칠함.
• 그리고 이 화소와 인접한 네 방향의 이웃 화소에 대해 순환적으로 검사하면서 같은 색을 칠함 -> 즉, 4 방향으로 순환 호출을 하는 다중 호출 사례

<프로그램 2.5.1> 영역 채색 문제 프로그램

#include <cstdio>
#define WIDTH 20
#define HEIGHT 9

using namespace std;

// 순환 호출 함수 (다중 순환의 예)
void labelComponent(unsigned char img[HEIGHT][WIDTH], int x, int y, int label)
{
    if (x < 0 || y < 0 || x >= WIDTH || y >= HEIGHT) // 영상의 밖이면 return
        return;
    if (img[y][x] == 9) { // 처리 안된 전경 화소이면
        img[y][x] = label; // label로 화소 값을 바꾸고
        labelComponent(img, x - 1, y, label); // 순환 호출: 좌측 이웃화소
        labelComponent(img, x, y - 1, label); // 순환 호출: 상측 이웃화소
        labelComponent(img, x + 1, y, label); // 순환 호출: 우측 이웃화소
        labelComponent(img, x, y + 1, label); // 순환 호출: 하측 이웃화소
    }
}

// 이진 영상의 영역 채색(blob coloring) 함수
void blobColoring(unsigned char img[HEIGHT][WIDTH])
{
    int label = 1; // label은 1부터 시작함
    for (int y = 0; y < HEIGHT; y++) { // 영상의 모든 화소에 대해
        for (int x = 0; x < WIDTH; x++) {
            if (img[y][x] == 9) // 처리가 안된 전경 화소이면
                labelComponent(img, x, y, label++); // 연결화소 채색 시작
        }
    }
}

// 영상의 화소 값을 화면에 출력하는 함수
void printImage(unsigned char img[HEIGHT][WIDTH], char* msg)
{
    printf("%s\n", msg);
    for (int y = 0; y < HEIGHT; y++) {
        for (int x = 0; x < WIDTH; x++) {
            if (img[y][x] == 0) {
                printf(".");
            } else {
                printf("%-1d", img[y][x]);
            }
        }
        printf("\n");
    }
    printf("\n");
}

// 주 함수
int main()
{
    // 입력 영상 : 자료 !
    unsigned char img[HEIGHT][WIDTH] = {
        0, 0, 0, 0, 0, 0, 9, 0, 0, 0, 0, 9, 9, 9, 9, 9, 0, 0, 9, 9,
        9, 9, 9, 9, 9, 0, 9, 0, 0, 0, 0, 0, 0, 0, 0, 9, 0, 0, 9, 9,
        0, 0, 9, 0, 0, 0, 9, 0, 0, 0, 0, 9, 9, 9, 9, 9, 0, 0, 9, 9,
        0, 9, 9, 9, 0, 0, 9, 9, 9, 0, 0, 9, 0, 0, 0, 0, 0, 0, 9, 9,
        0, 9, 0, 9, 0, 0, 9, 0, 0, 0, 0, 9, 9, 9, 9, 9, 0, 0, 9, 9,
        9, 9, 0, 9, 9, 0, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 9, 9,
        9, 0, 0, 0, 9, 0, 9, 0, 0, 0, 0, 0, 9, 0, 9, 0, 0, 0, 0, 0,
        9, 0, 0, 0, 9, 0, 9, 0, 0, 0, 0, 0, 9, 0, 9, 0, 0, 0, 9, 9,
        0, 0, 0, 0, 0, 0, 9, 0, 0, 0, 0, 9, 9, 9, 9, 9, 0, 0, 9, 9
    };

    printImage(img, (char*)"<Original image>");
    blobColoring(img);
    printImage(img, (char*)"<Labelled image>");
    return 0;
}

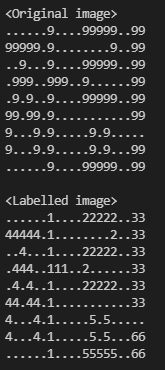
-> 입력 영상의 "자료!"란 글자의 각 연결된 부분들 (ㅈ, ㅏ, ㄹ, ㅛ, 느낌표(!)의 두 영역)이 각각의 객체가 되어 채색되었으며 전체 6개의 객체가 검출된 것을 알 수 있음.
-> 이 프로그램은 실제로 객체 영역의 크기가 크지 않은 경우 매우 안정적으로 실행됨
-> 영상의 크기가 크고, 객체 영역의 면적이 매우 넓은 경우 실행속도가 느려지며 심한 경우 스택 오버플로우가 발생할 수 있음.
-> 따라서, 일반적으로는 주사선 알고리즘(scanline algorithm)을 사용함, 반복문을 사용해서 코드가 매우 복잡하지만 처리시간이 빠르고, 영상의 크기와 상관없이 일정한 시간 안에 결과를 얻을 수 있음.

미로 탐색 문제

• 미로 찾기 문제도 순환을 이용하여 구현할 수 있음
• 어떤 위치에서 이웃하는 4 방향에 대해 순환 호출이 이루어지는 지 유의, 현재 위치가 출구의 위치와 동일하면 탐색 성공이며, 탐색이 성공하면 더 이상 순환 호출을 하지 않도록 done 변수를 true로 설정

<프로그램 2.5.2> 순환을 이용한 미로 탐색 프로그램

[Location2D.h]

struct Location2D{
    int row; // 현재 위치의 행 번호
    int col; // 현재 위치의 열 번호

    Location2D(int r = 0, int c = 0) {
        row = r;
        col = c;
    }
    
    void set(int r,int c){
        row = r;
        col = c;
    }

    // 위치 p가 자신의 이웃인지 검사하는 함수
    bool isNeighbor(Location2D &p){
        return ((row == p.row && (col == p.col - 1 || col == p.col + 1)) || (col == p.col && (row == p.row - 1 || row == p.row + 1)));
    }

    // 위치 p가 자심과 같은 위치인지를 검사하는 함수(연산자 오버로딩 사용)
    bool operator==(Location2D& p) { return row == p.row && col == p.col; }
};

#include "Location2D.h"
#include <cstdio> 
const int MAZE_SIZE = 6;

char map[MAZE_SIZE][MAZE_SIZE] = {
    { '1', '1', '1', '1', '1', '1' },
    { '0', '0', '1', '0', '0', '1' },
    { '1', '0', '0', '0', '1', '1' },
    { '1', '0', '1', '0', '1', '1' },
    { '1', '0', '1', '0', '0', 'x' },
    { '1', '1', '1', '1', '1', '1' }
};

bool isValidLoc(int r, int c){
    if(r<0 || c <0||r>=MAZE_SIZE||c>=MAZE_SIZE)
        return false;
    else
        return map[r][c] == '0' || map[r][c] == 'x';
}

Location2D locEntry, locExit; // 입구와 출구 위치
bool done = false; // 탐색 성공 여부

// 순환으로 구현한 미로 탐색 구현
void searchRecur(Location2D pt){
    printf("(%d,%d) ", pt.row, pt.col); // 현재 위치 화면에 출력
    if(done)    // 이미 탐색에 성공했다면 return
        return;
    if(pt == locExit){ // 현재 위치가 출구이면 성공
        done = true;
        return;
    }

    int r = pt.row;
    int c = pt.col;
    map[r][c] = '5';

    // 4방향 이웃에 대해 순환 호출
    if(isValidLoc(r-1,c))
        searchRecur(Location2D(r - 1, c));
    if(isValidLoc(r,c-1))
        searchRecur(Location2D(r, c - 1));
    if(isValidLoc(r+1,c))
        searchRecur(Location2D(r + 1, c));
    if(isValidLoc(r,c+1))
        searchRecur(Location2D(r, c + 1));
}

// 미로 탐색 프로그램 주 함수
int main(){
    locEntry.set(1, 0);
    locExit.set(4, 5);
    searchRecur(locEntry); // 미로 탐색 시작
    if(done)
        printf("\n ==> Find Exit.\n");
    else
        printf("\n ==> Not Find Exit.\n");

    return 0;
}

<참고자료>
천인국 · 공용해 · 하상호 지음,『C언어로 쉽게 풀어쓴 자료구조』, 생능출판(2016)
천인국 · 최영규 지음,『C++로 쉽게 풀어쓴 자료구조』, 생능출판(2016)