🧩 High Dimensional Data
📌 Eigenvalue, Eigenvector
Eigenvalue와 Eigenvector를 사람에 투영하여 설명한다면
- Eigenvalue = 외형(살이 찌거나 빠지거나, 피부가 그을리는 등)
- Eigenvector = 그사람 그 자체(다이어트를 한다고 해서 사람 자체가 바뀌지는 않음)
그래서 PCA는 Eigenvector를 축으로 하며,
Eigenvalue가 가장 커지는 쪽을 정하여 실행한다. (데이터의 특성을 가장 잘 반영하므로)
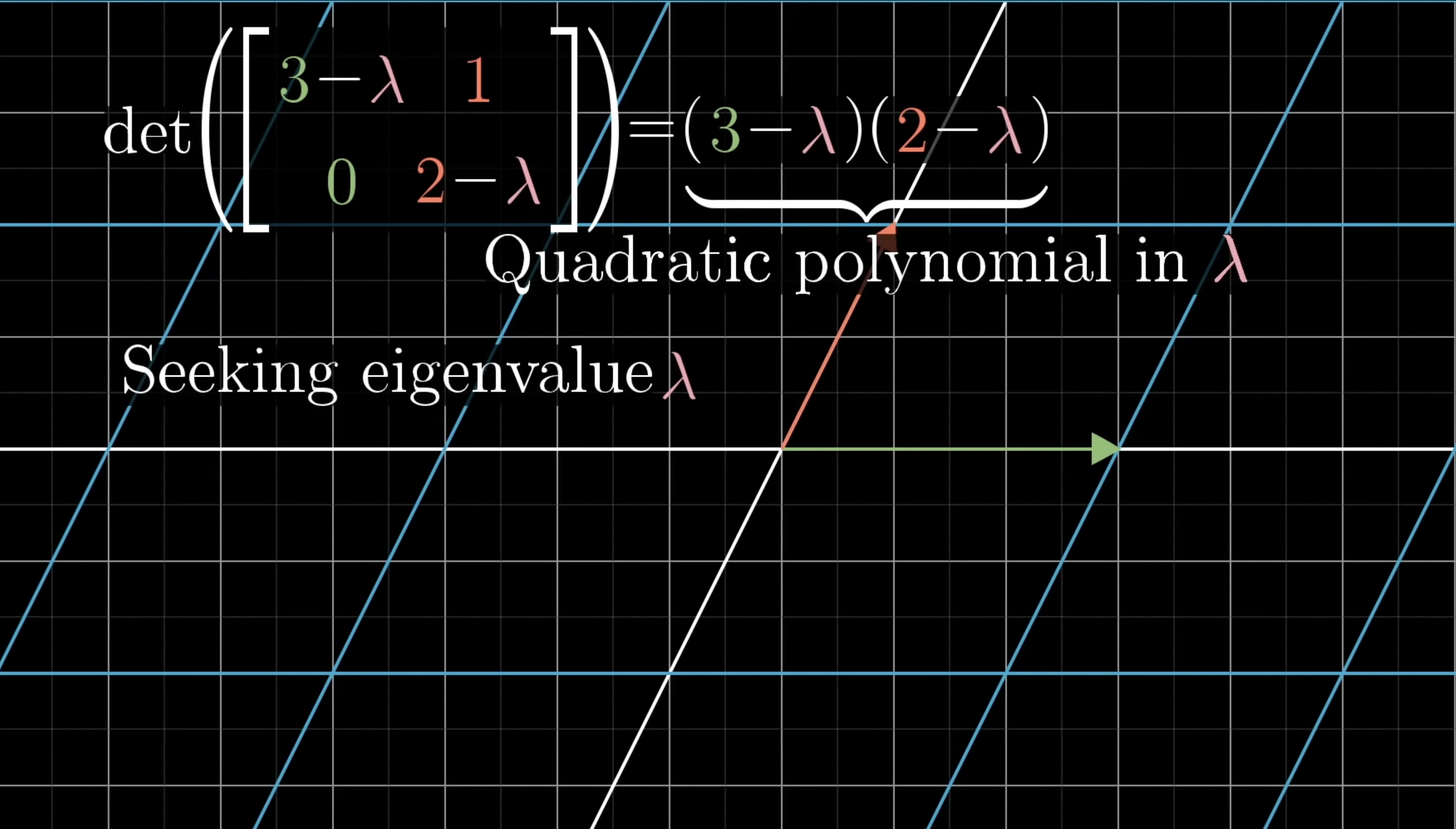
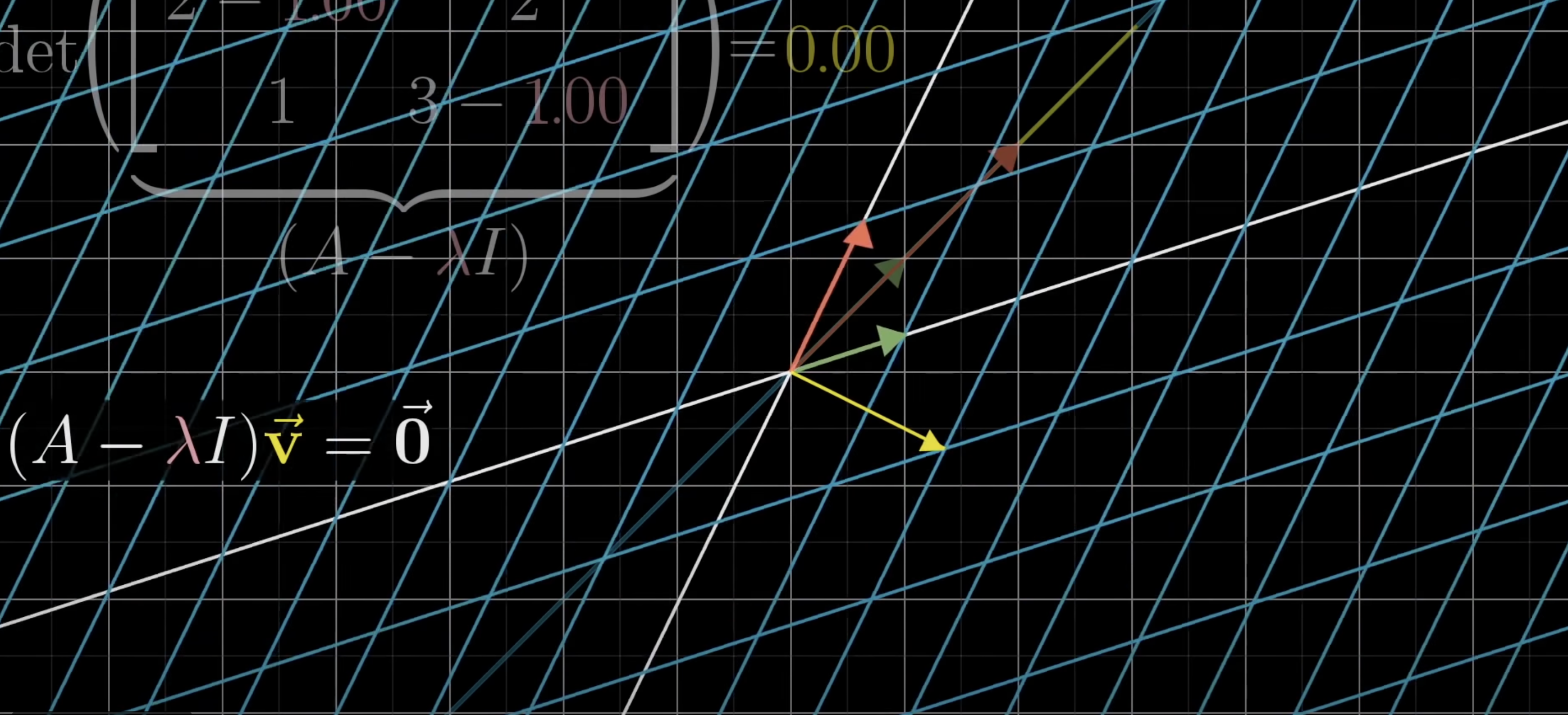Eigenvector를 축으로 해서 돌아가는 그리드를 생각해보면 된다. 그리드가 우리 입장에서는 선으로 보일 수도, 면으로 보일 수도 있다.
🏁 내 코드
import numpy as np
v = np.array([[4,2],[2,4]])
value = np.linalg.eigvals(v)
vector = np.linalg.eig(v)
print('eigenvalue=',value)
print('eigenvector=',vector)✔️np.linalg.eigvals()
numpy를 이용해 eigenvalue 구함
✔️ np.linalg.eig()
numpy를 이용해 eigenvector 구함
📌 PCA(Principal Component Analysis)
예를 들어, 고차원의 데이터 feature[a,b,c,d] 를 처리하고 비교한다고 생각해보면
[a,b], [a,c], [a,d], [b,c], [b,d], [c,d] ...
이처럼 feature가 많으면 많을 수록 분석하기가 힘들고, Overfitting이 일어난다.
Overfitting: 데이터를 분석하여 pattern만 뽑아내고 싶은데, noise까지 함께 저장되는 현상
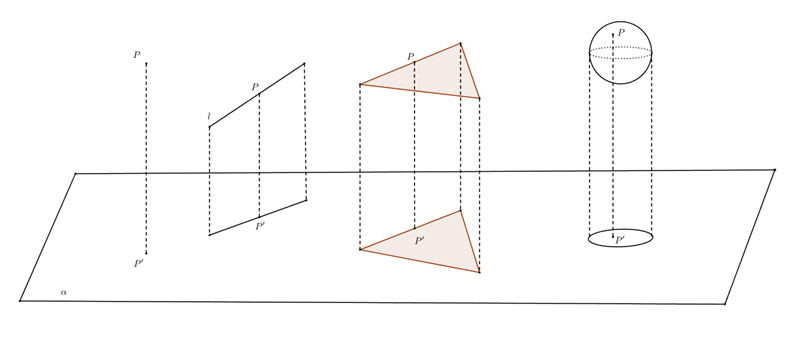
이런 현상을 피하기 위해 고차원의 데이터를 정사영하여 주성분으로 차원을 축소하는 방법.
차원을 축소하기 위해서 Eigenvalue, Eingevector 가 필요하다.
🏁 내 코드
import pandas as pd
from sklearn.preprocessing import StandardScaler, Normalizer
from sklearn.decomposition import PCA
print('Data= \n',features)
scaler = StandardScaler() # 다른 데이터들을 비교 가능하게 만들어줌
features = pd.DataFrame(scaler.fit_transform(features),columns=['bill_length_mm','bill_depth_mm','flipper_length_mm','body_mass_g']) # 노말라이즈된 데이터 얻음
print('\n Standardized features=', features)
pca = PCA(n_components=2) # 2차원으로 축소 PCA 실행
pc_df = pd.DataFrame(pca.fit_transform(features), columns=['PC1','PC2']) # PCA 시행하여 변환된 주성분으로 데이터 프레임 생성
ratio = pca.explained_variance_ratio_ # variance ratio
✔️ scaler = StandardScaler()
scale을 맞춰줘야 하는 이유?
✔️ pca = PCA(n_components=None)
pca: 주성분을 뽑아내는 것
n_components: 주성분을 몇 개로 할 것인지 정하기
Engineer