필터링의 다음 이야기는 바로 Image Pryamid 입니다.

Image Downsampling

이제 이미지를 픽셀 값들의 행렬로 생각할 수 있는 우리, 이런 생각을 해봅시다. 주어진 이미지의 크기를 작게 만드는 건 어떻게 할 수 있을까요? 가장 간단히 할 수 있는 방법은 짝수 열과 짝수 행을 없애서 붙이는 겁니다. 아래를 보시죠.

이렇게 Naive 한 방법으로 우리는 어느 정도 형태를 유지하면서 이미지의 크기를 반으로 줄여나갈 수 있습니다. 그러나, 컴퓨터에서의 이미지는 불연속적인 픽셀 값이 촘촘하게 배치된 덕분에 마치 실제처럼 연속적인 것처럼 보이는 것입니다. 그래서 결국 픽셀 값을 지운다면 (이것을 일명 pixelated, 한국어로는 '깍두기 효과'라고 부릅니다.) 굉장히 부자연스러워짐을 확인할 수 있습니다. 모양이 점점 이상해질 수 밖에 없는 거지요...

Aliasing

우리가 사는 이 세상은 연속적이라고 할 수 있습니다. (물론 분자, 원자 단위까지 쪼개면 불연속이라 할 수도 있겠지만은...) 이미 아는 내용이겠지만, 다시 한 번 우리가 이러한 세상을 이미지로 캡처하는 과정을 살펴봅시다. 먼저 빛이 어떠한 실생활의 오브젝트를 맞고 우리 카메라로 들어오게 되면 그 카메라는 이것을 픽셀에 매칭해서 값을 정해줍니다. 그렇다면 우리는 다음과 같은 결론에 도달할 수 있을 겁니다.

이미지는 연속적인 세상을 불연속적인 값으로 샘플링한 것이다.

그렇기 때문에, 우리가 해상도가 높으면 높을수록 더 조밀하게 샘플링을 하기 때문에 우리가 소위 선명하다고 느낄 수 있는 것이죠.

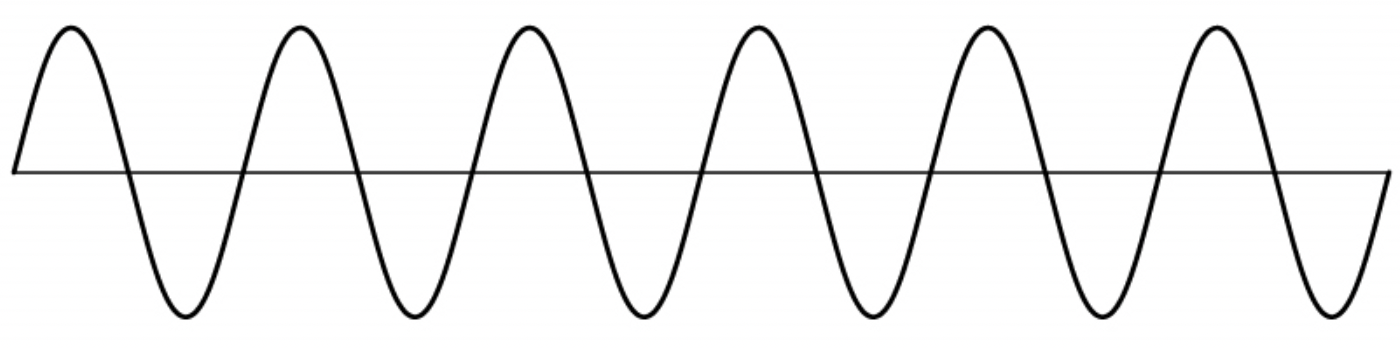
위와 같이, 실제에서 색상을 나타내는 다음과 같은 사인파가 있다고 생각해봅시다. 쉽게 말해 가장 높은 값이 하얀색, 가장 낮은 값이 검정색인거죠. 이렇게 연속적인 파동을 픽셀에 따라 샘플링을 한 예시는 아래와 같습니다.

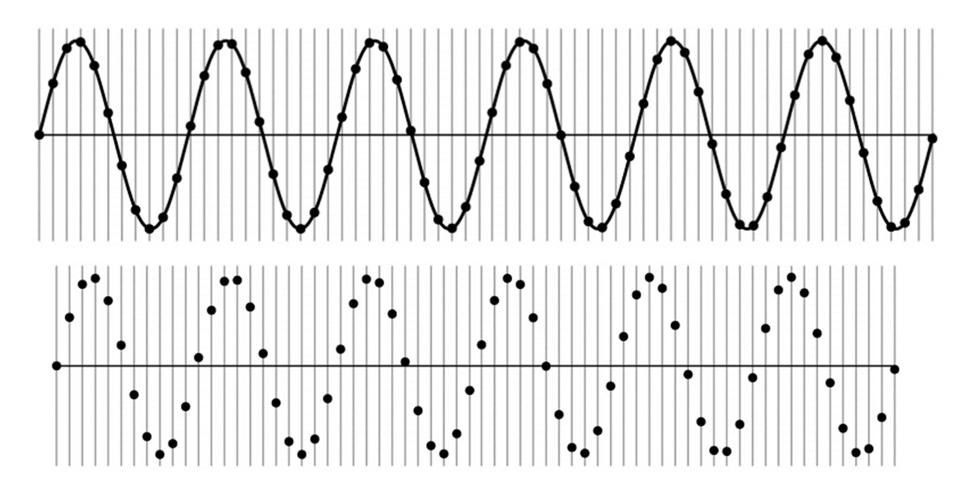
픽셀값이 오밀조밀하게 샘플링이 되어있어 discrete 한 결과도 어느정도 기존의 연속적인 사인파의 형태를 유지하는 것을 확인할 수 있습니다. 그 다음 아래 예시를 보죠.

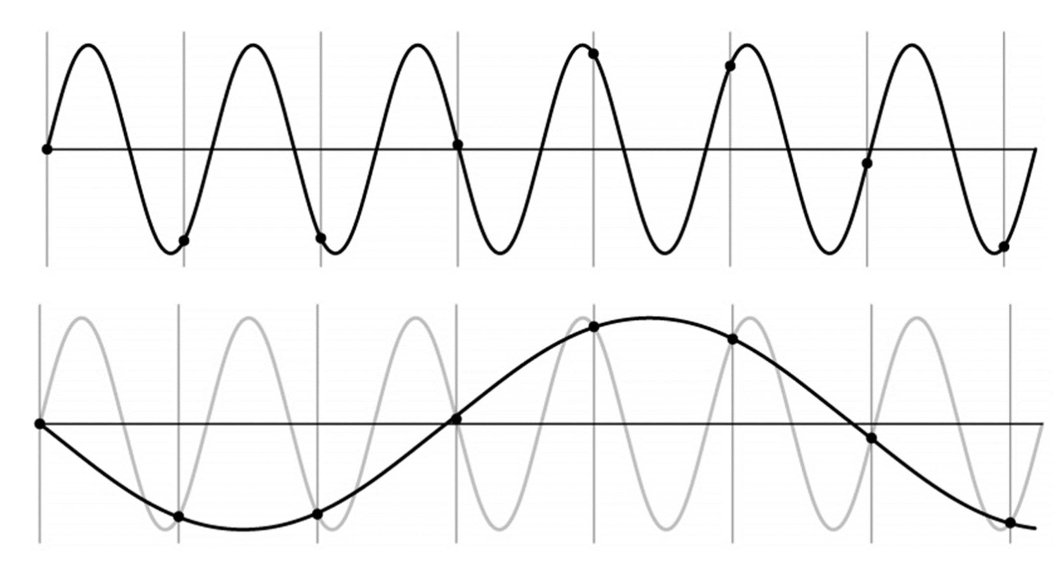
한 픽셀에 해당하는 실제 영역이 더 커져 버리면, 즉 샘플링 하는 픽셀의 구간이 넓어져 버린다면 다음과 같이 샘플링을 하고 난 뒤의 신호가 기존의 신호와 구별이 불가능해집니다. 이러한 효과를 Aliasing 이라 하는 것입니다.

위의 이미지도 위쪽 부분을 보면 Sampling Rate 의 미스 매치로 인해 똑바라야 할 격자 무늬가 다소 삐뚤삐뚤 어지러운 것을 확인할 수 있습니다.

실제로 카메라는 한 픽셀의 값을 매길 때 <R, G, B>를 포함하여 각각의 색상 성분에만 반응하는 네 개의 색상 채널에 매칭을 합니다. 그렇기 때문에 이런 Aliasing이 일어나면 특정 색에 크게 반응할 수 있습니다.

왼쪽 그림 남자의 옷은 실제로 회색이라는 하나의 색상으로 이루어져 있지만, 가슴 라인 부분을 자세히 보면 녹색이 짙은 부분을 확인할 수 있습니다. 픽셀에 해당하는 영역이 커서 마찬가지로 Sampling Rate 의 미스 매치로 인해 색에도 편향적인 영향을 미칠 수 있는 것이죠. 이러한 효과를 Moire 라고 표현하기도 합니다.

지금까지의 Aliasing은 Space (공간)의 관점에서 바라보았지만, 이것을 Temporal (시간)의 관점에서 바라볼 수도 있습니다. 우리가 보는 동영상은 실제로는 프레임 단위로 이미지를 계속 연속으로 보여주는 것에 불과합니다. 30 프레임이라는 것은 1초에 이미지를 30 번 찍는다는 것을 의미합니다. 하지만 실제에선 시간 또한 연속적인 개념이지요.

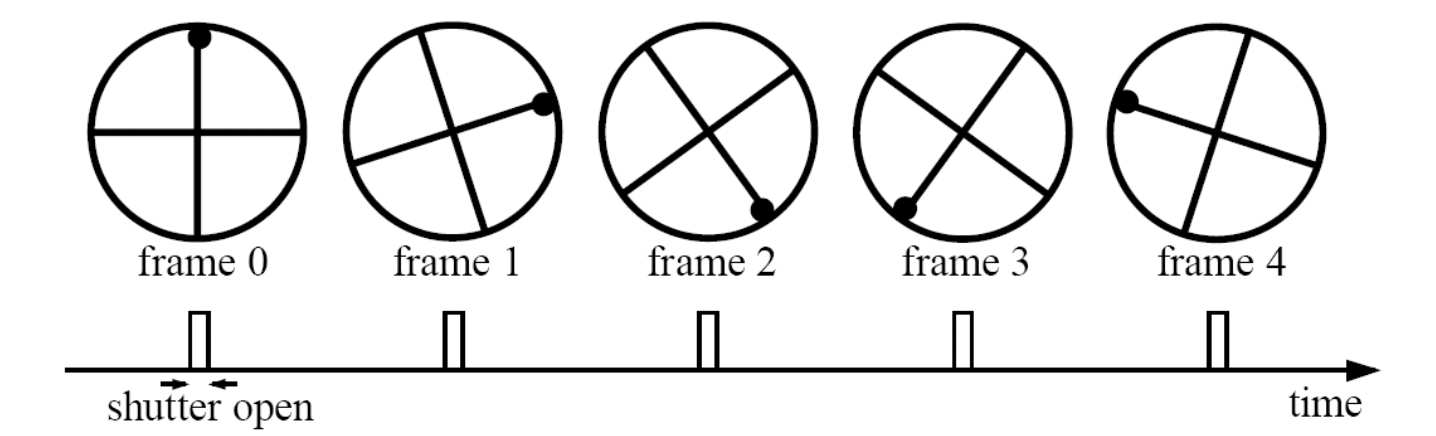
위와 같이, 오른쪽으로 돌아가고 있는 바퀴를 동영상 촬영하고 있습니다. 자 근데 여기서, 우리 저 바퀴에서 기준이 되어주는 점이 없다고 생각을 한 번 해봅시다. 그렇다면 위의 그림은 오른쪽으로 돌아가는 것처럼 보일 수도 있지만, 왼쪽으로 천천히 돌아가는 것처럼 보일 수도 있지 않을까요? 만약 프레임이 더 낮아서 90도를 돌았을 때, 한 프레임을 찍는다면 마치 돌지 않고 가만히 있는 것처럼 보일 수도 있는 겁니다. 이것은 우리가 시간축으로 샘플링을 하기 때문에 발생할 수 있는 것으로 이를 Temporal Aliasing 이라 부릅니다.

Anti-Aliasing

그렇다면 우리는 어떻게 이 Aliasing 을 없앨 수 있을까요? 첫 번째 방법은 Oversampling 입니다. 딱 한 번이 아니라 샘플링을 여러 번 해서 그 평균값을 최종적인 픽셀 값으로 하는 방법입니다.

아까 봤던 격자 무늬 예시에 Oversampling 을 적용한 모습입니다. 기존에는 흰색과 검정색만이 존재했지만 적용한 이미지의 위쪽을 보면 격자의 테두리가 평균값을 취해 회색빛이 들어있는 것을 확인할 수 있습니다.

두 번째 방법은 Smoothing 입니다. 말 그대로 Gaussian 같은 필터를 적용해서 이미지를 조금 더 부드럽게 하는 것으로, Oversampling과 느낌은 비슷합니다. 그러나, 이 방식은 어쩔 수 없이 정보 손실 을 가져오게 됩니다. 주변의 값들을 평균 내니깐요. 그래도 Aliasing 보다는 보기에 나아서 이와 같은 방법을 사용하곤 합니다.

아까봤던 Downsampling 에 Smoothing 을 적용하는 것은 얘기가 다릅니다. 짝수 열과 행을 지우기 전에 Smoothing을 해준다는 것은, 아예 없애기 전 이 값들을 반영해주는 것이 됩니다. 따라서 아래를 보면 위에서 Naive 하게 한 것보다 훨씬 결과가 깔끔한 것을 확인할 수 있습니다.

Gaussian Image Pyramid

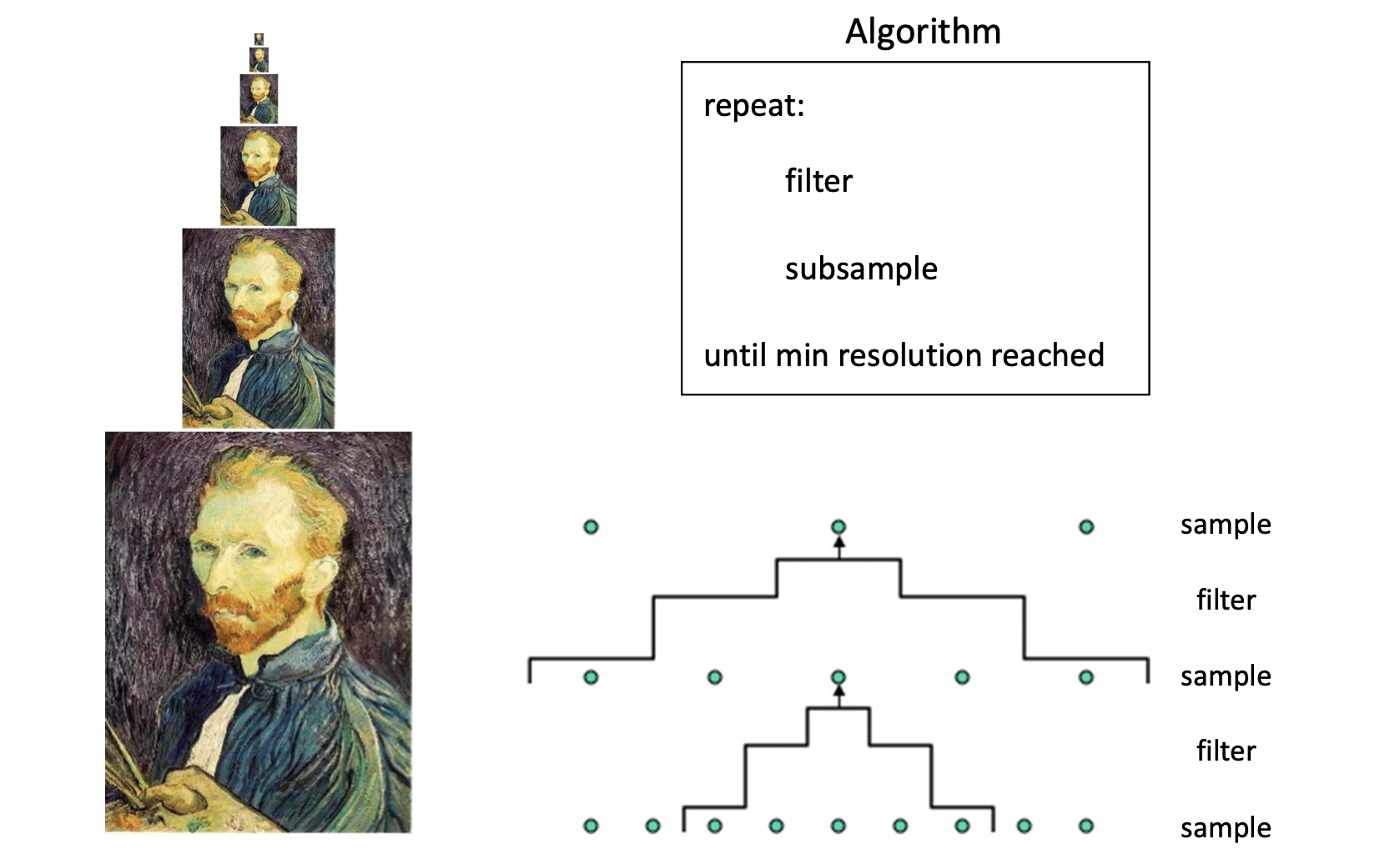
방금 설명드렸던, 두 번째 방법 을 반복적으로 수행해서 이미지의 크기를 계속해서 줄여나가 마치 피라미드 같은 모양을 하는 것을 Gaussian Image Pyramid 라고 합니다. 다시 요약하자면 Gaussian 필터를 적용해서 기존 픽셀 값을 최대 가중치로 하여 주변의 값들까지 받아들인 뒤에, 몇몇 행과 열을 제거해서 픽셀 수를 줄이는 Subsampling 을 반복하는 것을 의미합니다.

이렇게 이미지 크기를 줄여나가는 과정이 왜 필요할까요? 한 가지 예로 우리가 자주하는 게임을 들어봅시다. 이 게임은 2차원이 아닌 3차원에서 플레이 한다고 해봅시다. 그렇다면 카메라의 시점에서 거리에 따라 오브젝트의 크기가 제각기 다를 것입니다. 이를 위해, 그 오브젝트를 위와 같이 미리 Pyramid 로 해 놓는다면 거리 변화에 그때 그때 Downsampling 할 필요 없이 바로 바로 사용할 수 있게 되는 겁니다. 게임에서 생명과도 같은 Real-Time 에 훨씬 효과적일 수 있는 것이죠. ($\frac{2}{5}$ 크기의 이미지를 만들기 위해서는 $\frac{1}{2}$과 $\frac{1}{4}$ 이미지를 Interpolation 하면 될 것입니다.)

그러면 이런 의문이 될 수 있겠네요. 이렇게 미리 미리 이미지를 다 만들어 놓는다면 메모리 상으로 큰 부담이 되지 않을까요?

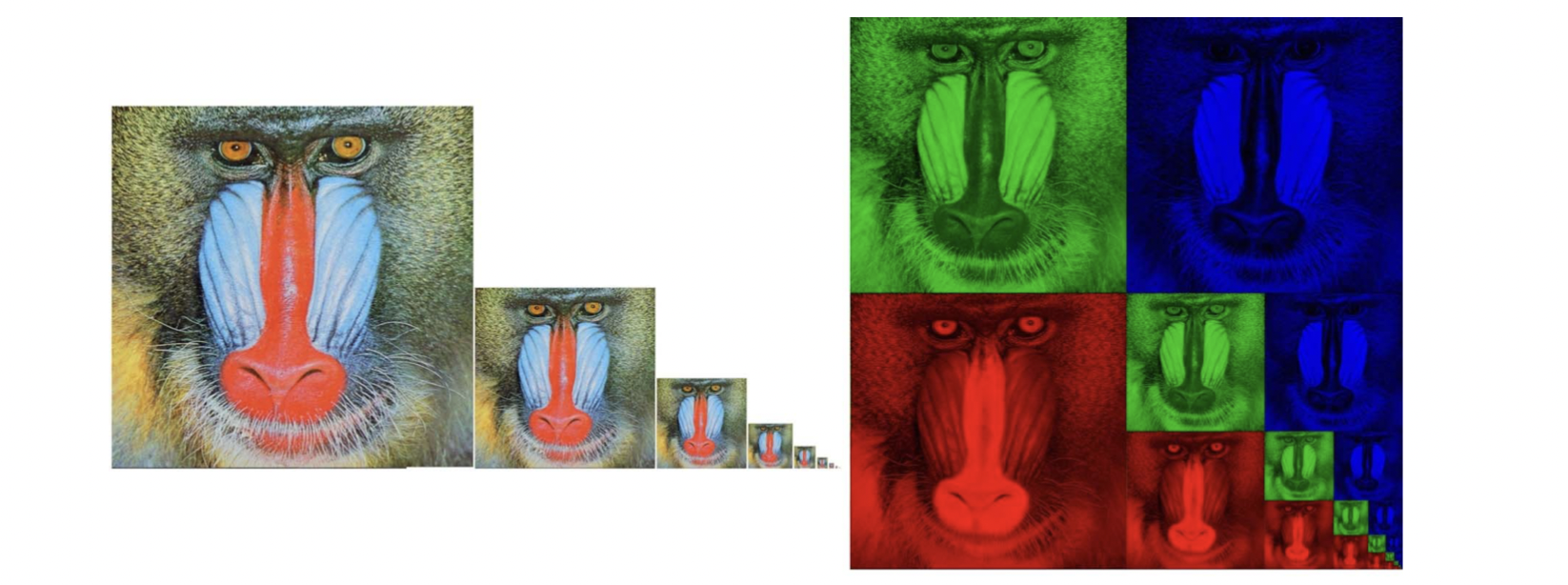
그런데 우리 생각해봅시다. $\frac{1}{2}$ 크기의 이미지를 위해 메모리는 원본 크기의 $\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}$ 만큼이 필요하게 됩니다. 마찬가지로 $\frac{1}{4}$ 크기라면 $\frac{1}{4}\times\frac{1}{4}=\frac{1}{16}$ 이 되겠지요. 그러면 이론적으로 무한번 이 과정을 수행하여야 아래의 수식처럼 고작 원본 이미지의 33%만이 추가적으로 사용되게 됩니다.

$\sum_{i=0}^{\infty}(\frac{1}{4})^i = \frac{1}{1-\frac{1}{4}} = \frac{4}{3}$

하지만 문제가 새로이 발생합니다.

우리가 결국 Gaussian으로 Smoothing 처리를 하는 것이기 때문에 정보 손실, 즉 이미지의 디테일이 많이 사라지게 되는 것이지요. 특히 위 그림의 줄무늬처럼 색이 균일하지 않는 부분의 경우에는 매우 심하지요. 더군더나, 이미 Downsampling을 수행한 이미지는 반대 방향으로 완벽하게 Reconstruction 하는 것이 불가능해지게 됩니다.

그렇습니다. Downsampling 이 있으면 Upsampling 도 생각해볼 수 있는 문제입니다. 반대로 64 $\times$ 64 이미지를 512 $\times$ 512 이미지로 만드는 것이죠. 그렇다면 이것은 한 픽셀을 가지고 8개의 픽셀을 만들어야 한다는 뜻이 됩니다. 1차원의 데이터를 8차원의 데이터로 복원한다? 이는 Computer Vision에 있어 아주 유명한 문제이며 전문 용어로는 Upsampling이 아닌 Super Resolution 이라고 합니다.

Resolution(해상도)를 올리겠다. 저해상도 이미지를 고해상도로 올리겠다는 겁니다. 이미 정보의 손실이 일어났기 때문에 사실 다시 한 번 말하지만 완벽한 Reconstruction 은 이론적으로는 불가능합니다. 하지만 이미지에는 Context 가 존재합니다. 작은 이미지라도 예를 들어 그것이 눈이라는 것을 알면 얼추 맞춰서 끼워넣을 수도 있다는 것입니다. 따라서, 요즘은 Deep Learning 을 활용해 최대한 원본에 가깝게 Super Resolution 하는 연구들이 많이 진행되고 있답니다.😊

Laplacian Image Pyramid

앞에서 공부하였던 Downsampling에서 우리는 픽셀을 없애기 전 먼저 Gaussian 을 적용해주었습니다. 이 값을 원본 이미지에서 뺀다면 위와 같은 결과가 나오게 됩니다. 그래서 색이 균일한 영역은 값의 차이가 거의 없어 색이 두드러지지 않지만 그렇지 않은 부분은 값의 차이가 위의 결과와 같이 두드러지게 됩니다. 그리고 우리는 이 결과를 Residual 이라고 합니다. 결국 Downsampling을 하게 되면 이 Residual만큼의 정보 손실이 일어나게 되는 겁니다.

우리가 이번 주제에서 공부할 Laplacian Image Pyramid 는 특이하게도 이전 Gaussian Image Pyramid 가 blur된 이미지를 저장하는 것과 반대로 이 Residual 값을 저장합니다.

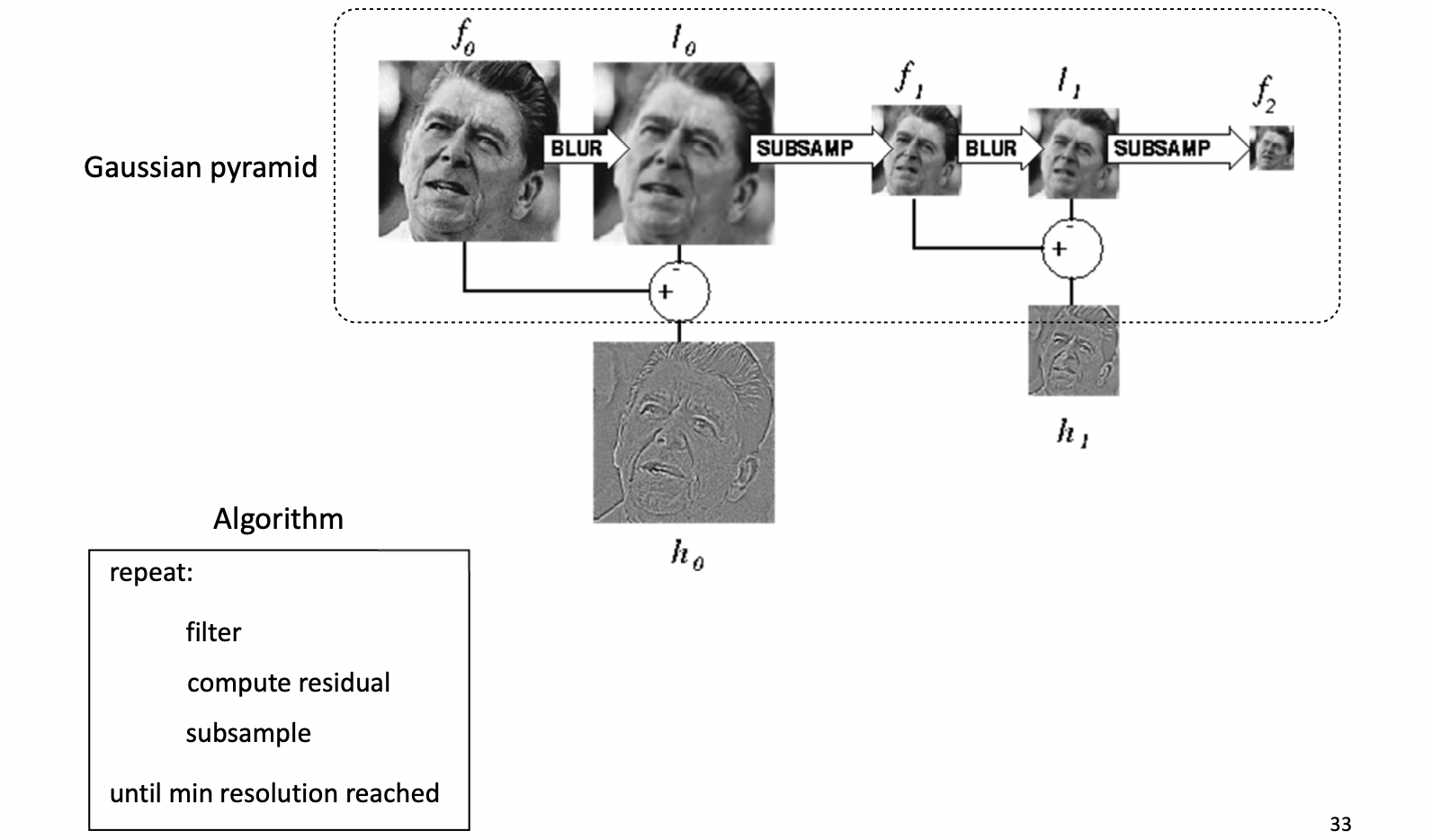
이전 Gaussian Pyramid 는 위와 같은 과정에서 $f_0, f_1, f_2$ 를 저장한 데 반해, Laplacian Pyramid 는 $h_0, h_1, f_2$ 를 저장합니다. 이 Residual을 이용해서 Laplacian Pyramid 는 원본 이미지로 Reconstruction 하는 것이 가능합니다.

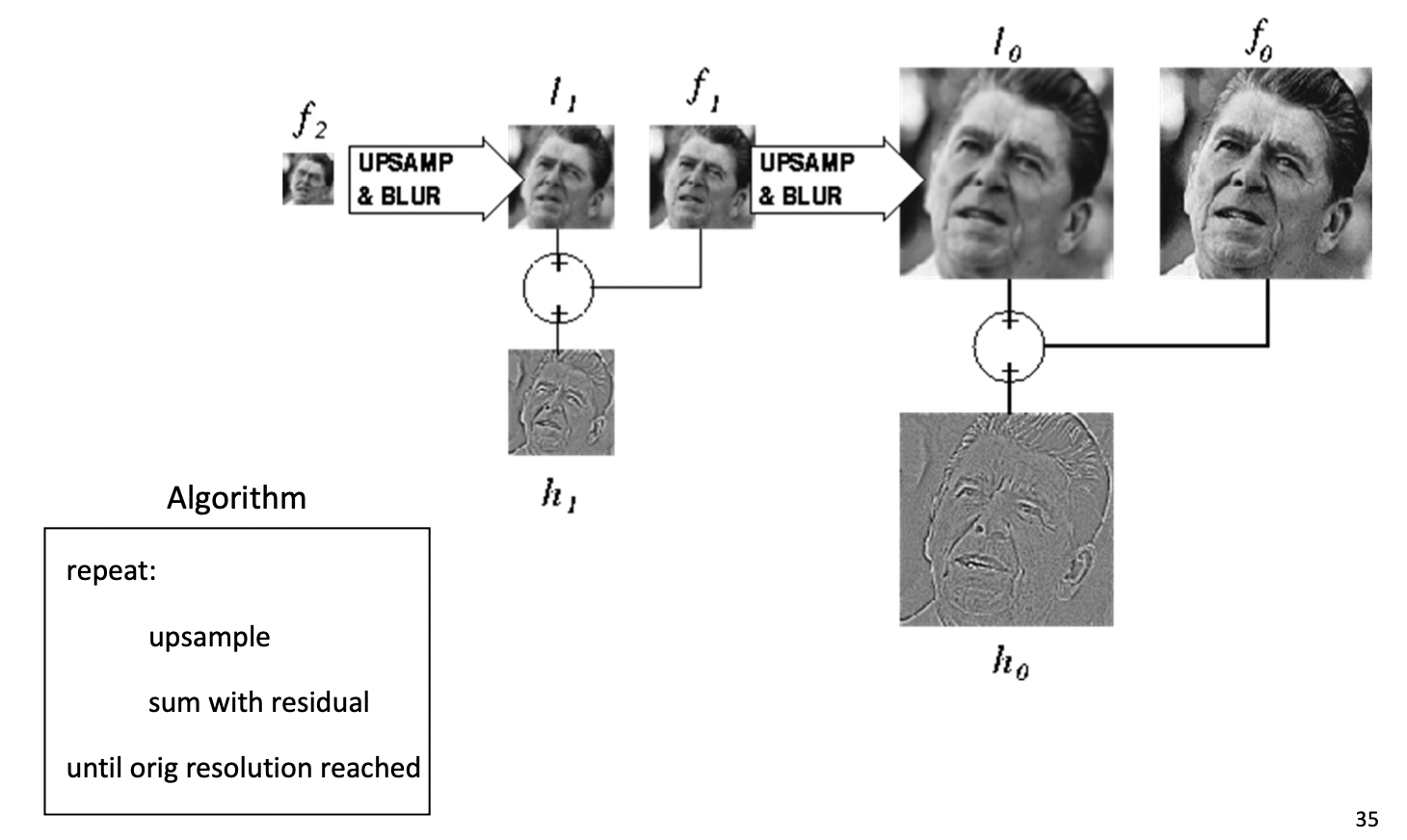
먼저, 기본 이미지를 Upsampling 해줍니다. 간단하게 픽셀의 행과 열을 2배로 늘려주고 0으로 채워주는 Zero Insertion을 수행합니다. 2배로 쭈욱 늘려준다는 뜻은 기존의 픽셀 값들의 좌표 또한 2배가 된다는 뜻입니다. 기존 (1, 1)이 었던 픽셀의 값은 (2, 2)에 저장된다는 뜻이지요. 예시를 확인하면 아래와 같습니다.

$\begin{bmatrix} 1 \ 6 \\ 8 \ 3 \end{bmatrix}\rightarrow\begin{bmatrix} 1\ 0\ 6\ 0\\ 0\ 0\ 0\ 0 \\8\ 0\ 3\ 0\\ 0\ 0\ 0\ 0 \end{bmatrix}$

이후에 이 이미지를 blur 처리한다면 기존에 있는 픽셀 값들이 주변으로 퍼져나가 0 인 값들을 채우게 됩니다. 이렇게 blur 된 이미지에 저장하고 있던 Residual 을 더함으로써 기존의 이미지로 Reconstruction 을 할 수 있습니다. upsampling 후 blur를 하는 이 방식이 blur 후 downsampling을 하는 Gaussian Pyramid의 방식과 완전히 역순으로 흘러가는 것을 확인할 수 있습니다.

그렇다면 왜 우리는 이것을 Laplacian 이라 부를까요? 우리가 기존의 알고있던 Laplcian은 Gaussian을 두 번 미분한 이계도함수 였습니다.

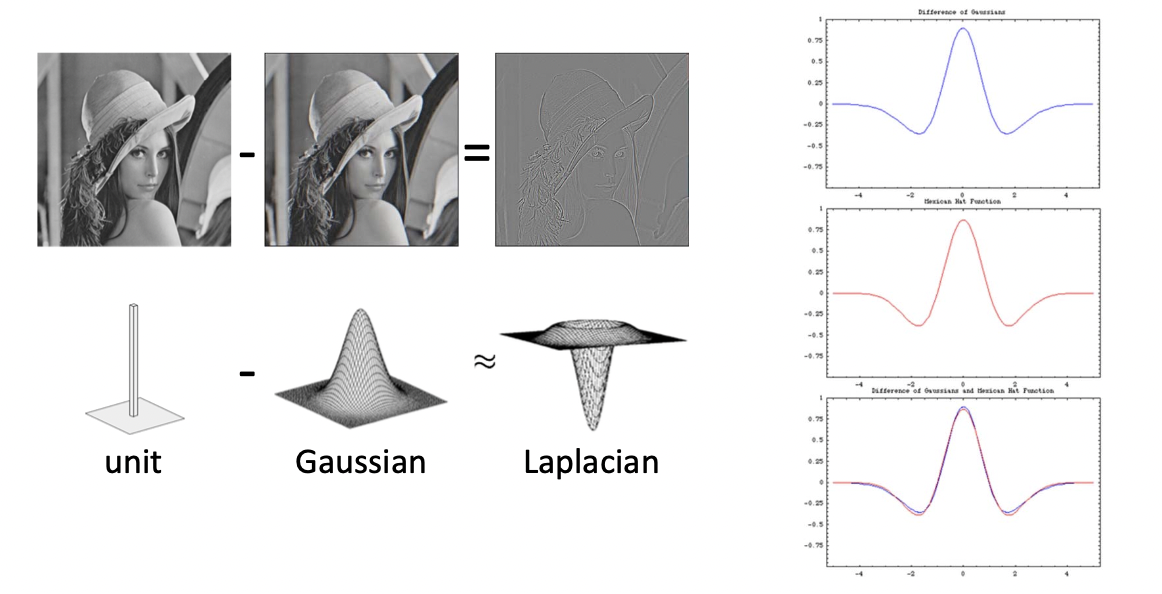
그런데 원본에서 Gaussian을 뺀 이 Residual 이라는 값의 생김새가 실제로 Laplacian과 굉장히 유사한 모양을 하고 있기 때문에 Laplacian Pyramid 라고 부르는 거랍니다.😂

그렇다면 원초적으로, 우리는 대체 왜 Laplacian Pyramid 를 사용하는 것일까요?

위의 그림에서 Gaussian Pyramid 와 Laplacian Pyramid 를 보면 알 수 있겠지만 두 피라미드 모두 원본 이미지의 33%만이 추가적인 메모리로 사용되는 것을 알 수 있습니다. 그런데 결론부터 얘기하자면 Laplacian Pyramid 는 Compression(압축)에 활용될 수 있기 때문에 일반적으로 더 적은 메모리를 필요로 하게끔 디자인할 수 있습니다. 왜 그럴까요?

우리가 일반적으로 RGB를 표현할 때는 보통 0 ~ 255 까지의 값을 표현하기 위해 8비트 를 사용합니다. 그런데 Residual 을 생각해봅시다. 원본 값에서 원본 값을 최대로 한 평균을 빼는 것이 범위가 그렇게 클까요? 그렇지 않을 겁니다. 그래서 0~31까지의 5비트 정도면 충분할 수 있는 것이죠. 그렇게 되면 메모리 상으로 무려 $\frac{3}{8}$인 37.5%를 추가적으로 절약할 수 있습니다. 이 예시의 경우로 계산을 해보면 $\frac{4}{3}\times\frac{3}{8} = \frac{5}{6}$ 이므로 심지어 원본값보다 적은 메모리만을 사용하게 됩니다. 더 적은 메모리로 원본을 복원할 수 있다는 점 때문에 앞서 말했듯이 Image Compression(이미지 압축) 에 사용될 수 있는 것입니다.