저번 시간의 Image Gradient 에 이어 이번 시간에는 물체의 모서리를 찾는 Corner Detection 을 알아보도록 하시죠.

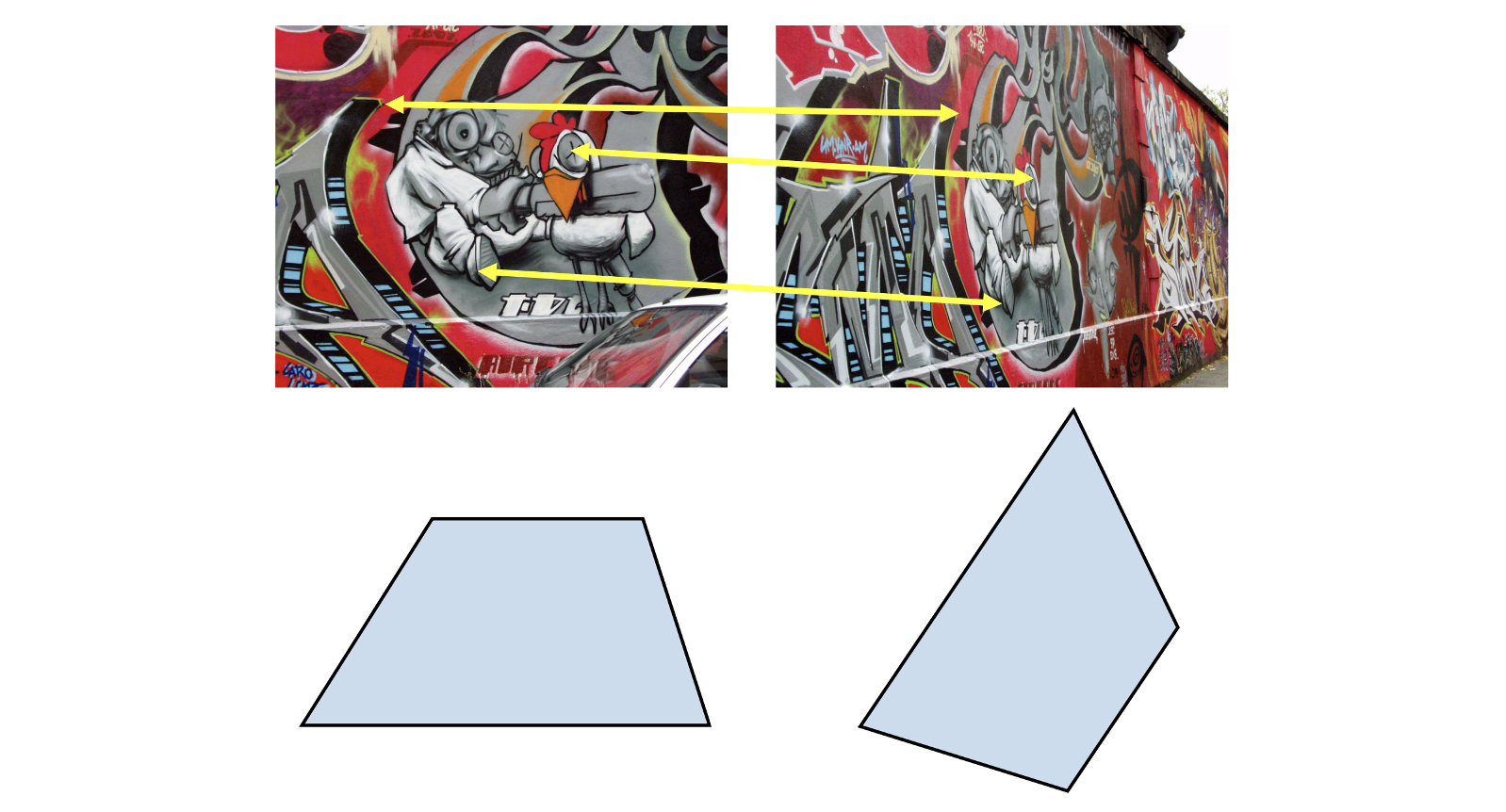
가장 먼저, Corner 를 찾는 것이 왜 중요할까요? 아래 그림의 왼쪽과 같이 책에 대한 이미지가 있다고 합시다. 그리고 이 정보를 통해 오른쪽의 이미지에서 해당하는 책을 매칭할 때 Corner 정보가 사용됩니다. 이와 같이 책의 표지는 2차원 평면에 해당하기 때문에 이와 같은 작업을 Planar Object Instance Recognition 이라고 합니다.

2차원이 있으면 3차원의 Object Recognition 도 있을 겁니다. 이때도 마찬가지로 Corner들끼리 비교를 했을 때 상당히 높은 정확도로 이미지 매칭을 할 수 있습니다.

로봇들이 현재 자신이 건물 안의 어디 있는지를 분별하기 위해서는 천장의 형광등, 문과 같은 정적인 객체들을 기준으로 합니다. 이럴 때도 Corner가 상당히 중요한 feature이 되어줍니다. Corner를 매칭하기 전에 선행되어야 할 것이 바로 그 Corner들이 도대체 어디에 있는가이며, 이것이 이번 주제인 Corner Detection 이라 할 수 있겠습니다.

아래와 같은 그림들은 모두 우리가 판단하기에는 같은 모양을 띄고 있지만, 각도가 달라 완전히 같은 이미지라고는 할 수가 없습니다. 컴퓨터는 이 때 Corner들을 찾아 비교 및 매핑합니다.

Corner가 중요하단 얘기는 이 만큼 했으면 차고 넘치는 것 같습니다. 이제 본격적으로 Corner Detection 을 어떻게 할 지에 대해서 얘기해보도록 하죠.

Visualizing Quadratics

Corner Detection 얘기를 시작하기 전에 우리가 먼저 알아야할 것이 바로 Visualizaing Quadratics, 즉 2차식을 시각화하는 작업입니다.

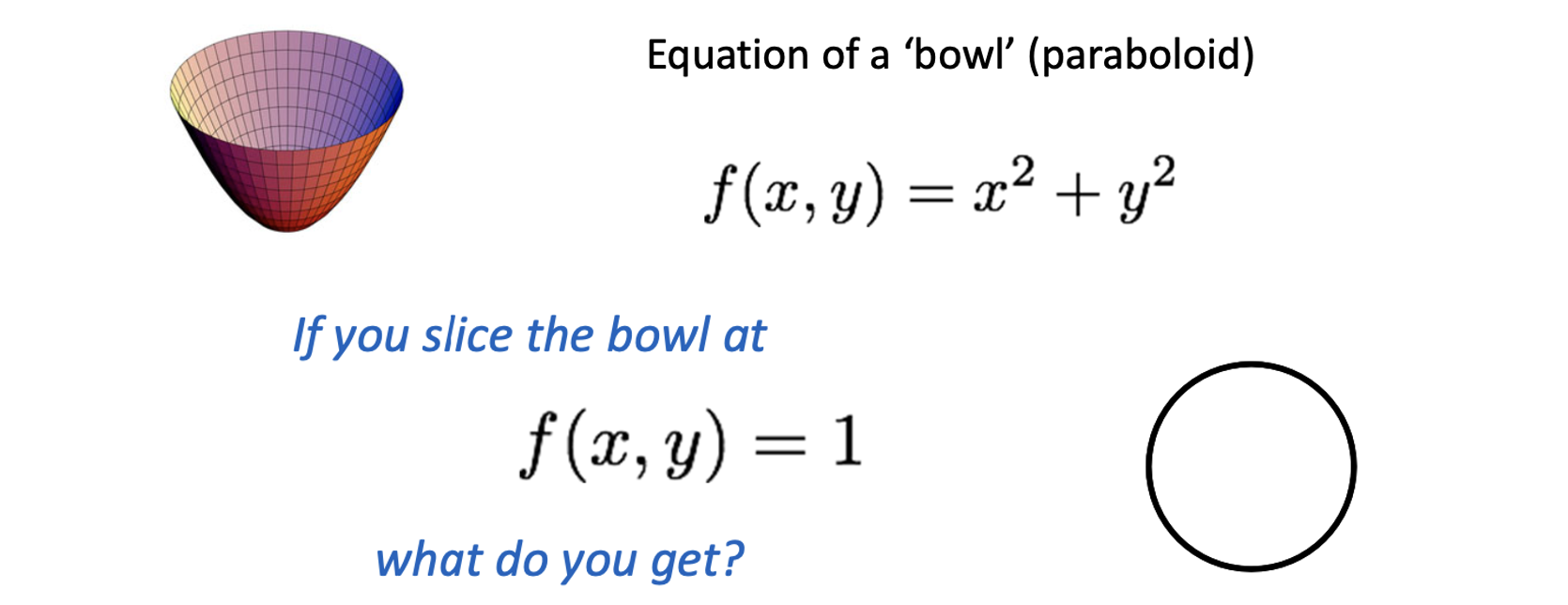
우리는 이미 $x^2 + y^2 = r^2$은 반지름이 r인 원이라는 것을 알고 있습니다. 그렇다면 $x^2 + y^2 = z$는 3차원으로 표현하면 어떤 모양일까요? 위의 그림과 같이 그릇을 모양을 하고 있는데 이를 우리는 Paraboloid 라고 합니다. 이 Paraboloid를 $z$가 1인 지점에서 $xy$ 평면으로 자른다면 위와 같이 반지름이 1인 원이 나올 겁니다. 마찬가지로 $r^2$에서 자른다면 반지름이 $r$인 원이 되겠지요.

이 $f(x,y)$를 matrix로 나타낸 것은 아래와 같습니다.

$f(x,y) = x^2+y^2=\begin{bmatrix}x\quad y\end{bmatrix}\begin{bmatrix}1\quad0\\0\quad1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$

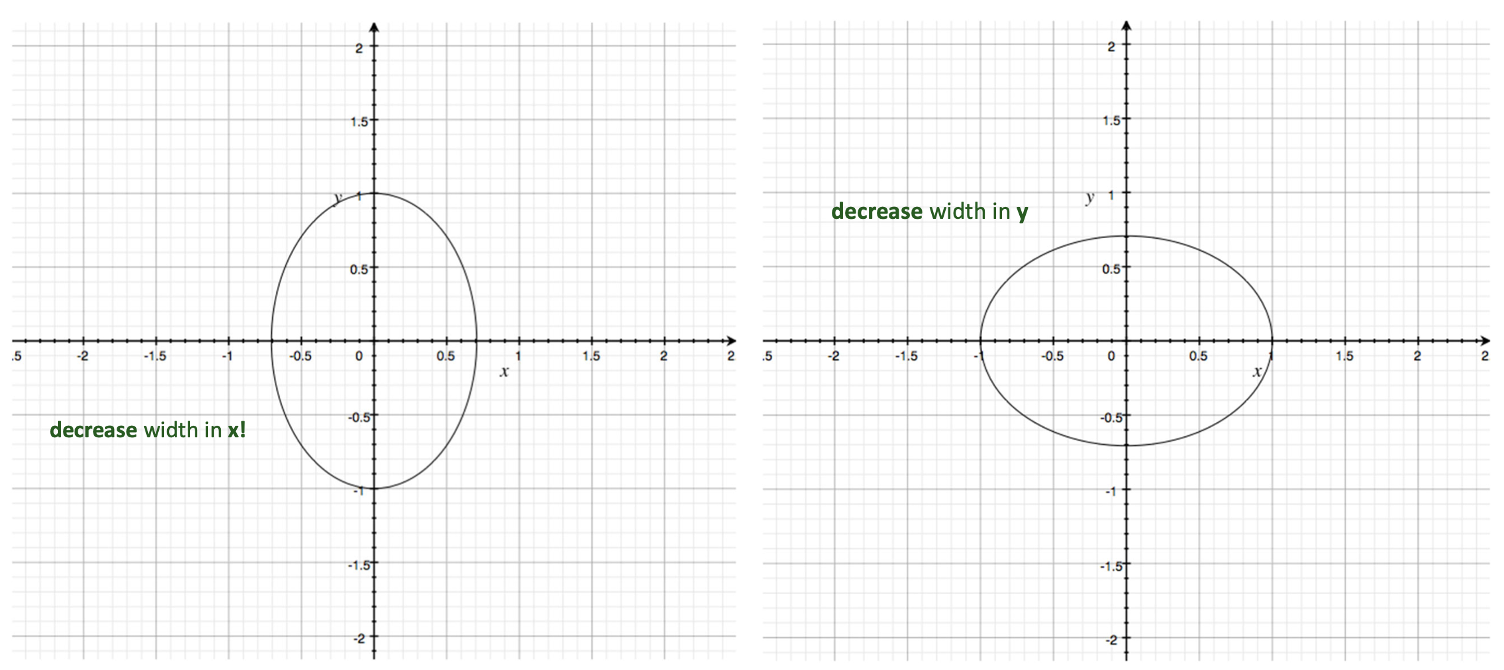
그렇다면 만약에 우리가 가운데에 있는 matrix를 일부 수정해 $f(x,y) =\begin{bmatrix}x\quad y\end{bmatrix}\begin{bmatrix}2\quad0\\0\quad1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$와 같이 바꾸면 어떻게 될까요? 결과는 $f(x,y)$를 1에서 자른다면 $2x^2 + y^2= 1$이라는 식이 나오고 이는 Ellipse(타원)의 방정식임을 알 수 있습니다. $x^2+y^2=1$이라는 원에서 x축의 너비가 작아진, 아래 그림의 왼쪽과 같은 형태가 됩니다. 비슷하게 $f(x,y) =\begin{bmatrix}x\quad y\end{bmatrix}\begin{bmatrix}1\quad0\\0\quad2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$와 같이 바꾼다면 오른쪽과 같은 형태가 나오게 되는 것이죠.

다시 돌아와서 그럼 우리 이제 $f(x,y) = x^2+y^2=\begin{bmatrix}x\quad y\end{bmatrix}\begin{bmatrix}1\quad0\\0\quad1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$ 식에서 가운데의 matrix인 $\begin{bmatrix}1\quad0\\0\quad1\end{bmatrix}$에 Singular Value Decomposition(SVD)를 적용해보자 이겁니다. 결과는 아래 그림과 같습니다.

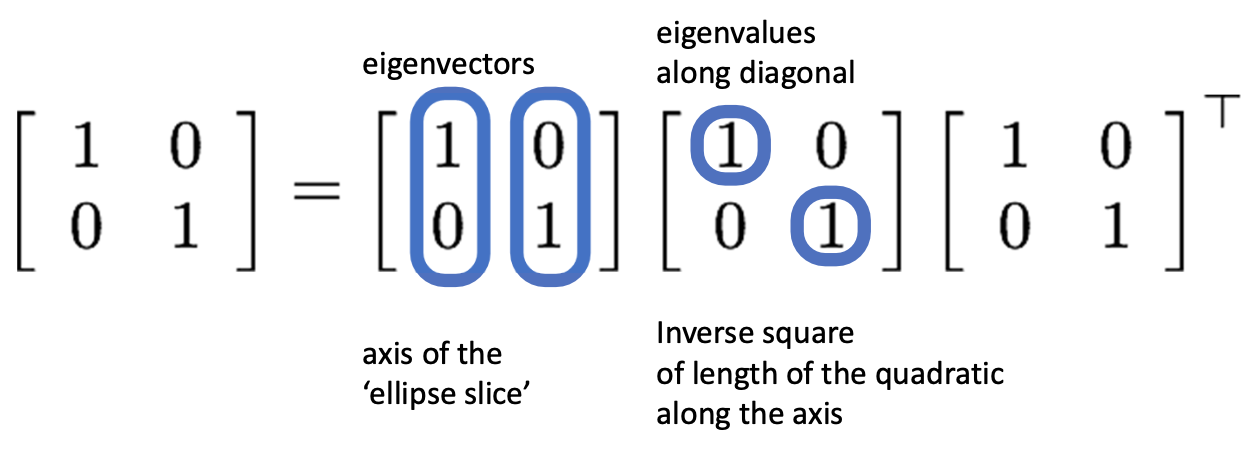
첫 번째 matrix에 있는 두 개의 값들이 바로 eigenvector이며, 가운데 matrix의 대각선에 위치한 값들이 바로 eigenvalue가 되겠습니다. 이것들을 우리가 지금까지 논의를 했던 Paraboloid 에 기하학적으로 해석을 해봅시다. 그렇게 되면 eigenvector 는 우리가 Paraboloid를 슬라이스한 Ellipse(타원)의 두 축이 되고, eigenvalue는 그 타원의 긴 반지름, 작은 반지름의 역수가 됩니다. 우리가 이것을 통해 알아야 할 것은 $f(x,y)$의 가운데 matrix가 그릇의 형태를 결정짓기 때문에, 우리가 이를 잘랐을 때의 모양도 이 matrix가 관할하게 된다는 것입니다.

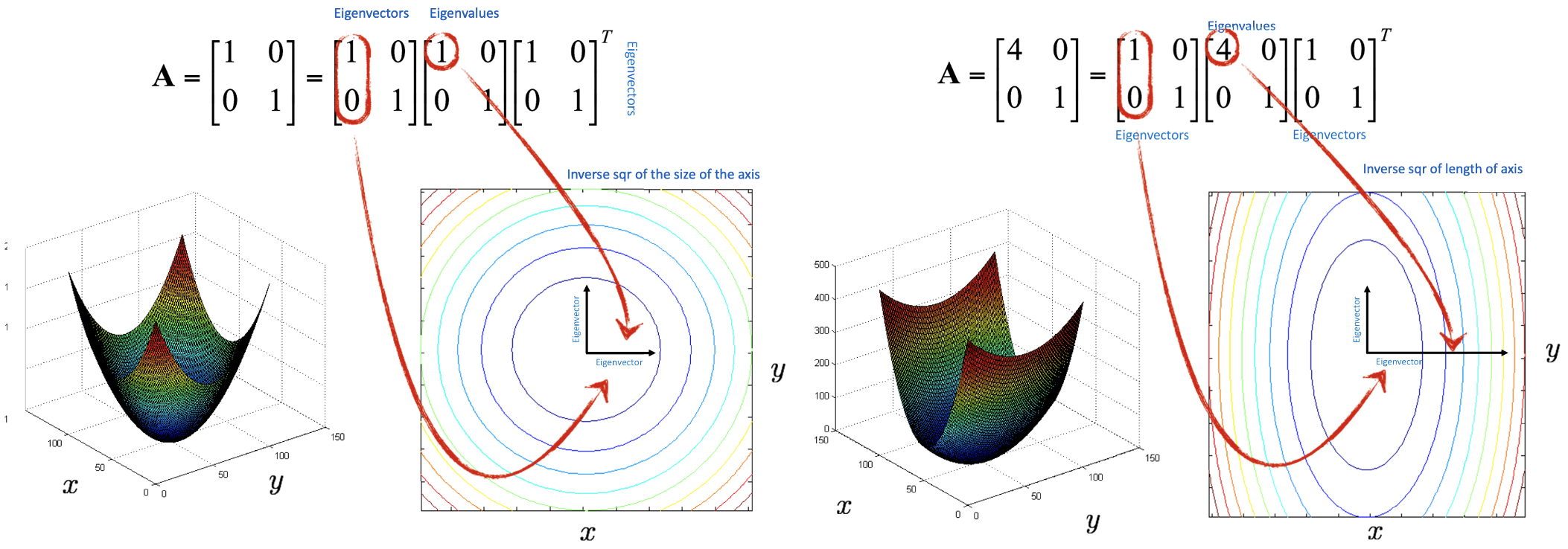
위의 그림에서 오른쪽의 첫 번째 eigenvalue가 4이기 때문에 $x$ 축에 대한 반지름이 $\frac{1}{\sqrt{4}}=\frac{1}{2}$므로 $y$축에 대한 긴 반지름이 2배가 되는 타원 형태가 되는 것입니다. 아래와 같은 복잡한 경우는 어떨까요?

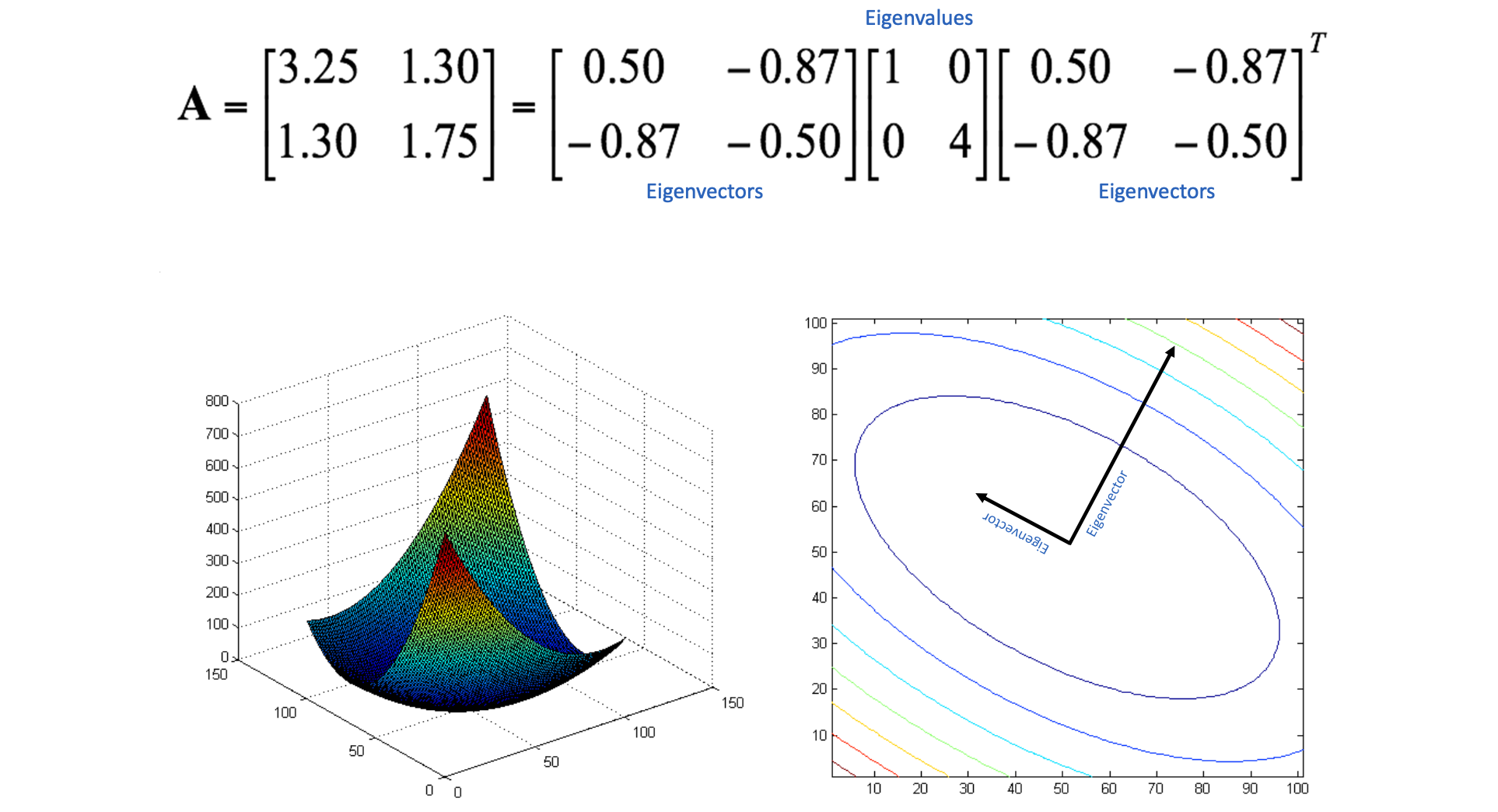
위와 같은 경우를 전개하면 $f(x,y)=3.25x^2 +1.30xy+1.30xy+1.75y^2$이며, $xy$에 대한 식이 존재합니다. 그렇기 때문에 이 Paraboloid를 슬라이스 한다면 오른쪽과 같이 돌아가있는 형태의 타원이 나오게 됩니다. $\begin{bmatrix}0.50\\ -0.87\end{bmatrix}$ 벡터를 축으로 하는 반지름은 $1$, $\begin{bmatrix}-0.87\\ -0.50\end{bmatrix}$벡터를 축으로 하는 반지름은 $\frac{1}{\sqrt{4}}=\frac{1}{2}$의 비율을 가지는 타원이 되는 것입니다. (그림이 완전 정확하지는 않습니다😅)

Harris Corner Detector

지금까지 간단한 수학을 짚고 넘어간 이유는 앞으로 공부할 이 Harris Corner Detector를 위해서 였습니다.

Harris Corner Detector 가 하고자 하는 것은 무엇일까요?

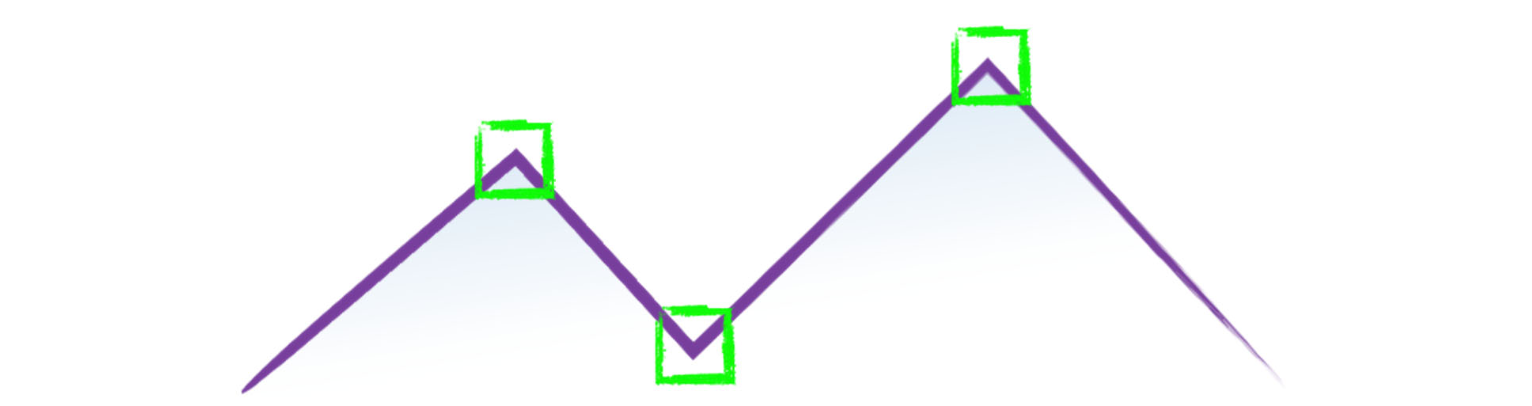
위 그림을 보면 Corner 가 3개인 것을 확인할 수 있습니다. 이 Corner를 찾는 것은 우리가 위와 같은 녹색 윈도우를 Shift 하다가 이것이 Corner다! 하는 경우 이야기를 하도록 알고리즘이 이루어집니다. 그렇기 때문에 input으로는 Small Image Patch 즉 윈도우에 해당하는 작은 이미지 영역이 될 것이고 output으로는 그것이 Corner인지 아닌지 혹은 Corner인 정도를 나타내는 연속적인 수치가 됩니다.

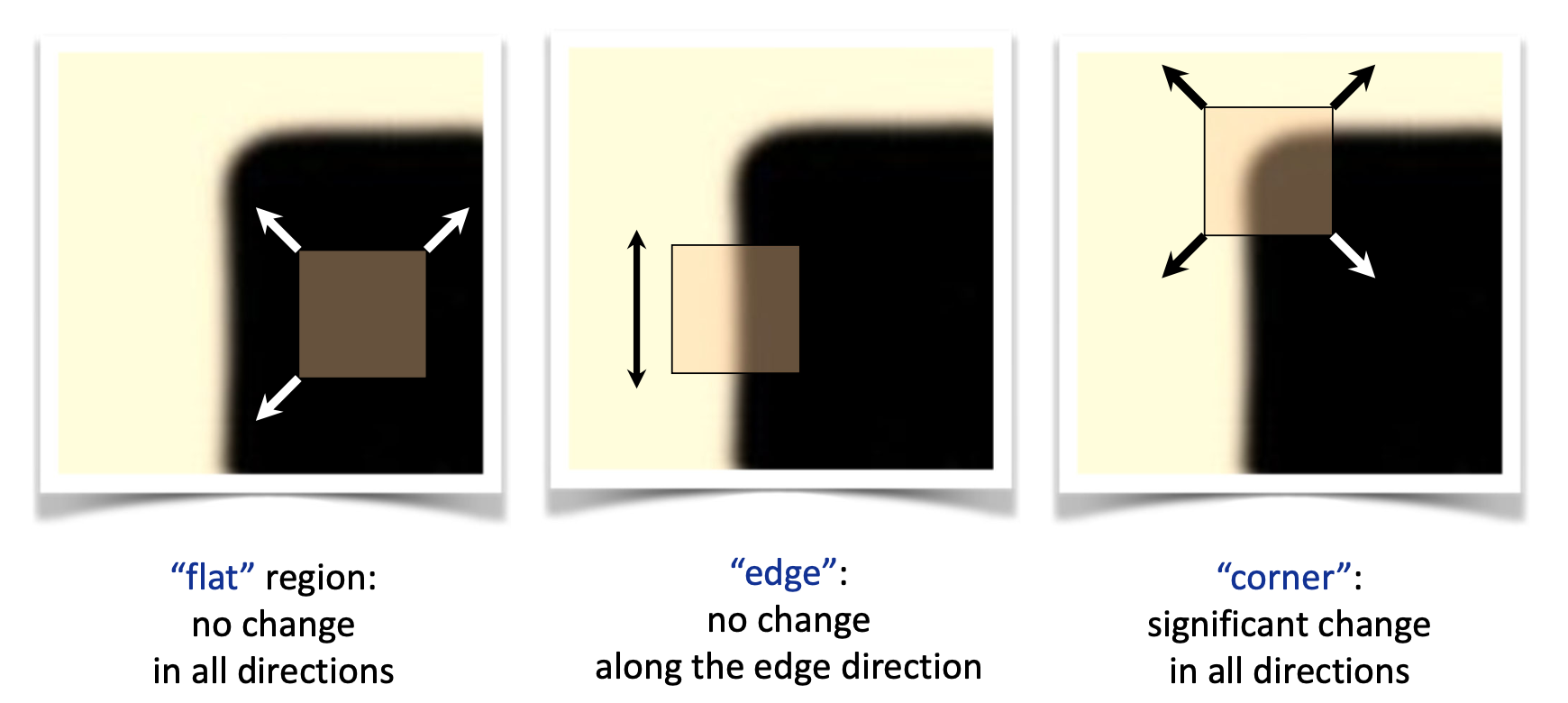
위 그림의 가장 왼쪽을 봅시다. 저 위치에서의 윈도우는 어떤 방향이든 윈도우를 살짝 움직인다 하더라도 색상에 변화가 없습니다. 전부 검정색이죠. 그렇기 때에 이 영역은 flat 한 영역이라고 할 수 있습니다. 이어서 가운데 그림을 봅시다. 이렇게 윈도우를 edge 영역에 놓았을 경우 해당 윈도우를 좌우로 edge에 수직으로 움직이는 것은 제법 많은 영역의 색상 변화를 불러 일으킵니다. 그러나 위 아래로 edge를 따라서 움직일 경우에는 색상 변화가 없습니다. 마지막으로 corner 를 보면 어떤 방향으로 움직이더라도 상당히 많은 픽셀 값들의 변화가 이루어집니다.

Harris Corenr Detector 가 Corner Detection 을 수행하는 과정을 순서대로 나타내면 아래와 같습니다.

1. Compute image gradients over small region
2. Subtract mean from each image gradient
3. Compute the covariance matrix
4. Compute eigenvectors and eigenvalues
5. Use threshold on eigenvalues to detect corners

이 과정들을 하나씩 찬찬히 살펴보도록 합시다.

1. Compute image gradients over small region

위와 같이 이미지 패치(예시에서는 5 x 5)를 이용해서 각기 다른 형태의 이미지에 대하여 derivative 를 수행한 결과는 이와 같습니다. 가장 오른쪽의 Corner 결과를 보시면 딱 모서리에 해당하는 곳에서 X derivative 와 Y derivative 가 모두 큰 것을 확인하실 수 있습니다. 그래프로 표현한 것은 아래와 같습니다.

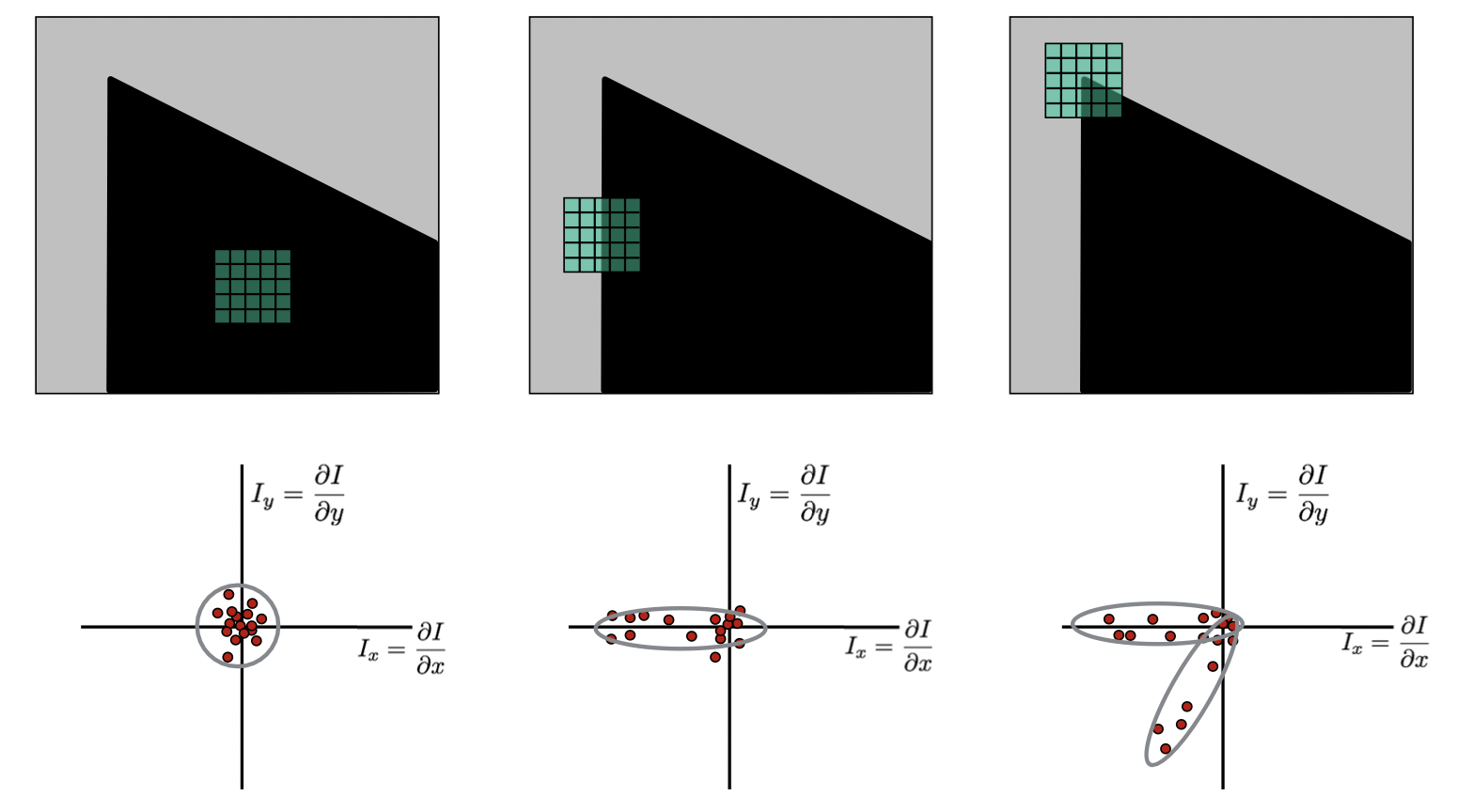
먼저 가장 왼쪽 flat 영역을 보시면 $I_x$와 $I_y$가 모두 작기 때문에 위와 같이 원점에 오밀조밀한 형태가 만들어지게 됩니다. 가운데와 같이 edge 인 곳에서는 $I_x$ 의 절댓값이 크고, $I_y$ 는 작기 때문에 위와 같이 한 쪽 방향으로 분포하는 형태가 됩니다. 그리고 마지막으로 corner 를 봅시다. 패치 내에 검정 영역이 수직으로 되어 있는 부분에 대해서는 edge 영역과 같이 나옵니다. 그러면 대각으로 떨어지는 영역을 봅시다. 이 곳에서는 $I_x$ 와 $I_y$ 가 모두 어느 정도 절댓값을 같기 때문에 좌표에 대각선으로 분포하게 됩니다. 즉, corner에서는 두 개로 쪼개져 분포하는 모습을 보이는 것이죠. 그런데 컴퓨터는 인간과 같이 그래프를 보고 판단하는 게 아니잖아요? 계속 보시죠.

2. Subtract the mean from each image gradient

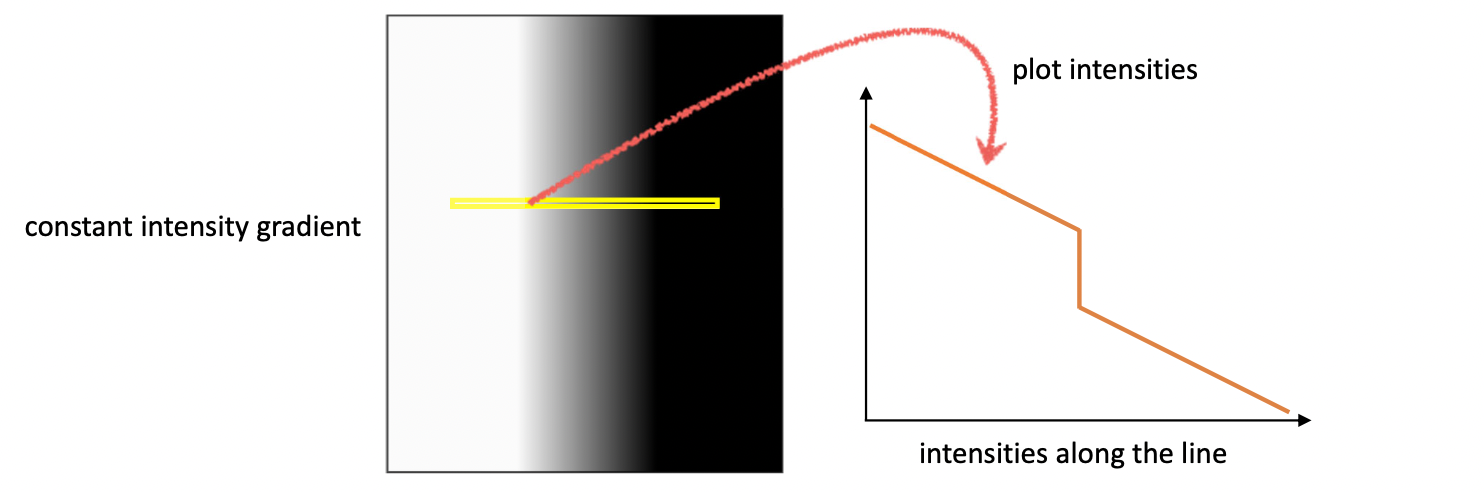
실제로 이미지의 edge 영역을 더 가까이 관찰하게 되면 대부분 어쩔 수 없이 edge 를 기점으로 양쪽에 그라데이션이 형성되어 있기 마련입니다. 정말 이상적으로 edge 양쪽으로 색상이 딱! 하고 바뀌기는 쉽지 않죠. 즉, 위와 같은 Intensity 그래프에서 값이 급격히 바뀌는, 기울기가 큰 부분이 진정한 edge 라고 할 수 있습니다. edge 양쪽으로도 기울기가 존재하기에 edge 라고 생각하게 될 수 있지만 실제로는 그 값이 매우 작은 그라데이션 영역인 겁니다.

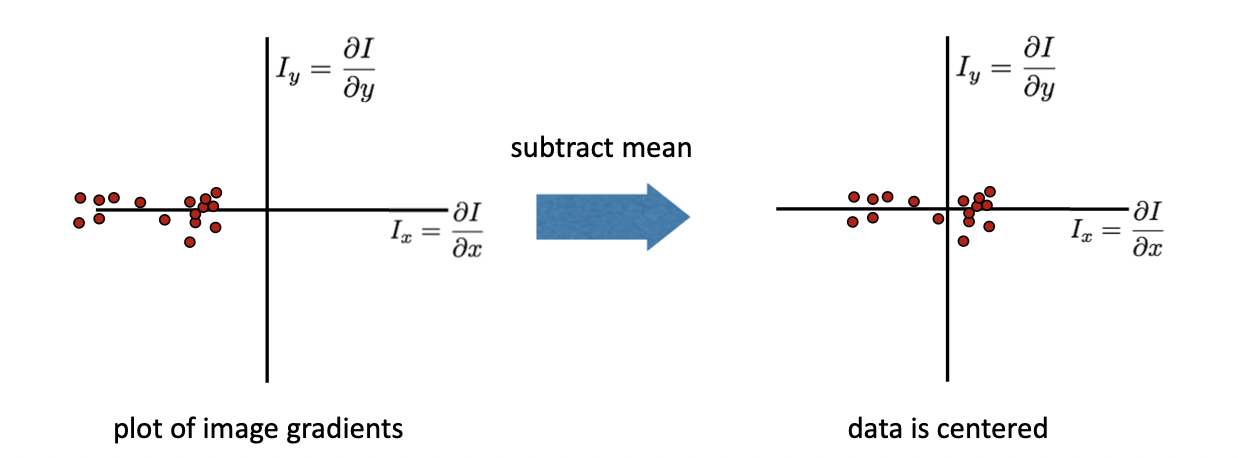
마찬가지로 전체적으로 기울기가 어느 정도 존재하기 때문에 위 그림의 왼쪽 그래프와 같이 분포가 왼쪽으로 편향되어 있는 것을 확인할 수 있습니다. 이 값을 보정하기 위해서 우리는 값들의 평균을 빼주는 작업을 합니다. 그렇다면 값들이 전체적으로 원점을 기준으로 평행 이동하게 되는 것이지요. 이를 Zero Centering 이라고도 부릅니다.

3. Compute the covariance matrix

먼저 Covariance Matrix은 아래와 같은 행렬을 의미합니다.

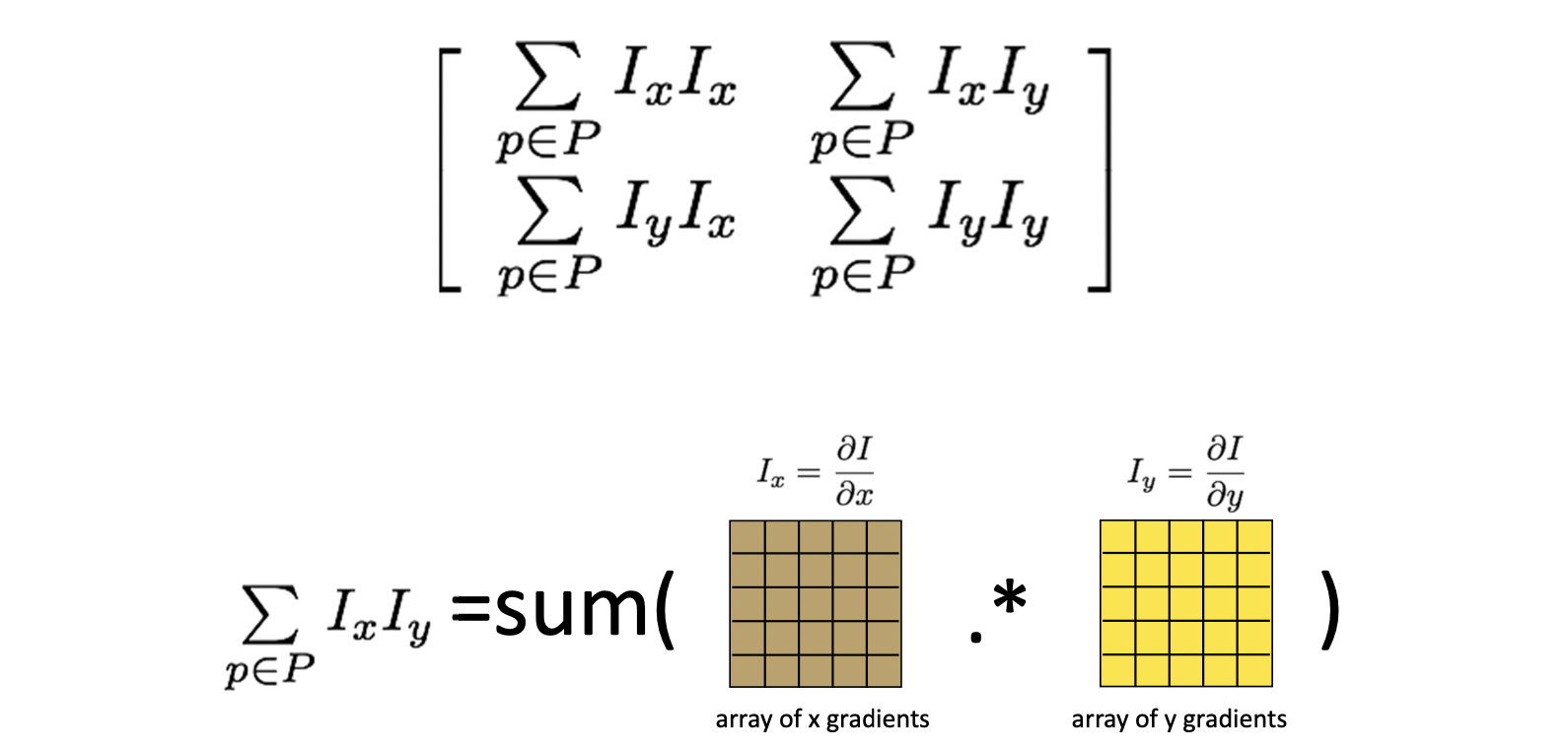
여기서 먼저, $I_xI_y$는 $I_x$와 $I_y$의 요소별 곱(.*)을 의미합니다. 말 그대로 크기가 같은 두 행렬의 같은 위치에 있는 요소 둘을 곱하여 똑같은 크기의 행렬을 만드는 과정입니다. 곱한 다음에는 그 모든 요소들을 다 더합니다. 예시로 $I_x$가 $\begin{bmatrix}a\ b\ c\ d\ e\\f\ g\ h\ i\ j\ k\\...\end{bmatrix}$와 같은 형태라면 $\sum_{p\in P}I_xI_x = a^2 + b^2 + c^2 + d^2 + e^2 + f^2 + g^2 + ...$이 되는 겁니다. 여기서 $\sum_{p\in P}I_xI_y$와 $\sum_{p\in P}I_yI_x$는 같기 때문에 위와 같은 Covariance Matrix 는 대칭 구조를 가지는 Symmetric Matrix 라는 특징이 있습니다.

말 그대로 Covariance 이기 때문에 어떤 하나가 변할 때, 즉 $x$ 축이 변할 때 $y$ 축이 얼마나 변하는지를 나타내주는 행렬이 바로 Covariance Matrix이게 되는 겁니다. 이를 이용해서 flat, edge, corner 를 설명할 수 있겠다 한 것이 바로 아이디어 입니다.

다시 돌아와, 그럼 우리는 이 윈도우를 $(u,v)$ 만큼 움직였을 때 얼마나 달라지는 지 Error Function 을 정의하고 싶어집니다. 어떤 위치에서의 Intensity를 $I(x,y)$라고 표현한다면($I_x, I_y$ 와 헷갈리시면 안됩니다😅) Error Function의 정의는 아래와 같습니다.

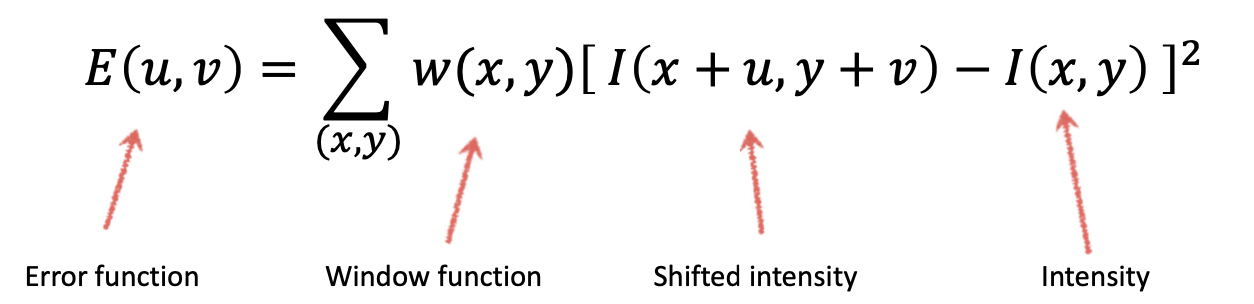
먼저 $[I(x+u,y+v)-I(x,y)]^2$는 이미지를 $(u,v)$ 만큼 평행이동한 값과 원래의 값을 빼어주어 곱하는 식입니다. 이를 통해 둘의 차를 절댓값으로 나타낼 수 있죠. 이 식은 이미지의 전체 영역에 대하여 계산하기 때문에 우리의 윈도우 영역으로 이를 한정해주는 함수가 필요한 데 이것이 바로 Window Function 입니다. 아래와 같이 Window 영역에서만 1이고, 나머지 부분을 0으로 하여 Window 부분만만 고려할 수도 있고 오른쪽과 같이 Gaussian 을 적용할 수도 있는 것이죠. 변하지 않는 건 Window 에서의 값을 추출하기 위한 함수라는 점입니다.

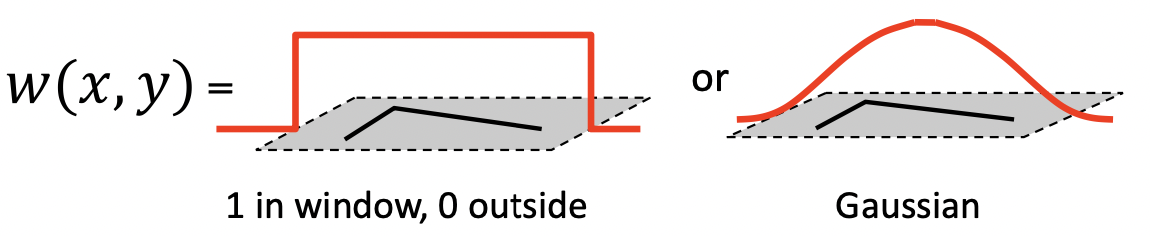
우리가 고려해야 될 부분은 움직이고자 하는 $u$ 와 $v$ 가 매우매우 작다는 점입니다. 이 점을 이용하면 아래처럼 $I(x+u,y+v)$ 를 approximation 할 수 있습니다.

$I(x+u,y+v) \approx I(x,y) + I_xu + I_yv$

이를 대입해서 Error Function 을 다시 쓴다면, 아래와 같이 quadratic equation(이차방정식)이 나옵니다.

$E(u,v) = u^2\sum_{(x,y)}w(x,y)I_x^2 + 2uv\sum_{(x,y)}w(x,y)I_xI_y + v^2\sum_{(x,y)}w(x,y)I_y^2$

무언가 익숙한 모양이죠? 이를 Matrix 에 대한 식으로 정리하면 아래와 같습니다.

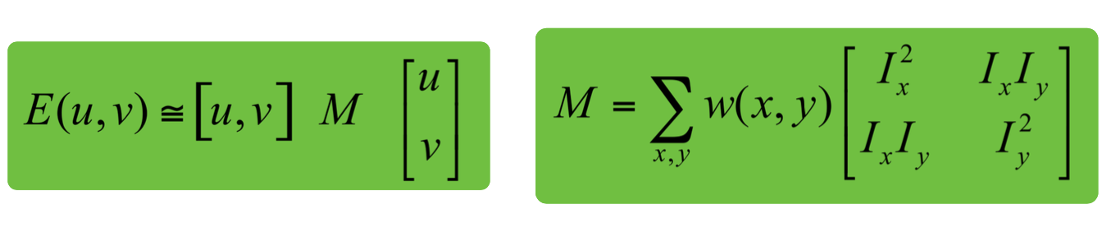
$M$에서 우리는 아까 공부하였던 Covariance Matrix 를 확인할 수 있습니다. 이 $M$과 같은 matrix를 우리는 second moment matrix 혹은 structure tensor 라고 부릅니다. 이렇게 되면 우리는 $u, v, E(u,v)$ 를 축으로 하는 3차원 Surface 를 수 있고 우리는 이 생김새를 보고 flat 인지, edge 인지, corner 인지를 판단하고자 합니다. 물론 그 생김새에 영향을 주는 것은 matrix $M$ 이겠죠?

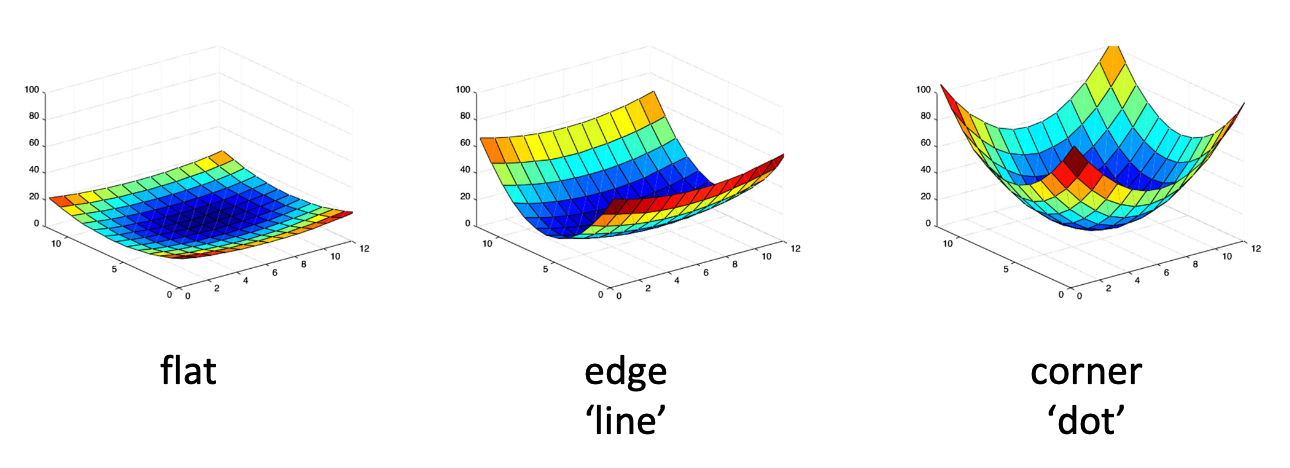
Visualization한 결과는 위와 같습니다. 느낌이 오시죠? 가장 왼쪽은 $u$축, $v$ 축 모두 움직여도 $E(u,v)$에 큰 변화가 없습니다. flat 영역입니다. 가운데는 $v$ 축으로 이동하면 값의 변화가 크지만 $v$ 축으로는 이동하여도 높의 변화가 거의 없습니다. edge 영역인 겁니다. 마지막 가장 오른쪽 그림은 어디로라도 값의 변화가 크기 때문에 corner가 되는 겁니다.

하지만, 다시 말하지만 컴퓨터는 Visualization 의 결과를 보고 판단하지 않습니다. 그래서 우리는 오직 수치로 이를 이해하려 합니다.

4.Compute eigenvalues and eigenvectors

그래서 우리가 활용하고자 하는 것이 바로 eigenvector(고유벡터)와 eigenvalue(고유값) 입니다. 정확히는 우리는 방향이 아닌 변화량을 알고 싶기 때문에 eigenvalue 에 더 초점을 맞추고자 합니다. 먼저, 정의는 아래와 같습니다.

$Me = \lambda e$ 일 때 $e$는 eigenvector, $\lambda$는 eigenvalue

그런데 여기서, $M=\sum\begin{bmatrix}I_x^2\quad I_xI_y\\I_xI_y \quad I_y^2 \end{bmatrix}$($w$는 생략) 이므로 이는 $2 \times 2$ 크기를 가지는 Symmetric matrix 입니다. 그렇기 때문에 이 $M$을 SVD 한다면 항상 아래와 같은 형식이 나오게 됩니다.

$M = R^{-1}\begin{bmatrix}\lambda_1 \quad 0 \\ 0 \quad \lambda_2\end{bmatrix}R$

그리고 여기서 $\lambda_1$과 $\lambda_2$ 는 모두 eigenvalue 를 의미하게 됩니다. 그렇게 되면 $M$은 아래와 같이 $R$을 축으로, $\lambda$를 반지름으로 하는 하나의 타원으로 표현할 수 있게 됩니다.

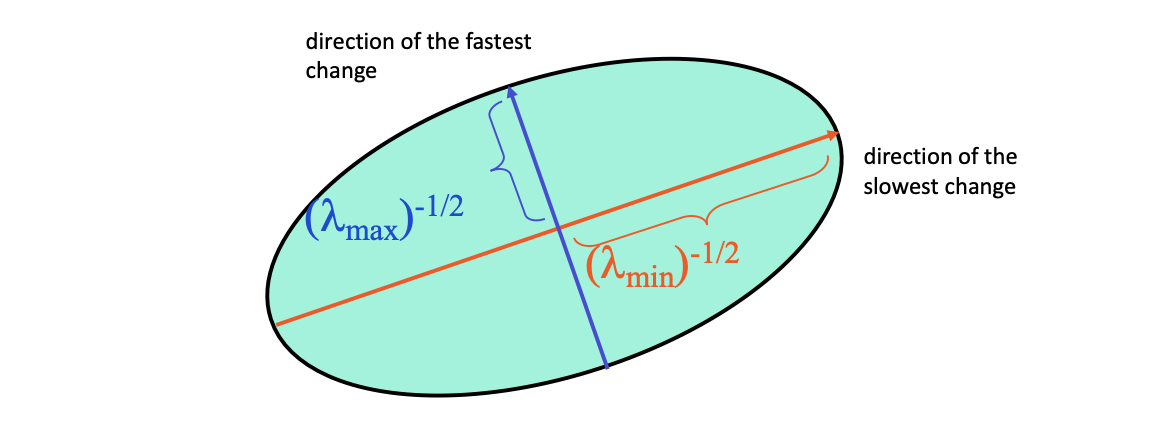
이 $\lambda_1$와 $\lambda_2$ 값을 펼쳐보면 아래와 같습니다.

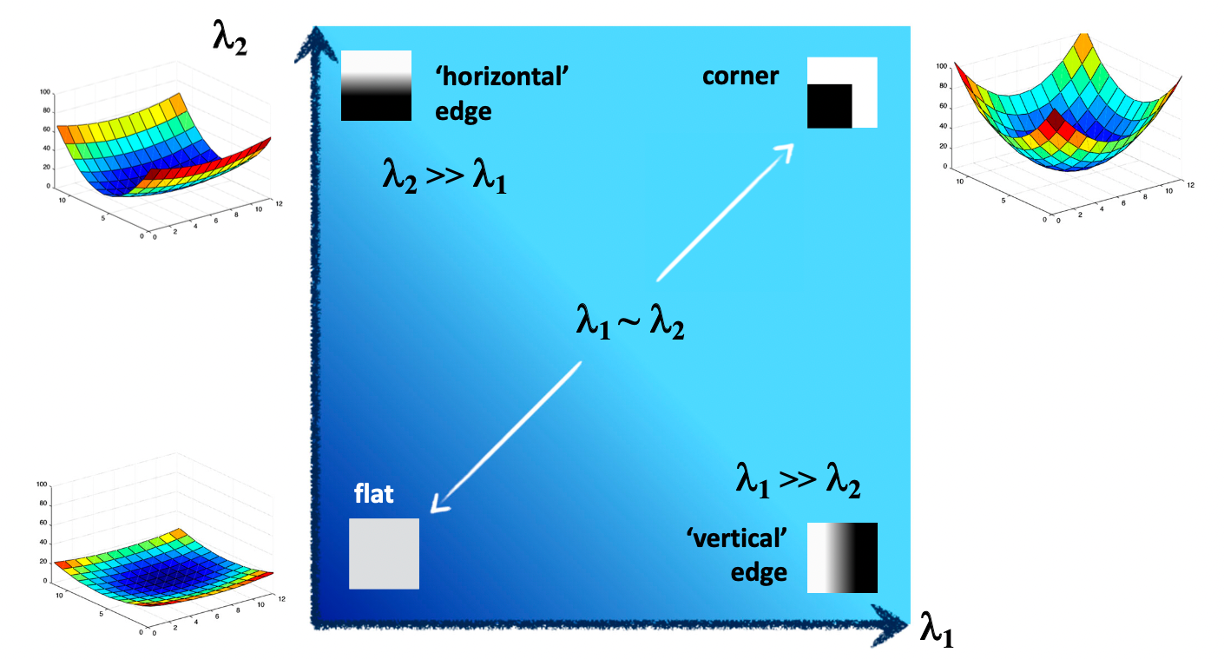
$\lambda_1$와 $\lambda_2$의 값이 비슷하면서 0에 가까울 경우 이것을 flat 한 영역의 그래프를 나타냅니다. $\lambda_1$와 $\lambda_2$ 값 중 어느 하나만 클 경우에 이는 edge 영역을 나타냅니다. 물론 어느 값이 더 큰 지에 따라 이것이 horizontal 인지, vertical 인지는 eigenvector 가 기준이 되겠죠? 마지막으로, $\lambda_1$와 $\lambda_2$의 값이 비슷하면서 둘 다 클 경우, 이것은 corenr 를 의미하는 것이죠.

5. Use threshold on eigenvalues to detect corners

그럼 $\lambda_1$와 $\lambda_2$ 가 어떤 값보다 클 때 우리는 corner 라고 해야할까요? thresholding 해야겠죠? 그런데 thresholding 을 해야 하는 값이 $\lambda_1$, $\lambda_2$ 로 두 개이기 때문에 우리는 이 두 값을 모두 적용한 하나의 기준 이 되어줄 응답 함수 $R$ 이 필요합니다. 가장 간단하게 생각할 수 있는 것은 $R=min(\lambda_1,\lambda_2)$ 입니다. 두 값 중 더 작은 값을 기준으로 thresholding을 하게 되면 아래와 같이 대각선 위 직사각형 영역이 corner 가 될 것입니다.

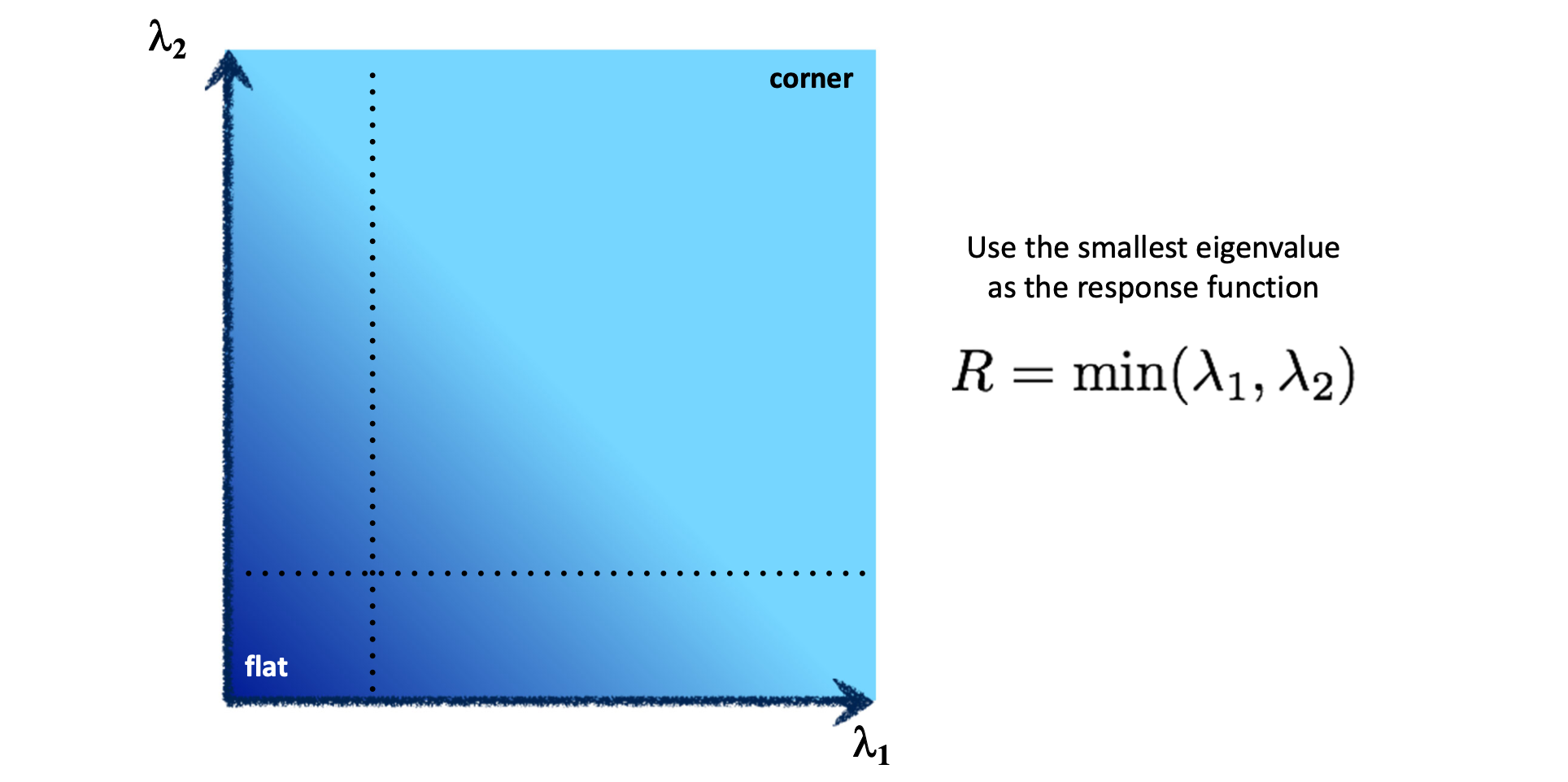
실제로 Harris Corner Detection 에서 사용하는 $R$은 아래와 같습니다.

$R = \lambda_1\lambda_2 -k(\lambda_1 + \lambda_2)^2$

이 $R$ 을 토대로 thresholding을 하게 되면 corner 의 영역은 아래와 같은 형태가 됩니다.

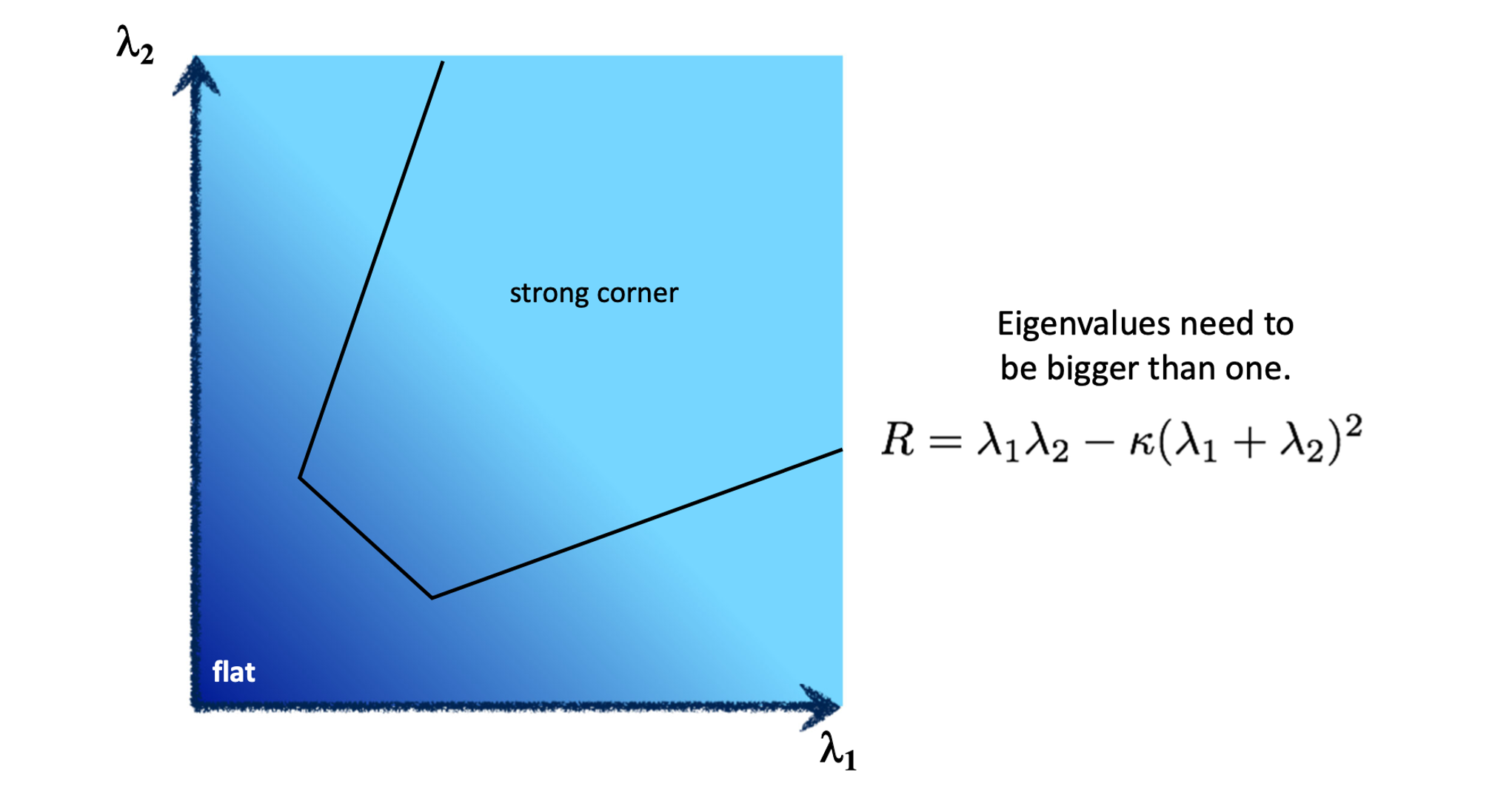
이 식에서 쓰이는 항인 $\lambda_1\lambda_2$ 와 $\lambda_1 + \lambda_2$ 는 아래 그림과 같이 matrix $M$에서 determinant 와 trace 를 활용하여 구할 수 있습니다. 이를 통해 최종적으로 우리는 $R=det(M)-ktrace^2(M)$ 으로 컴퓨터 상에서 계산할 수 있게 되는 겁니다.

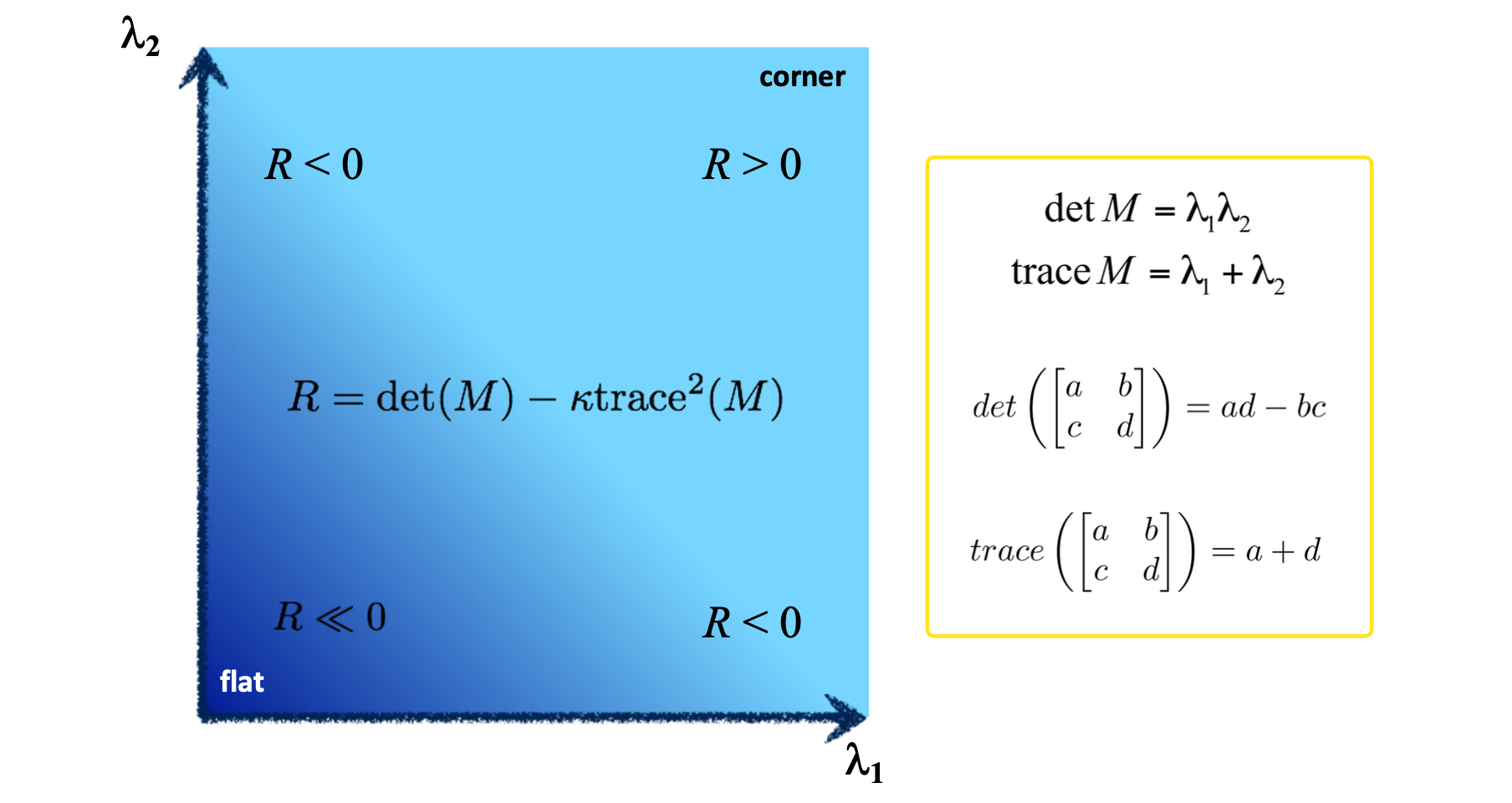
이 $R$ 을 이용하면 0 보다 클 때 corner 라고 판단할 수 있다고 합니다. 0 보다 작을 때는 edge 이면 0보다 많이 작은 threshold 보다도 작을 경우에 flat 영역이라 판단할 수 있게됩니다. (부록으로, Nobel은 $R=\frac{det(M)}{trace(M) + \epsilon}$ 으로 정의하기도 했습니다.)

Conclusion

다시 정리하자면, Harris Corner Detector 의 과정을 다음과 같이 나열할 수 있습니다.

0. Convert a color image into a grayscale image.
1. Compute partial derivatives at each pixel.
2. Compute second moment matrix $M$
   in a Gaussian window around each pixel.
3. Compute corner response function R
4. Threshold $R$
5. Find local maxima of response function (Nonmaximal suppression)**

2 에서 확인할 수 있듯이 Harris Corner Detector 는 window function $w(x,y)$ 로 Gaussian 을 사용합니다. 마지막 5의 Nonmaximal Suppression 은 과정은 중복적으로 나온 주위의 corner 중 하나만 남기기 위한 작업입니다. 픽셀 단위로 이루어지는 detection 이기 때문에 실제로 하나의 corner 인데도 굉장히 많이 검출되어 이와 같은 과정이 필요한 것이죠.

이 과정을 실제로 적용해본 결과는 아래와 같습니다.

결과에서 생각보다 많은 corner 가 검출되는 것을 보니 threshold 를 작게 설정하였나 보네요😁

부가적으로 확인할 몇 가지에 대해서만 설명드리고 마치도록 하겠습니다.

Corner Detection을 하는 과정에서 우리는 Intensity 를 미분하는 Derivative 를 수행합니다. $I_x = \frac{dI}{dx}$ 이며, $I_y = \frac{dI}{dy}$ 로 하였죠? 여기서 모든 픽셀값이 $a$ 만큼 더 해진다면, 즉 $I \rightarrow I + a$ 라면 우리가 알다시피 미분 값에는 변화가 없습니다. 그러나 $a$ 가 곱해진다면, 즉 $I\rightarrow aI$ 라면 미분 값 또한 $a$ 배 증가합니다.

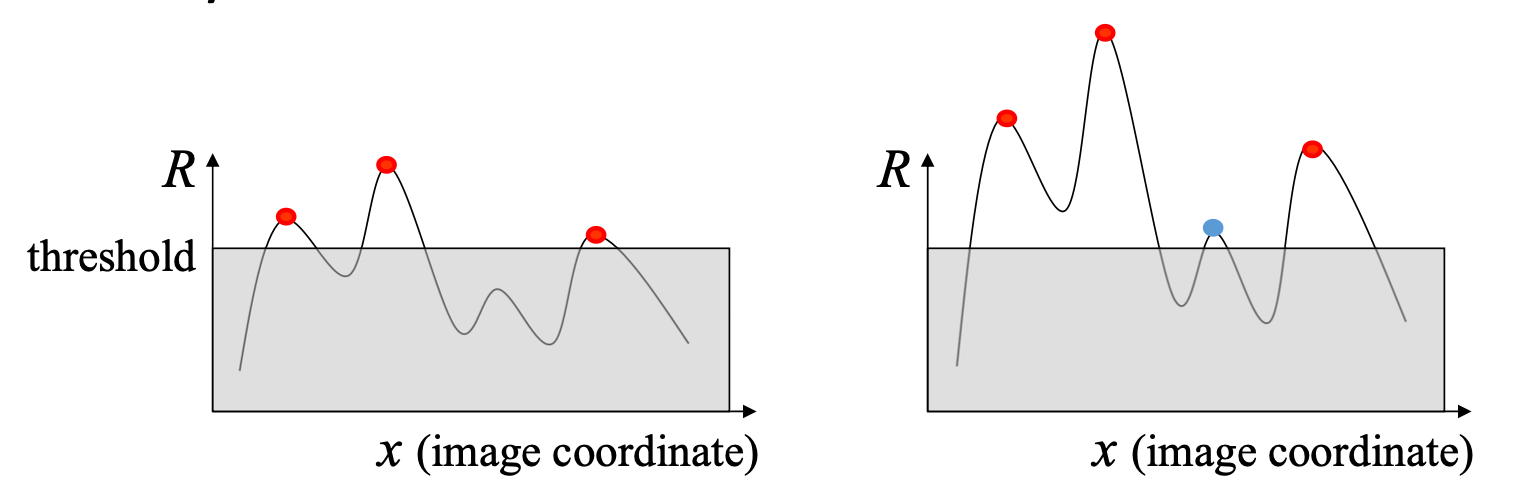
그렇게 되면 위와 같이 원래는 threshold 에 걸리지 않던 값이 threshold 에 걸리게 되는 경우가 발생할 수 있습니다. 이를 유념하셔야 된다는 말을 드리고 싶었습니다.

두 번째는 이미 아시다시피 이번 Detection 에서는 코너의 각도 를 고려하지 않는다는 것입니다. eigenvalue 만 고려 하였으니까요. 만약 고려하고 싶다면 eigenvector 를 반영해야 할 것입니다.

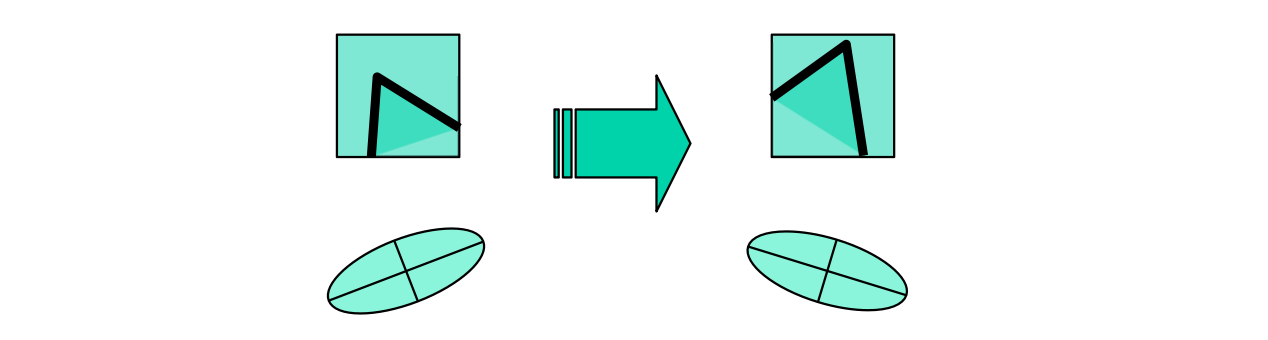
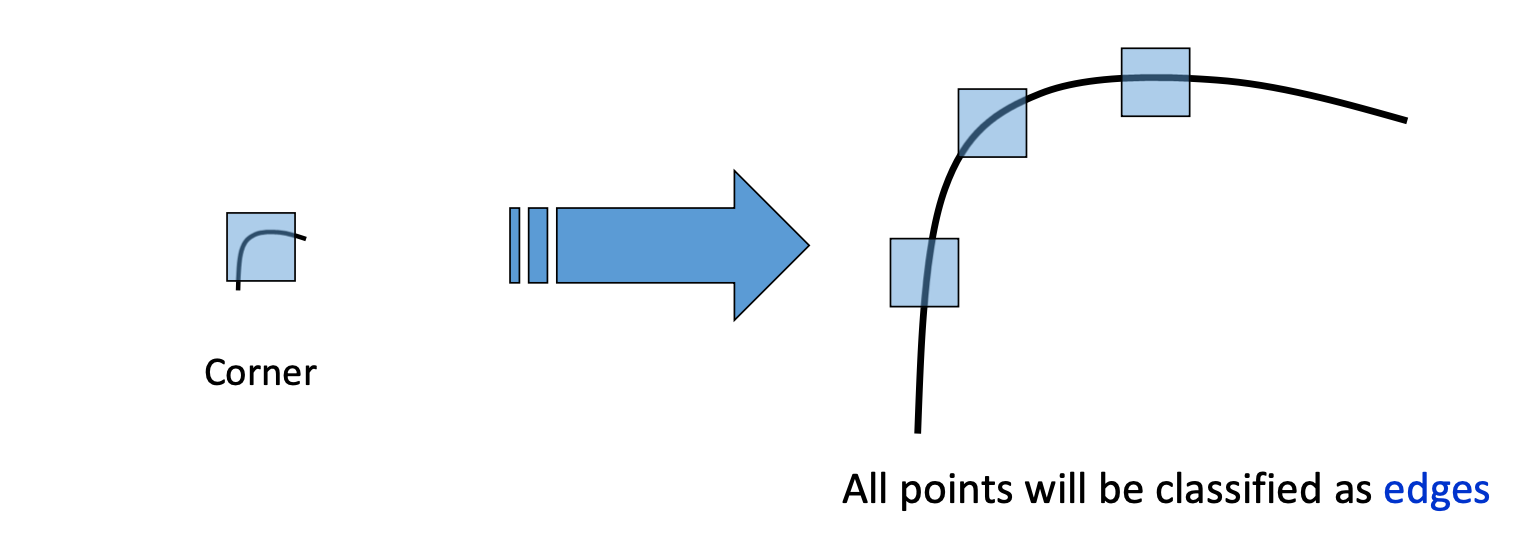
마지막으로 세 번째는 Image Scaling 입니다. 즉, 이미지의 크기 자체를 키우게 되면 왼쪽과 같이 corner 였던 영역이 같은 윈도우를 사용하면 edge로 분류되는 현상이 발생할 수 있습니다. Harris Corner Detection이 Image Scaling 에 민감하지 않아서입니다...😅