2024년 5월 3일 세미나 내용

Goal

Revisit the use of gradient information in GradCAM and discuss our concerns of why gradients may not be an optimal solution to generalize CAM
Introduce gradient-free visual explanation method (Score-CAM), which bridges the gap between perturbation-based and CAM-based methods

Motivation

CAM creates localized visual explanations but is architecture sensitive, a global pooling layer is required to follow the convolutional layer of interest

Contribution

Increasing in Confidence in the designing of weight for activation map
Gets rid of the dependence on gradients and has a more reasonable weight representation

Background

Limits of CAM and Grad-CAM
The biggest restriction of CAM is that not every model is designed with a global pooling layer
More Fully Connected Layer exists in the function(VGG model)

CAM
Takes the output from the last convolutional layer l − 1 and feeds the pooled activation to a fully connected layer l+1 for classification

wcl,l+1[k] is the weight for k-th neuron after global pooling at layer l
There is no global pooling layer or there is no (or more than one) fully connected layer(s), CAM will fail due to no definition of αc

Grad-CAM

Using the gradient to incorporate the importance of each channel towards the class confidence is a natural choice and it also guarantees that Grad-CAM reduces to CAM if there is only one fully connected layer following the chosen layer

Gradient-Issue

The weights for activation maps (2)-(4) are 0.035, 0.027, 0.021
(2) has the highest weight but cause less increase on target score

Saturation

Vanish due to the saturation problem for Sigmoid function or the zero-gradient region of ReLU function

False Confidence

Ail and Ajl , if the corresponding weight αc i ≥ αc j , the input region which generates Ai l is at least as important as another region that generates Aj l towards target class ‘c’
Activation maps with higher weights show lower contribution to the
network’s output compared to a zero baseline
This phenomenon may
be caused by the global pooling operation on the top of the
gradients and the gradient vanishing issue in the network

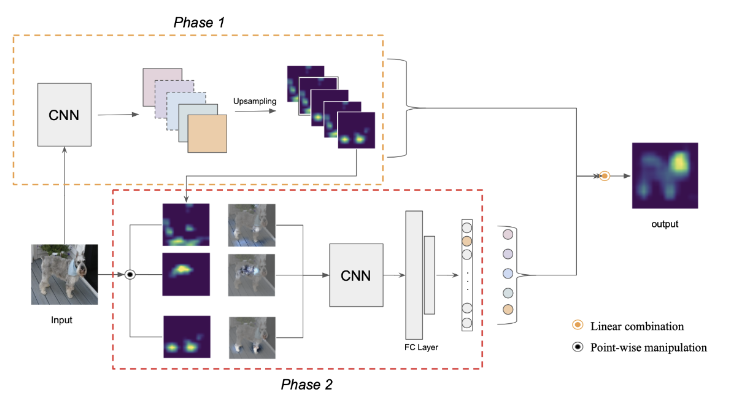
Score-CAM: Proposed Approach

In contrast to previous methods, Score-CAM incorporate the importance as the Increase of Confidence

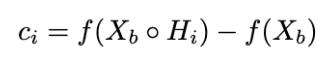
Y = f (X) that takes an input vector X =[x0, x1, ..., xn]> and outputs a scalar Y . For a known baseline input Xb, the contribution ci of xi, (i ∈ [0, n − 1]) to wards Y is the change of the output by replacing the i-th entry in Xb with xi

Generate Def.3 to Channel-wise Increase of Confidence in order to measure the importance of each activation map

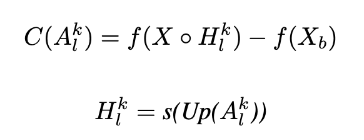
An internal convolutional layer l in f and the corresponding activation as A. Denote the k-th channel of Al by Ak l

Up(·) denotes the operation that upsamples Ak l into the input size 4 and s(·) is a normalization function that maps each element in the input matrix into [0, 1]

Consider a convolutional layer l in a model f , given a class of interest c

C(·) denotes the CIC score for activation map Ak l

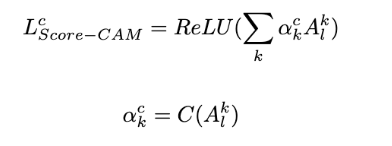
Experiments

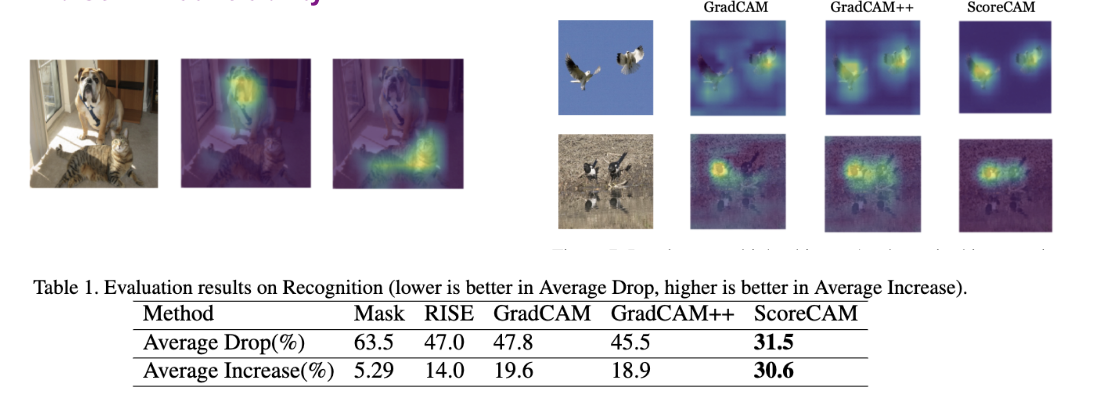
The VGG-16 model classifies the input as ‘bull mastiff’ with 49.6% confidence and ‘tiger cat’ with 0.2% confidence, Score-CAM correctly gives the explanation locations for both of two categories

Score-CAM to distinguish different categories, because the weight of each activation map is correlated with the response on target class, and this equips Score-CAM with good class discriminative ability