[paper-review] Ultradense Word Embeddings by Orthogonal Transformation

Rothe, Sascha, Sebastian Ebert, and Hinrich Schütze. "Ultradense word embeddings by orthogonal transformation." arXiv preprint arXiv:1602.07572 (2016).

---

Abstract

• Densifier

  • 수백차원 정도의 단어 임베딩 벡터(word embedding)를 단일 차원정도로 극도로 축소하는 방법
  • 직교 변환(orthogonal transformation)을 변환을 위한 행렬(matrix)를 학습.

• 장점

  • 단어의 감정(sentiment), 구체성(concreteness), 빈도(frequency) 정보를 초고밀도(ultradense) 공간에 표현할 수 있음.
  • 이 압축된 임베딩 벡터를 사용하는 모델들은 효율적이고 컴팩트하게 학습할 수 있음.

---

1. Introduction

결국 모든 task에 유용한 일반적인(generic) 특징 표현(representations)은 초고밀도 벡터 공간에서 찾을 수 있을 것이라는 가설을 기반한다.

Densifier는 기존 임베딩 공간(original space), $E_o$를 orthogonal transformation을 거쳐 초고밀도 벡터 공간(ultradense subspace), $E_u$로 만들어 내는 방법을 학습한다.

---

2. Method

• $Q \in \mathbb{R}^{d \times d}$(orthogonal matrix): 기존 단어 임베딩 공간(original space)을 특정 정보만 지닌 작은 차원으로 변환하는 행렬

  • 감정 정보(sentiment information)을 담은 벡터를 만드려는 $Q$를 거치면
  • $D^s$의 초고밀도 공간으로 변환된다.
    $\begin{cases} D^s \subset \{1, ..., d\} & with \space \mathrm{sentiment \space information}\\ \{1, ..., d\}\backslash D^s & without \space \mathrm{sentiment \space information} \end{cases}$
  • 같은 방식으로 구체성(concreteness), 빈도(frequency) 정보는 각각 $D^c, D^f$의 공간에 압축될 것이다.
  • 단, 각각 $D^s, D^c, D^f$는 서로 겹치지 않는다고 가정한다.

• $e_w \in E_o \subset \mathbb{R}^d$: 단어 $w$의 기존 임베딩(original embedding)

• $d^s$: 공간 $D^s$의 차원 수

  • 편의를 위해 각각 sentiment, concreteness, frequency를 의미하는 첨자 $s, c, f$는 $*$로 통일하여 표기
  • $D^*$: $D^s, D^c, D^f$를 모두 포함
  • $d^*$: $d^s, d^c, d^f$를 모두 포함

• $P^* \in \mathbb{R}^{d^* \times d}$: 기존 $d$차원에서 초고밀도 공간 $d^*$차원으로 축소하는데 사용되는 항등행렬(identity matrix)

단어 $w$의 초고밀도 임베딩 표현 $u^*_w \in E_u \subset \mathbb{R}^{d^*}$는 아래와 같이 정의.

2.1. Separating Words of Different Groups

어휘 정보(lexicon resource) $l$을 아래와 같이 정의.

• $L^*_{\nsim}$: $l^*(v) \ne l^*(w)$를 만족하는 단어 쌍 $(v, w)$ 집합일 때. 즉, 다른 레이블이 지정된 단어들.
• 두 단어의 임베딩 간 거리를 최대화하는 목적함수는 아래 값을 최대화한다.
• $\sum_{(v, w) \in L^*_{\nsim}} \lVert u^*_v-u^*_w \rVert,$
  즉, 다시말하면,
  $\argmax_Q \sum_{(v, w)\in L^*_{\nsim}} \lVert P^*Q(e_w - e_v) \rVert\\ =\argmin_Q \sum_{(v, w)\in L^*_{\nsim}} -\lVert P^*Q(e_w - e_v) \rVert$
• 서로 다른 레이블인 단어를 점점 멀리 위치하도록 학습한다.

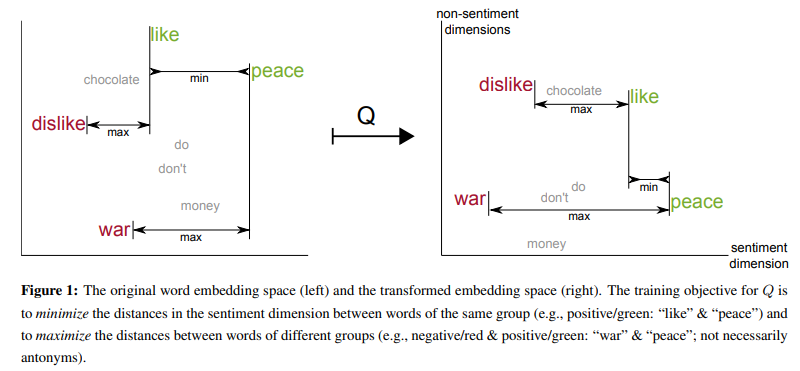
2.2. Aligning Words of the Same Group

같은 방식으로,

• $L^*_{\sim}$: $l^*(v) = l^*(w)$를 만족하는 단어 쌍 $(v, w)$ 집합일 때. 즉, 같은 레이블이 지정된 단어들.
• 두 단어의 임베딩 간 거리를 최소화하는 목적함수
• $\argmin_Q \sum_{(v, w)\in L^*_{\nsim}} \lVert P^*Q(e_w - e_v) \rVert$
• 서로 같은 레이블인 단어를 점점 가깝게 위치하도록 학습한다.

2.3. Training

2.1과 2.2의 목적함수를 결합.
두 목적함수의 기여도 조정, 가중하기 위한 hyper-parameter $\alpha^*$, $1-\alpha^*$를 사용한다.

• Stocastic gradient descent (SGD)
• Batch size=100
• learning rate=5에서 시작해 학습이 진행될 때마다, 0.99를 곱해 점점 낮춘다.

2.4. Orthogonalization

$Q$를 학습할 때마다 업데이트되는 $Q'$은 직교 행렬이 될 수 없다.
따라서 다시 $Q'$을 직교화(orthogonalize).

Singular value decomposition(SVD)을 통해 $Q'$과 가장 가까운, 비슷한 직교 행렬을 찾는다.

로 SVD되었을 때, 2-norm, Frobenius-norm의 측면에서 가장 가까운 직교행렬 $Q$는 아래와 같다:

$Q$를 학습하는 시간은 논문의 모든 실험에서 5분 미만의 시간이 소요되었다.

---

3. Lexicon Creation

다섯가지 언어, 두 가지 도메인에 대한 실험 환경 세팅
Language; 영어, 독일어, 체코어, 불어, 스페인어
Domain; Twitter Corpus, 뉴스 Corpus
Lexicon Resource(Label); Sentiment, Concreteness, Frequency

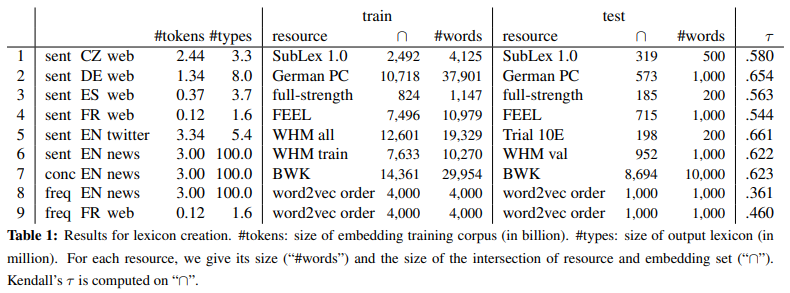
Kendall's $\tau$는 순위 상관 계수(rank correlation coefficient)의 한 종류,
두 변수들 간의 순위를 비교하여 연관성을 계산한다.
자세한 설명은 여기에서.

---

4. Evaluation

4.1. Top-Ranked Words

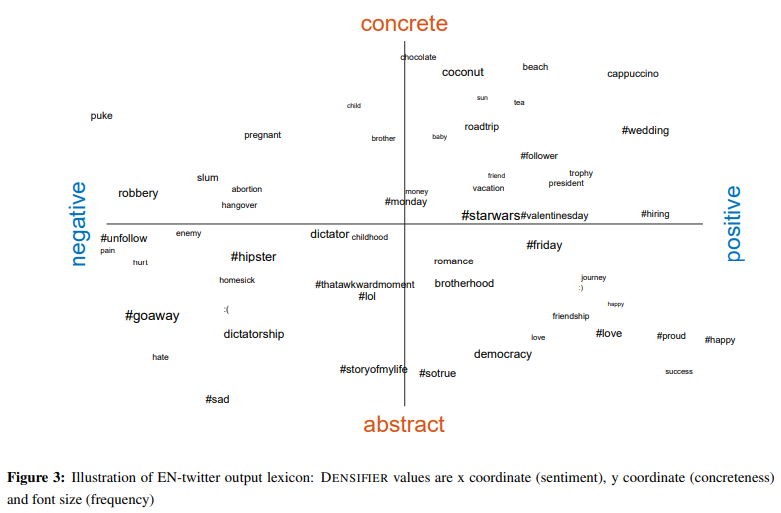
• 첫 번째 리스트 EN-twitter의 sentiment top-10 리스트를 보면 #(hashtag)를 볼 수 있다.
• 여기에서 사용한 WHM lexicon resource가 "#"를 포함한 단어는 하나도 없었는데, 트위터에 자주 사용되는 "#"를 사용한 #blessed를 top-1 positive 단어로 택한 것을 볼 수 있다.

4.2. Quality of Predictions

• Sentiment, concreteness에 대한 분석 결과는 좋았지만, frequency에 대한 결과는 좋지 않았다.
• 규모가 큰 임베딩 Corpus를 사용한 영어의 결과가 작은 규모의 Corpus를 사용한 불어의 결과보다 좋았다.

4.4. Text Polarity Classification

초고밀도 임베딩이 성능 저하는 없으면서, 모델의 학습시간을 단축할 수 있는지에 대한 실험이다.

1. 400차원의 기존 단어 임베딩
2. Densifier로 축소한 40차원 임베딩
3. Densifier로 축소한 4차원 임베딩

을 linguistically-informed convolutional neural network (lingCNN)으로 학습한 결과.

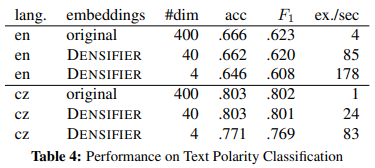
• 약간의 성능 저하만 있었으며, 계산 속도의 향상이 뚜렸하게 보였다.
• 영어에서의 결과보다 체코어에서의 결과가 좋았다.
  • 체코어의 lexicon resource가 매우 적었다는 점을 미루어볼 때, 고무적인 결과이다.

---

5. Parameter Analysis

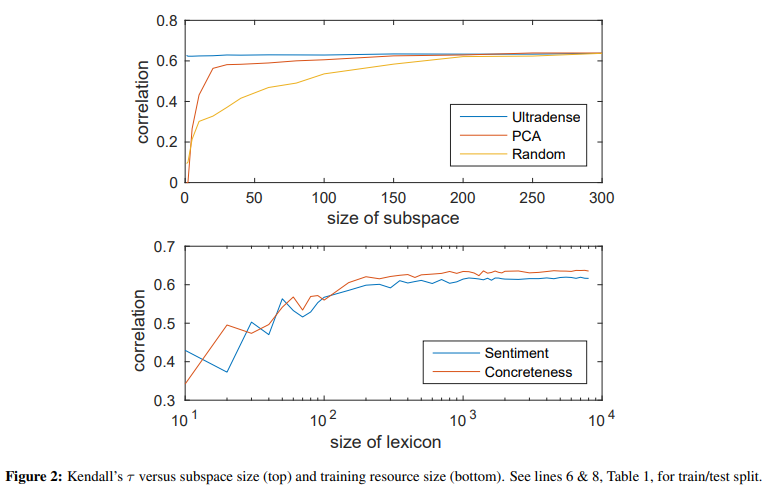
5.1. Size of Subspace

초고밀도 공간 차원 $d^*$을 어떻게 할지에 대한 답변이다.

Sentiment 분석에서 어떤 차원의 정보를 활용할지 세 가지 환경을 비교했다.

1. Random : 원래 임베딩의 $d^s$차원의 정보 사용
2. PCA : 주성분분석(PCA)를 거쳐 제 1 주성분을 사용
3. Ultradense : 초고밀도 공간으로 압축한 정보 사용

• Ultradense의 실험결과는 $d^s=1$일 때에도 일정한 성능을 보인다.

5.2. Size of Training Resource

많은 단어들은 지정된 레이블들, lexicon resource의 퀄리티가 떨어지는 경향이 있다.
좋은 변환 행렬 $Q$를 만드는 데 필요한 lexicon resource의 크기는 어떻게 될까?

• 300개 정도의 레이블이 지정되면 준수한 성능을 보인다.

---

7. Conclusion

단어 임베딩(word embeddings)을 1차원까지도 차원을 줄이는 초고밀도 임베딩 방법을 소개.

• 기존 임베딩 공간보다 100배 적은 차원으로 축소.
• 불필요한 노이즈 정보를 제거, 과 적합 방지
• 빠른 학습 속도, 더 적은 학습 파라미터

---