시작하기
나이를 기준으로, 키를 예측하는 선형 예측 회귀 모델을 생성하자.
목표: 오차함수로, MSE를 사용하고 오차를 줄이기 위해 Gradient Descent를 사용하자.
Feature Vector 생성하기
모델 구현의 편의를 위해, Feature Vector(나이)의 차원은 1D로 사용한다. 사용될 데이터는 x 는 총 16개이다.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(seed=1)
x_min = 4 # 최소
x_max = 30 # 최대
x_n = 16 # 데이터 수
x = 5 + 25 * np.random.rand(x_n) # 나이
print("Feature Vector (나이): \n",x)
print("Dimension:", x.shape)Feature Vector (나이):
[15.42555012 23.00811234 5.00285937 12.55831432 8.66889727 7.30846487
9.65650528 13.63901818 14.91918686 18.47041835 15.47986286 22.13048751
10.11130624 26.95293591 5.68468983 21.76168775]
Dimension: (16,)입력 벡터의 종속 변수(함수 값 y)인 Target Value(키)를 생성하자.
참고: np.random.rand(d0,d1..dn)은 단변량 가우시안 분포로 평균 0 분산 1인 난수를 주어진 Shape로 생성한다.
Prm_c = [170, 108, 0.2]
T = Prm_c[0] - Prm_c[1] * np.exp(-Prm_c[2] * x) + 4 * np.random.randn(x_n) # 생성 매개변수
print("Target Value(키): \n", T)
np.savez('ch5_data.npz', x=x, x_min=x_min, x_max=x_max, x_n = x_n, t=T) # 나이 / 키 데이터를 npz 확장자로 저장 후 불러올 예정참고: np.savez는 numpy 배열을 저장하는 확장자로 np.load를 통해 저장한 데이터를 불러올수 있다.
Target Value(키):
[170.91013145 160.67559882 129.00206616 159.70139552 155.46058905
140.56134369 153.65466385 159.42939554 164.70423898 169.64527574
160.71257522 173.28709855 159.31193249 171.51757345 138.9570433
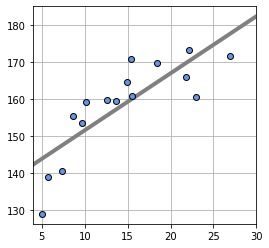
165.8744074 ]각 입력 데이터에 대응하는 출력 데이터를 그래프로 표현하면 다음과 같다.
plt.figure(figsize=(4,4))
plt.plot(x, T , marker='o', linestyle='None', markeredgecolor='black') # marker은 동그라미 마커뜻함.
plt.xlim(x_min,x_max)
plt.grid(True)
plt.show()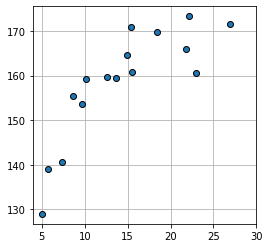
직선 모델의 데이터 예측
Lost Function과 Gradient Descent를 활용하여 직선 ()을 만들어 보자.
np.savez 메소드를 통해 저장한 ch5_data.npz파일을 볼러와서 사용할 변수 x_min, x_max, x_n를 지정한다.
data_npz = np.load('ch5_data.npz')
data_npz.files['x', 'x_min', 'x_max', 'x_n', 't']x_min = int(data_npz['x_min'])
x_max = int(data_npz['x_max'])
x_n = int(data_npz['x_n'])
T = data_npz['t']MSE
모델의 성능을 평가하는 MSE 구현 하기
def mse_line(x, t, w): #[기울기, 편차]
y = w[0] * x + w[1] # 1D 방정식
mse = np.mean((y - t) ** 2) # Numpy Array로 받은 벡터 각각의 Element끼리 뺀다
return mseGradient Descent
MSE의 오차를 줄이기 위한 Gradient Descent 함수 구현하기.
- : 직선의 기울기
- : y 절편
# 경사 하강법
def dmse_line(x, t, w):
y = w[0] * x +w[1]
d_w0 = 2 * np.mean((y - t)*x)
d_w1 = 2*np.mean(y-t) # 편차
return d_w0, d_w1 # Return value by tuple array
d_w = dmse_line(x, T, [10, 165]) # 나이, 키, [기울기, 편차] >> 임의의 매개변수를 전달해서 오차를 줄여나가자 Optimizing MSE using Gradient Descent
기울기 와 절편 의 최적값을 찾기위한 (기울기 ≈ 0) fit 함수 구현. fit_line_num의 매개변수인 w_init은 가중치 초기 값으로, 학습을 통해 조정된다.
alpha: Learning Parameter로, 의 다음 기울기 를 찾기위한 Stepi_max: 최대 반복 횟수eps: End Point로, 충분한 결과가 나왔을때 종료 조건.
def fit_line_num(x,t,w_init): # 입력값과 정답을 넘겨주는걸 이제 알아야지?
# w_init = [10.0, 165.0] # 초기값
alpha = 0.001 # Learning Rate, 하이퍼 파라미터
i_max = 100000 # 종료조건 1 : 10만번만 반복
eps = 0.1 # 종료조건2: 기울기 절대 값이 충분히 작아 졌을때
w_i = np.zeros([i_max,2]) #100,000 x 2 행렬. 각 행에는 시작때부터 끝날대까지 w0, w1값을 저장
w_i[0, :] = w_init # 최초값 저장.
for i in range(1, i_max): # w_i에 저장할때, i값을 이용해서 w_i의 리스트에 게속 집어넣는거임. 종료조건 1
dmse = dmse_line(x, t, w_i[i-1] ) #
w_i[i, 0] = w_i[i-1, 0] - alpha * dmse[0]
w_i[i, 1] = w_i[i - 1, 1] - alpha * dmse[1]
if max(np.absolute(dmse)) < eps:
break
w0 = w_i[i, 0]
w1 = w_i[i, 1]
w_i_hist = w_i[: i, :] # 현재까지 업데이트된 매개변수를 행렬로 저장
return w0, w1, dmse, w_i_hist # W Init
w_i = [10.0, 165.0]
# 초기 가중치의 MSE
mse_i = mse_line(x,T, w_i)
# 경사하강법 호출
W0, W1, dMSE, W_history = fit_line_num(x, T, w_i)학습한 모델을 그래프에 plot하기
학습된 기울기 와 y절편 을 함수 show_line에 전달하여, 그래프 그리기.
def show_line(w):
plt.figure(figsize=(4,4))
xb = np.linspace(x_min, x_max, 100) # 직선을 그리기위해
y = w[0] * xb + w[1]
plt.plot(xb, y, color=(0.5, 0.5, 0.5), linewidth=4)# 결과보기
print('W Init=[{0},{1}]'.format(w_i[0],w_i[1]))
print('MSE Init={0:.3f} cm^2'.format(mse_i))
print('반복 횟수 {0}'.format(W_history.shape[0]))
print('dMSE=[{0:.6f}, {1:.6f}]'.format(dMSE[0], dMSE[1]))
W =np.array([W0,W1])
mse = mse_line(x,T, W)
print('W Opt=[{0:.6f}, {1:.6f}]'.format(W0, W1))
print("mse={0:.3f} cm^2".format(mse))
print("Standard Deviation={0:.3f} cm".format(np.sqrt(mse)))# 표준편차 >> 분산의 제곱근, 분산 = 편차 제곱의 평균, 편차 = 데이터 - 평균
show_line(W)
plt.plot(x,T,marker='o', linestyle="None", color='cornflowerblue', markeredgecolor='black')
plt.xlim(x_min,x_max)
plt.grid(True)
plt.show()최종
fit_line_num의 인자로 전달한 초기값 W Init은 [10.0, 165.0]의 손실함수 값이 Gradient Descent를 통해 25745.845 -> 49.027으로 최적화된것을 확인할 수 있다.
W Init=[10.0,165.0]
MSE Init=25745.845 cm^2
반복 횟수 13819
dMSE=[-0.005794, 0.099991]
W Opt=[1.539942, 136.176260]
mse=49.027 cm^2
Standard Deviation=7.002 cm