시작

이번에는 4번째 포스팅으로 차원축소에 대해 포스팅 해보겠다. 차원축소는 개념만 조금 알고있어 부족한데 이번 공부 기회를 통해 부족한 개념을 보완하겠다.

차원 축소

• 모델 학습에 불필요한 피처나 방해되는 피처를 제거하면서 속도,성능을 향상하는 방법
• 방해되는 피처는 over-fitting 문제를 발생시키는 피처라고 볼 수 있음

차원의 저주

• 공간의 차원이 증가함에 따라 빈공간이 많아지며 , 정보가 없는 공간이 많아지는 현상
• 차원을 축소시키면서 해결 가능

차원 축소 방법

형상 선택

• 종속 변수와 가장 관련성이 높은 피처만을 선택해, 나머지를 제외시키는 방법
• 피처 사이의 상관 관계가 매우 높아서, 한 쪽이 의미 없는 경우 제외시킴 예) 공분산 분석

형상 추출

• 개별 피처를 제거하는 대신, 저차원 공간으로 투영시켜 데이터와 모델을 단순화
• 예) PCA , SVD , LDA , t-SNE , UMAP

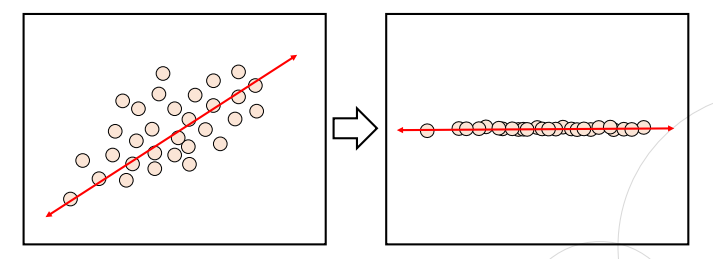
주성분 분석(PCA)

• 전체 데이터의 분포를 가장 잘 설명할 수 있는 주성분(데이터를 가장 잘 설명하는 성분)을 찾아주는 방법론
• 데이터의 분산을 최대한 보존하는 방향으로 주성분을 선택하며, 이를 통해 데이터의 중요한 특징을 유지하면서 차원을 줄임
  

특이값 분해(SVD)

• 특이값 분해는 데이터 압축을 시킬 수 있는 방법론
• SVD는 행렬을 세 개의 행렬의 곱으로 분해하는 기법

Linear Discriminant Analysis (LDA)

• 데이터를 클래스 간의 분리를 최대화하는 방향으로 변환
• 주로 패턴 인식 및 분류 문제에서 사용
• 유사성이 높은 데이터 동일한 그룹으로 분류

UMAP

• 데이터 시각화와 차원 축소를 위한 비선형 기법
• t-SNE과 비슷하지만 확장성,일관성 등에서 더 좋음

클러스터링

군집화

• 비지도 학습 상황에서, 데이터 샘플들을 별개의 군집으로 그룹화 하는 것(분류)
• 데이터 특징에 따른 세분화 , 이상검출에 사용

종류 (모수적 추정 vs 비모수정 추정)

모수적 추정

• 주어진 데이터가 특정 데이터 분포를 따른다고 가정
• GMM이 대표적

GMM (gaussian mixture model)

• 현재 추정된 모수를 통해 샘플을 군집에 할당하는 단계인 Expectation단계
• 로그 가능도(likelihood)의 기댓값을 최대화하는 모수를 추정하는 단계인 Maximization 단계
• 장점 : 각 유형별 데이터의 밀도가 일정하지 않거나, 경계가 모호해도 군집화가 잘됨
• 단점 : 클러스터 개수 k에 대한 설정 필요 , 연산량큼

비모수적 추정

• 데이터가 특정 분포를 따르지 않는다는 가정
• K-means, Mean Shift, DBSCAN 등의 알고리즘등

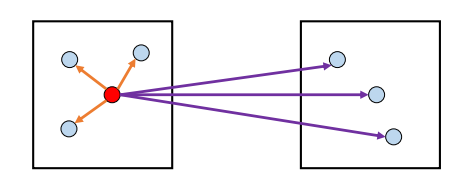
K-means

• 샘플은 가장 가까운 중심점을 가진 군집으로 할당됨
• K-means 알고리즘은 사전에 군집의 수에 대한 하이퍼파라미터 k를 정해야 사용 가능
• EM 알고리즘을 통해 최적의 군집에 수렴할 때까지 학습함

EM 알고리즘

• Expectation 단계와 Maximization 단계로 나뉨
• 샘플을 군집으로 할당 단계 / 군집에 할당된
  샘플을 바탕으로 새로운 중심점을 계산 단계

k-means 평가

실루엣 분석

• 군집들이 얼마나 효율적으로 분리되어 있는지를 보여줌
• 전체 실루엣 계수의 평균값이 클수록, 개별 군집의 평균값의 편차가 작을수록 좋음
• 실루엣 계수는 -1 ~ 1 사이의 값을 가지며, 1에 가까울수록 더 좋은 군집
  

K-means 한계점

• 군집의 개수, centroid에 대한 초기 설정값에 따라 성능 편차가 심함
• 군집 크기나 밀도가 다를 경우, 학습이 잘 안될 수가 있음
• 데이터 분포가 특이할 경우에도 군집 학습이 어려움

DBSCAN

• 밀도가 높은 부분을 중심으로 군집화를 하는 방법론
• 모든 데이터 샘플에 대해 진행하여 cluster point와 noise point를 구분
• 장점 : 다양한 형태의 군집 유형을 구분 가능 , 아웃라이어를 찾아낼 수 있음
• 단점 : 연산량이큼 , 군집의 개수 설정만 자유로움

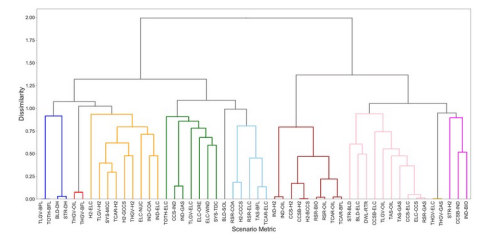
Hierarchical Clustering(계층적 군집화)

• 군집-군집 간 거리 계산을 통해 합치거나 나눔
• 데이터 세분화에 보다 적합한 방법론
• 사전에 클러스터의 수를 정하지 않아도 학습이 가능
• 덴드로그램(dendrogram)으로 개체들이 결합되는 순서를 시각화
  

후기

이번 포스팅은 차원축소 , 클러스터링 위주로 다뤄보았다. 내용이 워낙 방대하다 보니 간단하게 개념 위주로 정리했으며 , 이것으로 메타코드에 있는 머신러닝 이론강의는 마무리 되었다. SQL에 이어서 머신러닝까지 메타코드에서 수강하면서 전반적인 지식들을 정리할 수 있어서 너무 알찼다.

앞으로 데이터를 다루는 직무에 취업하기 위해 빠질 수 없는 인공지능 역량을 꾸준히 키우키위해 머신러닝 코드들도 끊임없이 접할것이며 , 좋은 강의를 제공해준 메타코드에게 감사하다.

메타코드 공식 사이트 : https://mcode.co.kr/
강의 유튜브 링크 : https://youtu.be/oyzIT1g1Z3U?feature=shared