3D Gaussian Splatting

김민솔·2024년 8월 19일

Gaussian-Splatting

목록 보기

1/6

novel-view synthesis 분야에서 많은 주목을 받고 있는 모델인 3D Gaussian splatting에 대해서 다뤄보겠습니다. 3D Gaussian Splatting은 NeRF 모델들과 달리 MLP를 사용하지 않고, 3D scene을 3차원의 가우시안들로 표현하는 모델입니다.

spec

3D GS의 이미지 퀄리티는 이전 SOTA인 Mip-NeRF360보다 뛰어난데도 불구하고, Mip-NeRF360의 Traning 속도가 약 48시간인 반면 3D GS의 Traning 속도는 약 38분 밖에 되지 않습니다(!). 뿐만 아니라 렌더링 속도(fps)도 언급된 NeRF 모델들보다 확연히 빠른 것을 확인할 수 있습니다. (real-time이라고 부르는 30 fps 이상인 것을 확인할 수 있습니다.)

1. Introduction

3D GS의 solution은 크게 3가지의 구성 요소로 이루어져 있습니다. 1️⃣ : 3D Gaussian, 2️⃣: Optimization, 3️⃣: Real-time rendering solution입니다.

1. 3D Gaussian

3D Gaussian을 선택한 이유는 다음과 같습니다.

미분 가능한 volumetric 표현 가능.
Rasterization(object를 픽셀로 매핑)이 효율적으로 이뤄짐.
- 2D projection과 $\alpha$ -blending으로 rasterization 구현됨
- NeRF에서와 동일한 Image formation model 사용

2. Optimization

3D 가우시안들의 최적화는 가우시안의 특성들을 최적화하는 것으로 구현되었습니다.

3D position: $xyz$
opacity: $\alpha$
anisotropic covariance: ( $S$ , $R$ )
spherical harmonic (SH) coefficients

해당 특성들은 adaptive density control step에서 update됩니다.

3. Real-time rendering solution

tile-based rasterization(with fast GPU sorting algorithm)을 활용하여 빠르고 정확한 rendering이 가능하게 하였습니다. 해당 알고리즘에 대해선 아래 챕터에서 다루었습니다.

2.1 Traditional Scene Reconstruction

Structure-from-Motion(SFM)을 통해서 sparse point cloud를 얻어내어 novel-view synthesis에 사용합니다. (SFM에 대한 정리 포스트입니다.[Structure-from-Motion (COLMAP) (velog.io)])

SFM으로 얻은 포인트들을 multi-view stereo(MVS)로 3D reconstruction하는 것이 Neural rendering 이전에 활용되던 방법입니다.

2.2 Neural Rendering and Radiance Fields

NeRF는 확률적 sampling과 인코딩 기법을 통해 MLP로 volumetric representation을 하였습니다. Mip-NeRF360은 이미지 퀄리티적인 측면에서, Instant NGP는 인코딩 기법을 발전시켜 Training 속도 측면에서 좋은 성능을 보였습니다. (언급한 두 개의 NeRF는 trade-off의 관계를 지닙니다.)

2.3 Point-Based Rendering and Radiance Fields

Point-based rendering과 NeRF는 같은 image formation model을 가집니다. image formation model 방정식입니다. (렌더링 파트의 color값을 구하는 식입니다.)

C = \sum_{i \in \mathcal{N}} c_i\alpha_i\prod^{i-1}_{j=1}(1-\alpha_j)

$c_i$ : color of each point
$\alpha_i = (1 - \exp(-\sigma_i\delta_i))$ : 투명도(ray를 따라 빛이 작용하는 정도), covariance $\Sigma$ 를 통해 2D 가우시안을 평가하는 데에 사용됩니다.
$T_i = \prod^{i-1}_{j=1}(1-\alpha_j)$ : ray를 따라 빛이 막히는 정도를 표현합니다.

하지만 렌더링 알고리즘에서 다른 점을 가집니다. NeRF는 continuous representation을 가지지만 sampling에서 높은 cost를 가집니다. point-based는 discontinuous representation을 가지지만 opacity와 position을 최적화하여 flexible한 특성을 지니도록 하였습니다.

3. Overiview

overview

3D GS의 알고리즘 도식도입니다. 1️⃣ (Initialization) SFM, 즉 COLMAP을 사용하여 object의 point cloud를 얻어냅니다. 이후 3D Gaussian 집합을 생성합니다. 2️⃣ 최적화 과정을 통해 radiance field representation을 생성합니다. 3️⃣ Tile-based rasterization을 통해 이미지를 빠르게 렌더링합니다. 4️⃣ backprop을 통해서 3D Gaussian들을 update합니다. 이때 Adaptive density control이 사용됩니다.

4. Differntiable 3D Gaussian Splatting

3D 가우시안의 특성들을 살펴보는 챕터입니다. 3D 가우시안의 정의부터 살펴보겠습니다.

G(x) = \exp {\{ - \frac 1 2 (x)^T\Sigma^{-1} (x) \}}

$\Sigma$ : 3D covariance matrix (in world space)
평균값은 point cloud의 point로 사용되었습니다.
이 가우시안들은 blending process에서 $\alpha$ 에 의해 곱해집니다.

3D Gaussian covariance

\Sigma = RSS^TR^T

$R$ : rotation matrix
$S$ : scaling matrix

3D Gaussian의 covariance는 ellipsoid를 구성하는 것과 유사하므로, scaling 3D vector 𝑠와 rotation을 표현하는 quaternion 𝑞로 3D covariance를 구성합니다. affine transform의 요소들로 3D covariance를 구할 수 있습니다.
위의 표현을 통해, anisotropic Gaussian을 최적화할 수 있습니다. 또한, Covariance matrix가 positive-definite 성질을 가져야 하므로, 위와 같이 정의되었습니다. (Transpose가 뒤에 나오는 형태)

3D Gaussian → 2D Projection **

3D 가우시안을 2D projection하는 과정입니다.

\Sigma' = JW\Sigma W^TJ^T

$J$ : projective transformation의 affine 근사에 대한 Jacobian 행렬
$W$ : viewing transformation

viewing transformation(world -> camera)과 Jacobian 행렬(camera -> screen)을 통해, 2D projected covariance를 구합니다.
이때, $\Sigma'$ 의 3번째 행과 열을 날려 2x2 variance 행렬을 얻을 수 있습니다.

해당 수식들이 정의되는 유도 과정은 아래 단락에서 확인하실 수 있습니다.

Semi-positive definite

covariance 행렬들이 semi-definite일 때만 물리적인 의미를 가지며, semi-positive definite를 만족하기 위하여 matrix 곱을 대칭으로 만들었습니다.

covariance == semi-definite?

https://statproofbook.github.io/P/covmat-psd.html
covariance가 semi-difinite(고유값 >= 0) 성질을 유도하는 과정입니다. Covariance를 기댓값으로 변환한 후, Y 변수로 식을 정리하여, semi-definite 성질을 증명합니다.

3D Gaussian → 2D Projection 유도 과정 + Gaussian Representation ***

Cam2World mapping

\mathcal{G}{\mathbf{v}^{''}{k}}(\psi^{-1}(\mathbf{u})-\mathbf{t}{k}) = \frac{1}{|\mathbf{W^{-1}}|}\mathcal{G}{\mathbf{v}'{k}}(\mathbf{u}-\mathbf{u}{k}) = r'_{k}(\mathbf{u})

camera 좌표계에서 world 좌표계로 좌표를 옮기는 함수는 affine mapping으로 적용됩니다.

Projection

\begin{pmatrix} x_0 \\ x_1 \\ x_2 \end{pmatrix} = \mathbf{m}(\mathbf{u}) = \begin{pmatrix}u_0/u_2 \\ u_1/u_2 \\ ||(u_0,u_1,u_2)\top||\end{pmatrix}

\begin{pmatrix} u_0 \\ u_1 \\ u_2 \end{pmatrix} = \mathbf{m}^{-1}(\mathbf{x}) = \begin{pmatrix}x_0/l\cdot x_2 \\ x_1/l\cdot x_2 \\ 1/l\cdot x_2 \end{pmatrix}

(w->c로 좌표 이동 후) camera 좌표계에 있는 3D 가우시안들을 2D로 projection하는 과정입니다. 하지만 projection matrix는 affine mapping(선형 함수가 아니므로, 적분 or 미분 불가능)이 아니라는 문제점을 가집니다. 따라서 아래와 같이 first-order Taylor Expansion을 통해 projection matrix를 근사합니다.

Taylor Expansion

\mathbf{m}_{\mathbf{u}_k}(\mathbf{u}) = \mathbf{x}_{k}+ \mathbf{J}_{\mathbf{u}_{k}}\cdot(\mathbf{u}-\mathbf{u}_k)

\mathbf{J}_{\mathbf{u}_{k}} = \frac{\partial{\mathbf{m}}}{\partial{u}}(\mathbf{u}_k)

$\mathbf{J}_{\mathbf{u}_{k}}$ : Jacobian matrix of ${\mathbf{u}_{k}}$

Taylor Expansion의 표현은 다음과 같습니다. Talyor Expansion은 특정 함수를 선형적으로 근사하는 방법입니다. (고등학교 미적분 때 배운 테일러 급수와 동일) 1계 테일러를 사용하였으며, Jacobian으로 식이 표현되었습니다.

Projected 2D Gaussian

\frac{1}{|\mathbf{W^{-1}}||\mathbf{J^{-1}}|}\mathcal{G}_{\mathbf{v}^{}_{k}}(\mathbf{x}-\mathbf{x}_{k})

$\mathcal{G}$ : Gaussian
3D Gaussian 표현 식

\begin{aligned}\mathbf{V}_{k} &= \mathbf{J}\mathbf{V}'_k\mathbf{J}^\top\\&=\mathbf{J}\mathbf{W}\mathbf{V}''_k\mathbf{W}^\top\mathbf{J}^\top\end{aligned}

$\mathbf{V}$ : 3D Gaussian covariance
$\mathbf{W}$ : world2camera transformation
$\mathbf{J}$ : Jacobian matrix

Taylor Expansion을 활용하여 가우시안을 표현하면 다음과 같습니다.

Intergration along rays → Representation

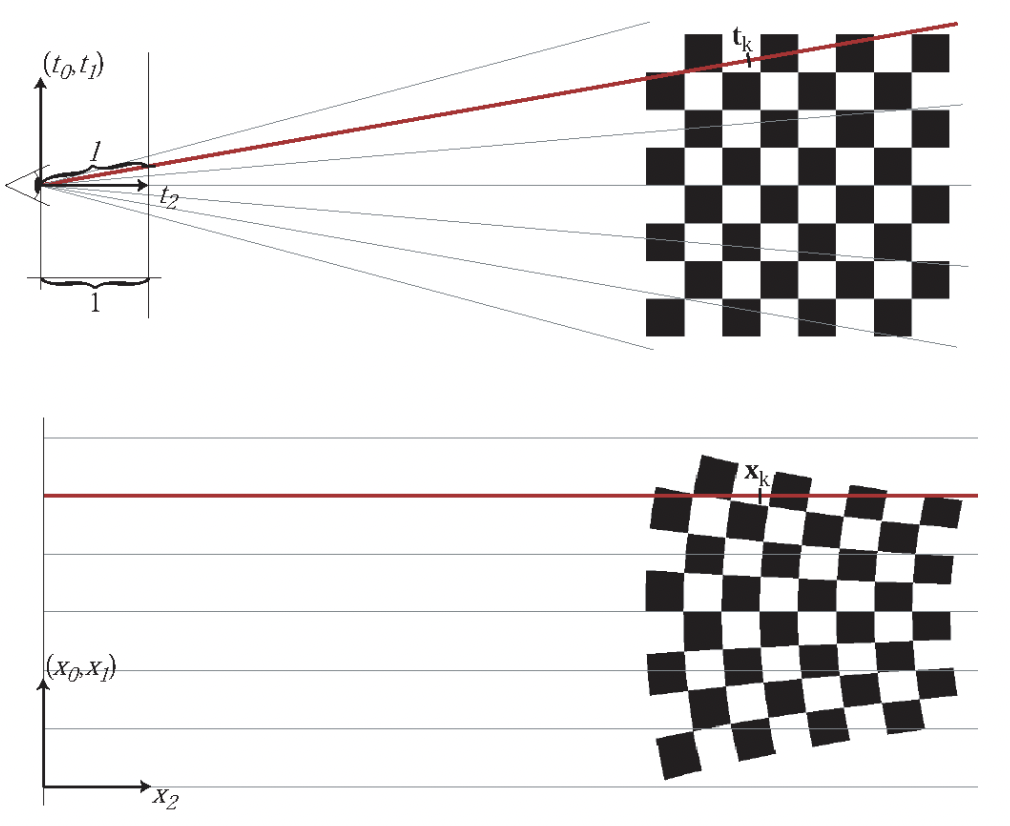
\begin{aligned}q_{k}(\hat{\mathbf{x}}) &= \int_\mathbb{R}\frac{1}{|\mathbf{W^{-1}}||\mathbf{J^{-1}}|}\mathcal{G}_{\mathbf{v}_{k}}(\hat{\mathbf{x}}-\hat{\mathbf{x}}_{k},x_2-x_{k2})dx_{2}\\&= \frac{1}{|\mathbf{W^{-1}}||\mathbf{J^{-1}}|}\mathcal{G}_{\mathbf{v}'_{k}}(\hat{\mathbf{x}}-\hat{\mathbf{x}}_{k})\end{aligned}

Ray를 따라 가우시안들을 적분하여 해당 Ray에서의 scene을 표현합니다. 이러한 과정을 거치게 되면, 위에서 언급한 것처럼 NeRF에서와 똑같은 image formation model의 식으로 scene을 표현할 수 있게 됩니다.

Code

def render: # official code에서 일부분 추출	
			// Resampling from conic of Gaussians
  		float2 xy = collected_xy[j];
			float2 d = { xy.x - pixf.x, xy.y - pixf.y };
			float4 con_o = collected_conic_opacity[j];
			float power = -0.5f * (con_o.x * d.x * d.x + con_o.z * d.y * d.y) - con_o.y * d.x * d.y;
			if (power > 0.0f)
				continue;

			// Obtain alpha by multiplying with Gaussian opacity
			// and its exponential falloff from mean.
			// Avoid numerical instabilities (see paper appendix). 
			float alpha = min(0.99f, con_o.w * exp(power));
			if (alpha < 1.0f / 255.0f)
				continue;
			float test_T = T * (1 - alpha);
			if (test_T < 0.0001f)
			{
				done = true;
				continue;
			}

			// Image formation! -> Obtain color of a pixel by Blending!!
			for (int ch = 0; ch < CHANNELS; ch++)
				C[ch] += features[collected_id[j] * CHANNELS + ch] * alpha * T;

위에서 유도한 blending 과정에 대한 forward 코드입니다. 3D Gaussian의 covariance, 2D projection covariance 등은 EWA Splatting 논문에 기재된 수식과 동일하게 코드로 구현되어 있습니다. Training 전에 가우시안 설정을 마친 후, forward + backward 과정을 거칩니다.

5. Optimization with Adaptive density control

1️⃣ positions $p$ , 2️⃣ $\alpha$ , 3️⃣ covariance $\Sigma$ , 4️⃣ SH coef들을 최적화하여 3D 가우시안들이 scene을 표현하도록 학습합니다.

학습에 사용한 기법 및 세팅들입니다.

optimization → SGD
activation function:
- sigmoid → $\alpha$ 를 [0~1) 범위로 제한 + smooth gradients 얻기 위함
- exponential → scale of the covariance
initial covariance: isotropic Gaussian (가장 가까운 세 개의 점과의 거리 = mean)
exponential decay scheduling
- Plenoxels과 유사
- positions에만 사용
Loss: $\mathcal{L} = (1-\lambda)\mathcal{L}_1 + \lambda\mathcal{L}_\text{D-SSIM}$
- $\lambda = 0.2$ (default)

Adaptive density control

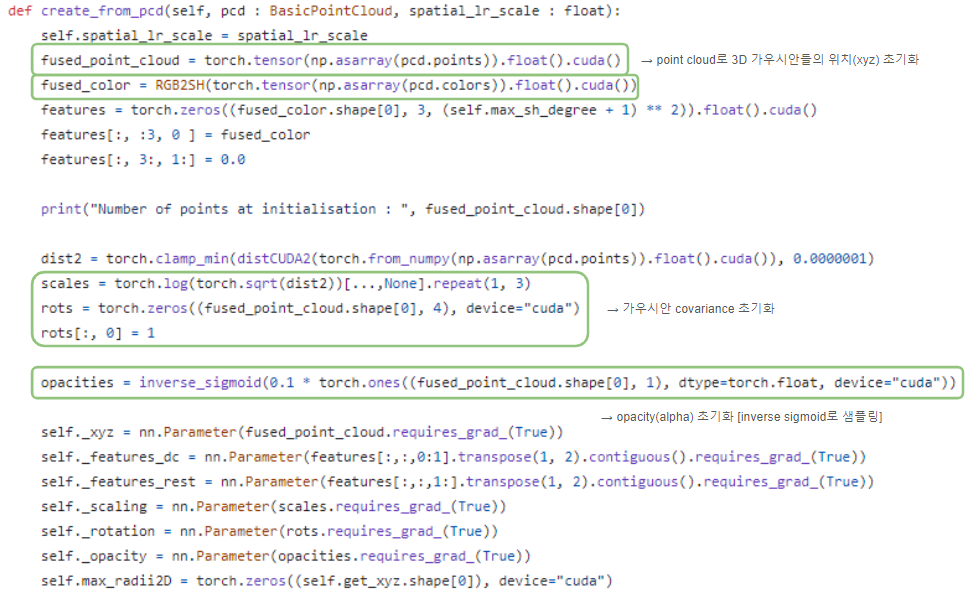
SFM으로부터 초기 가우시안 셋을 생성합니다. 이후 100 iterations에 따라 다음의 과정을 적용합니다.

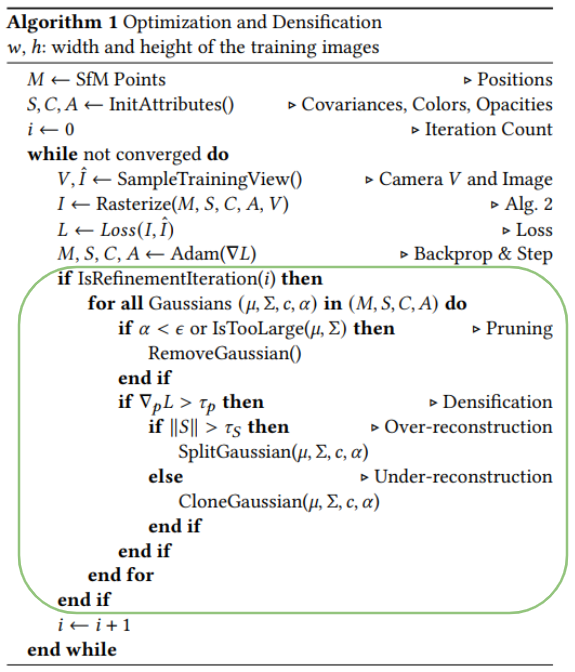
Remove

임계값 $\epsilon_\alpha$ 보다 작은 $\alpha$ 를 가지는 가우시안과 mean 혹은 covariance 값이 너무 큰 가우시안들을 제거합니다.

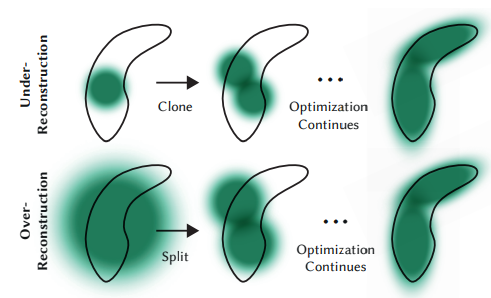
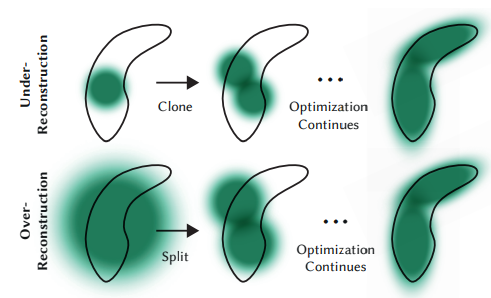
Clone

크기가 작은 가우시안들로 인해 scene이 충분하게 표현되지 못하는 경우(under-reconstructed) 작은 가우시안을 복제하여 positional gradient의 방향으로 위치시킵니다.

Split

크기가 큰 가우시안(= high variance)들이 scene에서 표현되어야 하는 영역보다 과도한 크기를 가진 경우(over-reconstructed) 해당 가우시안을 두 개로 나누게 됩니다. (by a factor of $\phi = 1.6$ ) 쪼개진 두 가우시안의 position은 쪼개기 이전 가우시안을 PDF로 샘플링하여 정해집니다.

$\alpha$ 값 조정

Optimization 과정을 거치면서, 1️⃣ 전체적인 scene의 volume과 가우시안 수를 늘리고 2️⃣ volume이 충분히 증가했다면, volume을 유지한 채로 가우시안의 수를 최대한 늘리게 됩니다.

이때 가우시안의 수가 너무 커지지 않도록 3000 iterations마다 $\alpha$ 를 0과 가까운 값으로 설정합니다. 최적화가 이루어지면서 임계값보다 낮은 $\alpha$ 의 가우시안이 제거되기 때문입니다.

정리하면서 생긴 나만의 정리

scene을 표현할 때에 가우시안의 크기가 너무 작으면 Ctrl+C + Ctrl+V, 가우시안의 크기가 너무 크면 둘로 쪼개는 알고리즘이었습니다.
outlier에 해당하는 가우시안은 Remove를 적용합니다!

6. Fast Differentiable Rasterizer for Gaussians

Rasterization을 사용하여 효율적인 $\alpha$ -blending을 구현하고자 하였습니다. rasterization 자체가 2D projection을 통해 미분 가능하며, backprop도 적은 메모리 사용으로 가능하다고 밝혔습니다.

(3D 가우시안을 2D로 projection하는 유도 과정은 위의 설명을 참고해주시면 감사하겠습니다!)

(1) CullGaussian, CreateTiles

첫 번째로는 screen을 16x16 크기의 tile들로 분할한 후에, 3D 가우시안들을 view frustum에 따라 culling하는 과정을 거치게 됩니다. 이때 view frustum이 99%의 confidence를 가지는 가우시안들만 rasterization에 이용합니다. 예시로, 아래 그림에선 연두색 가우시안이 제거됩니다.

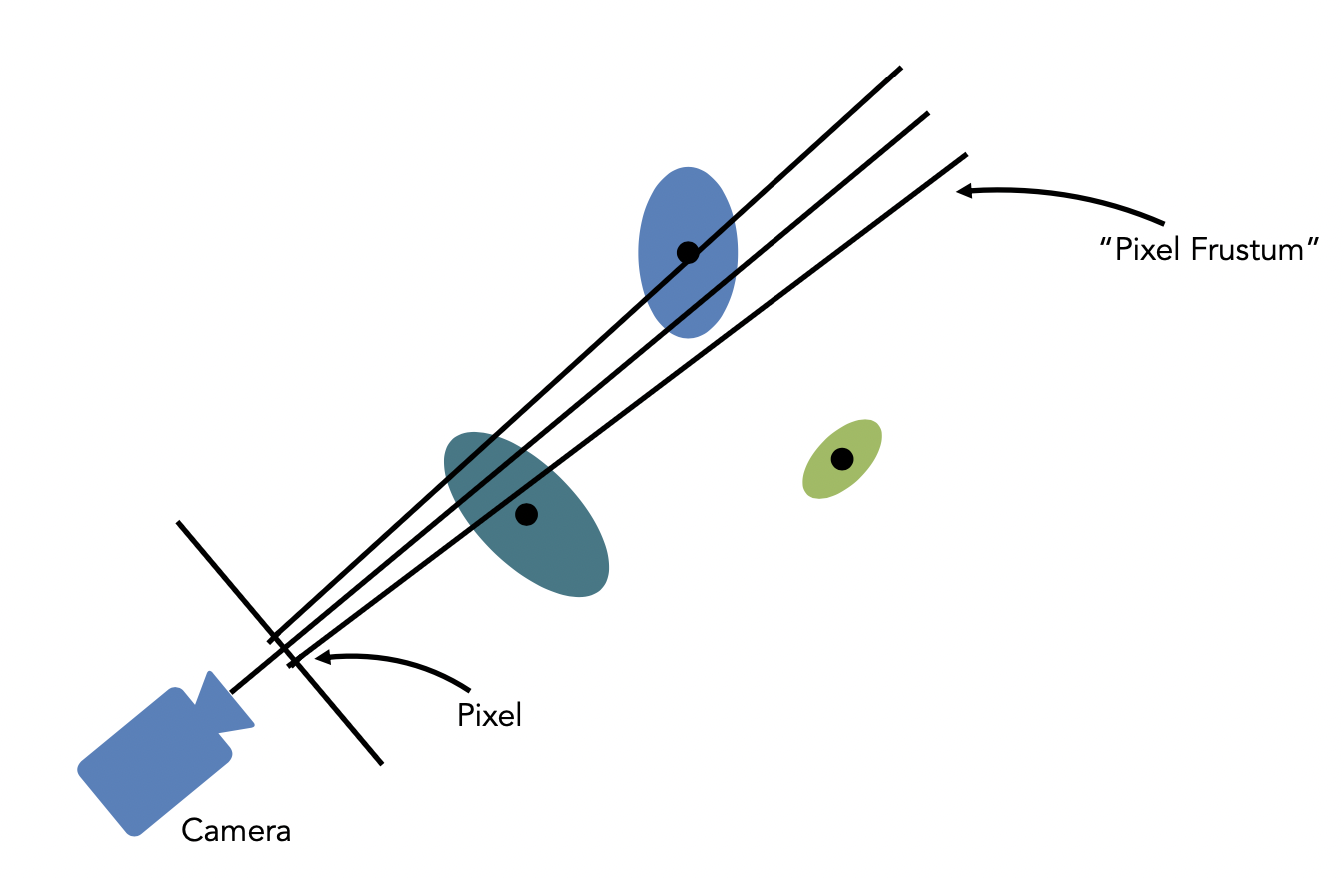
cam,pixel,frustum

(2) Gaussian Initialization, SortByKeys

가우시안들에 대해 view space depth와 tile ID를 합친 key를 부여하고, 이를 활용하여 Radix sort 알고리즘을 적용합니다. 해당 Sorting 알고리즘을 통해 depth 순으로 가우시안들이 정렬되는 $\alpha$ -blending이 구현됩니다.

7. Results

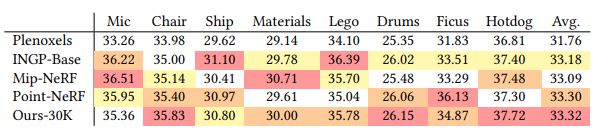
다른 NeRF모델들과의 PSNR 비교 테이블입니다. 몇몇 데이터셋에 대해 가장 높은 score를 기록하고 있습니다. 평균 PSNR이 가장 높은 것도 살펴볼 만합니다.

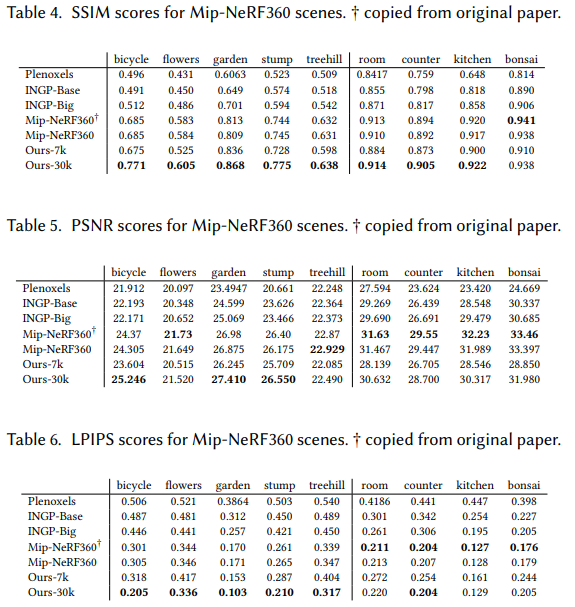
Mip-NeRF360 scenes에 대해 3D GS와의 metric 비교 테이블입니다. 많은 scene들에서 SOTA를 달성하였으며, Mip-NeRF360이 더 높은 metric을 보여줄 때에도 퀄리티에서 큰 차이를 보이지 않습니다.

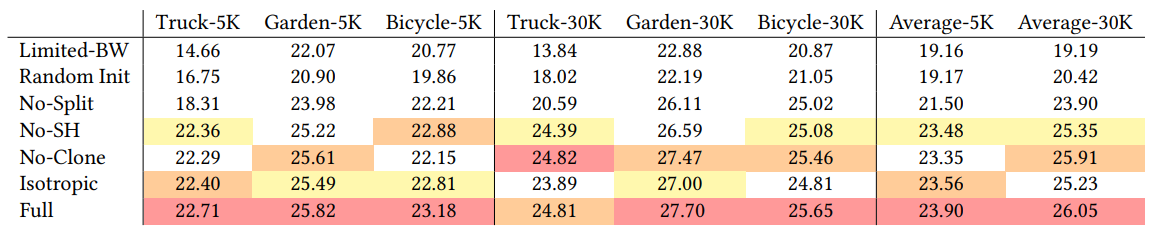
각 method에 대한 Ablation study입니다. SFM으로부터 initialization하는 것과 Adpative control에서 Split을 적용하는 것이 최적화에 큰 영향을 주고 있었습니다.

Appendix

$\alpha$ -blending

Blending은 물체의 투명도를 구현하는 기술입니다. 물체 자체와 그 뒤에 존재하는 물체들의 색이 혼합되어 투명도가 표현됩니다.

좌우의 잔디 이미지는 OpenGL로 표현되었으며, 투명도 고려 전(왼쪽)과 후(오른쪽)의 차이를 보여줍니다.

Blending을 적용할 때는 다음의 식이 적용됩니다.

\bar{C}_\text{result} = \bar{C}_\text{source} * {F}_\text{source} + \bar{C}_\text{destination} * {F}_\text{destination}

$\bar{C}_\text{source}$ : source color vector(반투명 물체)
$\bar{C}_\text{destination}$ : destination color vector
${F}_\text{source}$ : source vector value, source 컬러에 대한 alpha 값의 적용 정도
${F}_\text{destination}$ : destination vector value, destination 컬러에 대한 alpha 값의 적용 정도

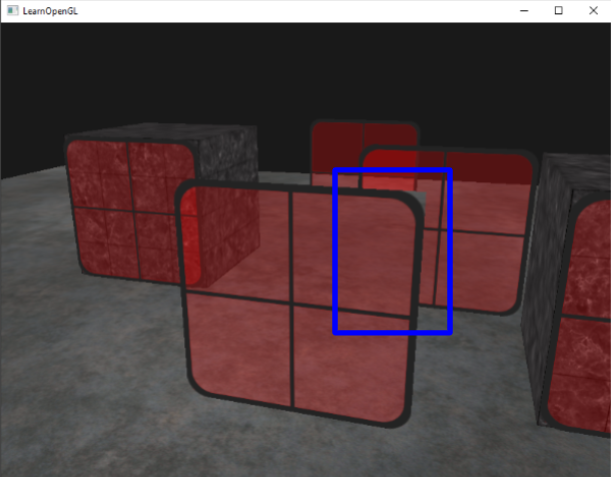
하지만 위에서 언급한 단계들만 적용하였을 때 사진과 같은 문제가 발생합니다. depth 고려가 blending과 동시에 이루어지지 않아 앞의 불투명한 유리창이 뒤에 있는 유리창을 가려버린 것입니다. (원래라면 앞의 유리를 통해 뒤의 유리가 보여야 할 것 입니다.)

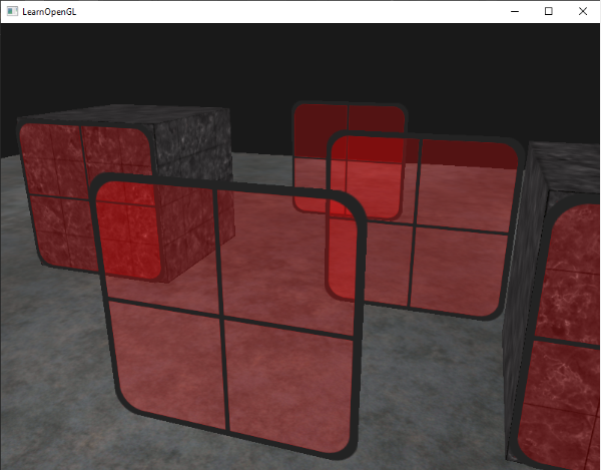
따라서 다음의 순서로 blending이 진행됩니다.

불투명한 물체를 먼저 그립니다.
모든 투명한 물체를 정렬합니다.
정렬된 순서대로 투명한 물체를 그립니다. (뒤에 있는 물체부터 그립니다.)

정렬 알고리즘: camera 위치 벡터와 object 위치 벡터 사이의 거리 값을 key로 지정한 후, key에 따라 정렬합니다.

(+update!) in GS rasterization

Gaussian Splatting의 rasterization 코드에서는, depth 값을 오름차순으로 정렬합니다.

즉, (depth 값이 작은) 카메라와 가까운 가우시안부터 렌더링이 이루어집니다.
cub::DeviceRadixSort::SortPairs(d_temp_storage,
								temp_storage_bytes,
								d_keys_in, d_keys_out,
								d_values_in, d_values_out,
								num_items);
// d_keys_out            <-- [0, 3, 5, 6, 7, 8, 9]
// d_values_out          <-- [5, 4, 3, 1, 2, 0, 6]

Spherical Harmonic (SH)

Spherical Harmonics(구면 조화 함수)는 구의 표면에서 정의된 함수입니다. NeRF 분야에서 SH를 사용하는 이유는 그림에서와 같이 view-dependent( $\theta, \phi$ ) color 값을 표현하는 데에 사용됩니다.

Y^m_l(\theta,\phi) = N\exp(im\phi)P^m_l(\cos\theta)

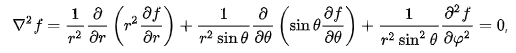
위의 라플라스 방정식 해를 구면좌표계에서 해결하면 구면 조화 함수 $Y_m^l$ 을 얻을 수 있습니다. 구면 좌표계가 $(r, \theta, \phi)$ 로 이루어져 있는데, 원점에서의 거리 $r$ 을 제외한 z축과 이루는 각도 (위아래) $\theta$ 와 z축을 중심으로 x축과 이루는 각도(좌우) $\phi$ 로 해당 함수를 표현할 수 있습니다.

$l$ 에 따른 구면 조화 함수 table입니다. $m$ 은 $-l$ ~ $l$ 의 범위로 조정됩니다. [Table of spherical harmonics - Wikipedia]

C = \sum^{l_{max}}_{l=0}\sum^l_{-l} k \cdot Y_l^m

SH를 통해서 color 값을 얻어내는 식입니다. coefficients $k$ 와 weighted sum을 하여 구해집니다. max degree인 $l_{max}$ 는 초기에 설정됩니다.

Reference

[1][Bernhard Kerbl](https://scholar.google.at/citations?user=jeasMB0AAAAJ&hl=en), Georgios Kopanas, 3D Gaussian Splatting for Real-Time Radiance Field Rendering, https://arxiv.org/pdf/2308.04079
[2] gaussian-splatting Github, https://github.com/graphdeco-inria/gaussian-splatting
[3] openGL, $\alpha$ -blending, https://learnopengl.com/Advanced-OpenGL/Blending
[4] wikipedia, 구면 조화 함수 - 위키백과, 우리 모두의 백과사전 (wikipedia.org)
[5] EWA Splatting paper, https://www.cs.umd.edu/~zwicker/publications/EWASplatting-TVCG02.pdf
[6] CS231a slide (image로 사용)

개인적 회고

기존에 게시했던 Gaussian Splatting에 대한 주요 내용 보완과, tile-based rasterization에 대한 내용을 해당 포스트에 합치는 과정을 진행하였습니다. GS에 관련한 내용들을 앞으로도 자주 포스팅할 예정입니다.

김민솔

Interested in Vision, Generative, Neural Rendering

다음 포스트

3D Gaussian Splatting

Gaussian-Splatting