DDPM(Denoising Diffusion Probabilistic Models)은 adversarial training 없이(GAN 계열 모델 x) 이미지 생성 분야에서 좋은 성능을 보였습니다. 하지만, 샘플링 과정에서 Markov chain이 사용되기 때문에 매우 많은 시간이 소요됩니다. 따라서 DDIM(Denoising Diffusion Implicit Models)에서는 Non-Markovian process 로 같은 목적 함수를 사용하여 샘플링하는 방법을 고려하였습니다. 이에 대해서 간단하게 살펴보겠습니다.
본 포스트는 DDPM에 대한 기본적인 이해도가 있다는 가정 하에 작성되었습니다.
Back to DDPM !
Loss function
L s i m p l e ( θ ) : = E t , x 0 , ϵ [ ∣ ∣ ϵ − ϵ θ ( α t ‾ x 0 + 1 − α t ‾ ϵ , t ) ∣ ∣ 2 ] L_{simple}(\theta) := \mathbb{E}_{t, \mathbf{x}_0, \epsilon}[||\epsilon - \epsilon_\theta(\sqrt{\overline{\alpha_t}}\mathbf{x}_0 + \sqrt{1 - \overline{\alpha_t}}\epsilon, t)||^2] L s i m p l e ( θ ) : = E t , x 0 , ϵ [ ∣ ∣ ϵ − ϵ θ ( α t x 0 + 1 − α t ϵ , t ) ∣ ∣ 2 ] DDIM의 핵심은 DDPM에서와 같은 Objective function으로 샘플링이 가능하게 설계하는 것입니다. (같은 목적 함수로 설계되었기 때문에, pretrained DDPM 모델에 DDIM 샘플링을 적용하는 것이 가능합니다! )
따라서 DDIM 샘플러를 설계하기 위해서는, DDPM에서의 Forward process에서 가지는 ①diffusion 커널, ②posterior, ③posterior mean 총 3가지의 조건을 만족하는 Forward process의 familiy 를 찾아야 합니다.
위에서 언급한 3가지 조건 수식을 아래에서 소개한 후에, Non-Markovian process에 대해서 살펴보겠습니다.
Diffusion Kernel
q ( x t ∣ x 0 ) = N ( x t ; α t ‾ x 0 , ( 1 − α t ‾ ) I ) q(\mathbf{x}_t|\mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_{t};\sqrt{\overline{\alpha_t}}\mathbf{x}_{0}, (1-\overline{\alpha_t})\mathbf{I}) q ( x t ∣ x 0 ) = N ( x t ; α t x 0 , ( 1 − α t ) I )
α t ‾ = ∏ s = 1 t ( 1 − β s ) \overline{\alpha_t} = \prod^t_{s=1} (1 - \beta_s) α t = ∏ s = 1 t ( 1 − β s ) x t = α t ‾ x 0 + ( 1 − α t ‾ ) ϵ \mathbf{x}_t = \sqrt{\overline{\alpha_t}}\mathbf{x}_{0} + \sqrt{(1-\overline{\alpha_t})}\epsilon x t = α t x 0 + ( 1 − α t ) ϵ
Forward process(posterior)
q ( x t − 1 ∣ x T , x 0 ) = N ( x t − 1 ; μ ~ t ( x t , x 0 ) , σ ~ t 2 I ) q(\mathbf{x}_{t-1}|\mathbf{x}_T, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde\mu_t(\mathbf{x}_t, \mathbf{x}_0), \tilde\sigma^2_t\mathbf{I}) q ( x t − 1 ∣ x T , x 0 ) = N ( x t − 1 ; μ ~ t ( x t , x 0 ) , σ ~ t 2 I )
μ ~ t ( x t , x 0 ) = a x t + b ϵ = a x t + b x t − α ‾ t x 0 1 − α ‾ t \tilde\mu_t(\mathbf{x}_t, \mathbf{x}_0) = a\mathbf{x}_t + b\epsilon = a\mathbf{x}_t + b\frac {\mathbf{x}_t - \sqrt{\overline{\alpha}_{t}}\mathbf{x}_0} {\sqrt{1 - \overline{\alpha}_{t}}} μ ~ t ( x t , x 0 ) = a x t + b ϵ = a x t + b 1 − α t x t − α t x 0
Reverse process
p θ ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ θ ( x t , t ) , σ ~ t 2 I ) p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \tilde\sigma^2_t\mathbf{I}) p θ ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ θ ( x t , t ) , σ ~ t 2 I )
μ θ ( x t , t ) = a x t + b ϵ θ ( x t , t ) = a x t + b x t − α ‾ t x ^ 0 1 − α ‾ t \mu_\theta(\mathbf{x}_t, t) = a\mathbf{x}_t + b\epsilon_\theta(\mathbf{x}_t, t) = a\mathbf{x}_t + b\frac {\mathbf{x}_t - \sqrt{\overline{\alpha}_{t}} \hat{\mathbf{x}}_0} {\sqrt{1 - \overline{\alpha}_{t}}} μ θ ( x t , t ) = a x t + b ϵ θ ( x t , t ) = a x t + b 1 − α t x t − α t x ^ 0
Variational Inference for Non-Markovian Forward process
Forward process(posterior)
q ( x t − 1 ∣ x t , x 0 ) = N ( α ‾ t − 1 x 0 + 1 − α ‾ t − 1 − σ ~ t 2 ⋅ x t − α ‾ t x 0 1 − α ‾ t , σ ~ t 2 I ) q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\sqrt {\overline{\alpha}_{t-1}} \mathbf{x}_0 + \sqrt {1 - \overline{\alpha}_{t-1} - \tilde\sigma^2_t} \cdot \frac {\mathbf{x}_t - \sqrt{\overline{\alpha}_{t}} {\mathbf{x}}_0} {\sqrt{1 - \overline{\alpha}_{t}}} , \tilde\sigma^2_t\mathbf{I}) q ( x t − 1 ∣ x t , x 0 ) = N ( α t − 1 x 0 + 1 − α t − 1 − σ ~ t 2 ⋅ 1 − α t x t − α t x 0 , σ ~ t 2 I ) Reverse process
p ( x t − 1 ∣ x t ) = N ( α ‾ t − 1 x ^ 0 + 1 − α ‾ t − 1 − σ ~ t 2 ⋅ x t − α ‾ t x ^ 0 1 − α ‾ t , σ ~ t 2 I ) p(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\sqrt {\overline{\alpha}_{t-1}} \hat{\mathbf{x}}_0 + \sqrt {1 - \overline{\alpha}_{t-1} - \tilde\sigma^2_t} \cdot \frac {\mathbf{x}_t - \sqrt{\overline{\alpha}_{t}} \hat{\mathbf{x}}_0} {\sqrt{1 - \overline{\alpha}_{t}}} , \tilde\sigma^2_t\mathbf{I}) p ( x t − 1 ∣ x t ) = N ( α t − 1 x ^ 0 + 1 − α t − 1 − σ ~ t 2 ⋅ 1 − α t x t − α t x ^ 0 , σ ~ t 2 I ) Forward process의 3가지 조건을 만족하는 Non-Markovian process와 이에 따른 Reverse process입니다. 이 친구들을 활용하여 샘플링 과정까지 알아보겠습니다.
Sampling from Generalized Generative Processes
위에서 정의한 process에 의해서 denoised observation 을 다음과 같이 정의할 수 있습니다.
f θ ( t ) ( x t ) : = ( x t − 1 − α ‾ t ⋅ ϵ θ ( t ) ( x t ) α ‾ t f^{(t)}_\theta(\mathbf{x}_t) := \frac {(\mathbf{x}_t - \sqrt {1 - \overline{\alpha}_t } \cdot \epsilon^{(t)}_\theta(\mathbf{x}_t)} {\sqrt {\overline{\alpha}_t}} f θ ( t ) ( x t ) : = α t ( x t − 1 − α t ⋅ ϵ θ ( t ) ( x t )
Reparameterization trick을 변형하여 유도된 것입니다! (x t = α t ‾ x 0 + ( 1 − α t ‾ ) ϵ \mathbf{x}_t = \sqrt{\overline{\alpha_t}}\mathbf{x}_{0} + \sqrt{(1-\overline{\alpha_t})}\epsilon x t = α t x 0 + ( 1 − α t ) ϵ
이를 통해 generative process를 정리하면 다음과 같습니다.
p θ ( t ) ( x t − 1 ∣ x t ) = { N ( f θ ( 1 ) ( x 1 ) , σ 1 2 I ) if t = 1 q σ ( x t − 1 ∣ x t , f θ ( t ) ( x t ) ) otherwise, p^{(t)}_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) = \begin{cases} \mathcal{N}(f^{(1)}_\theta(\mathbf{x}_{1}), \sigma^2_1\mathbf{I}) &\text{if } t=1 \\ q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, f^{(t)}_\theta(\mathbf{x}_t)) &\text{otherwise, } \end{cases} p θ ( t ) ( x t − 1 ∣ x t ) = { N ( f θ ( 1 ) ( x 1 ) , σ 1 2 I ) q σ ( x t − 1 ∣ x t , f θ ( t ) ( x t ) ) if t = 1 otherwise, generative process로 구한 p θ ( x 1 : T ) p_\theta(\mathbf{x}_{1:T}) p θ ( x 1 : T ) x t − 1 \mathbf{x}_{t-1} x t − 1 x t \mathbf{x}_{t} x t
x t − 1 = α ‾ t − 1 ( ( x t − 1 − α ‾ t ⋅ ϵ θ ( t ) ( x t ) α ‾ t ) + 1 − α ‾ t − 1 − σ t 2 ⋅ ϵ θ ( t ) ( x t ) + σ t ϵ t \mathbf{x}_{t-1} = \sqrt {\overline{\alpha}_{t-1}}\Big( \frac {(\mathbf{x}_t - \sqrt {1 - \overline{\alpha}_t } \cdot \epsilon^{(t)}_\theta(\mathbf{x}_t)} {\sqrt {\overline{\alpha}_t}} \Big) + \sqrt {1 - \overline{\alpha}_{t-1} - \sigma^2_t}\cdot \epsilon^{(t)}_\theta(\mathbf{x}_t) + \sigma_t\epsilon_t x t − 1 = α t − 1 ( α t ( x t − 1 − α t ⋅ ϵ θ ( t ) ( x t ) ) + 1 − α t − 1 − σ t 2 ⋅ ϵ θ ( t ) ( x t ) + σ t ϵ t
predicted x 0 \mathbf{x}_{0} x 0 ( x t − 1 − α ‾ t ⋅ ϵ θ ( t ) ( x t ) α ‾ t \frac {(\mathbf{x}_t - \sqrt {1 - \overline{\alpha}_t } \cdot \epsilon^{(t)}_\theta(\mathbf{x}_t)} {\sqrt {\overline{\alpha}_t}} α t ( x t − 1 − α t ⋅ ϵ θ ( t ) ( x t )
direction pointing to x t \mathbf{x}_{t} x t 1 − α ‾ t − 1 − σ t 2 ⋅ ϵ θ ( t ) ( x t ) \sqrt {1 - \overline{\alpha}_{t-1} - \sigma^2_t}\cdot \epsilon^{(t)}_\theta(\mathbf{x}_t) 1 − α t − 1 − σ t 2 ⋅ ϵ θ ( t ) ( x t )
random noise: σ t ϵ t \sigma_t\epsilon_t σ t ϵ t
이때 모든 t t t σ ~ t 2 = 0 \tilde\sigma^2_t =0 σ ~ t 2 = 0 x t → x 0 \mathbf{x}_{t} \rightarrow \mathbf{x}_{0} x t → x 0 DDIM sampler 입니다.
ODE interpretation
x t − Δ t α ‾ t − Δ t = x t α ‾ t + ( 1 − α ‾ t − Δ t α ‾ t − Δ t − 1 − α ‾ t α ‾ t ) ϵ θ ( t ) ( x t ) \frac {\mathbf{x}_{t-\Delta t}} {\sqrt{\overline{\alpha}_{t-\Delta t}}} = \frac {\mathbf{x}_{t}} {\sqrt{\overline{\alpha}_{t}}} + \Big(\sqrt {\frac {1 - {\overline{\alpha}_{t-\Delta t}}} {{\overline{\alpha}_{t-\Delta t}}}} - \sqrt{\frac {1 - {\overline{\alpha}_{t}}} {\overline{\alpha}_{t}}} \Big) \epsilon^{(t)}_\theta(\mathbf{x}_t) α t − Δ t x t − Δ t = α t x t + ( α t − Δ t 1 − α t − Δ t − α t 1 − α t ) ϵ θ ( t ) ( x t )
generative process sampling 식을 ODE 형식으로 바꾼 식입니다.
DDIM의 샘플링 과정을 ODE로 나타낸 것입니다. (σ = 0 \sigma=0 σ = 0
d x ‾ ( t ) = ϵ θ ( t ) ( x ‾ ( t ) σ 2 + 1 ) d σ ( t ) d\overline{\mathbf{x}}(t) = \epsilon^{(t)}_\theta \Big(\frac {\overline{\mathbf{x}}(t)} {\sqrt {\sigma^2 + 1}} \Big) d\sigma(t) d x ( t ) = ϵ θ ( t ) ( σ 2 + 1 x ( t ) ) d σ ( t )
reparameterization: 1 − α ‾ α ‾ → σ \sqrt{\frac {1 - {\overline{\alpha}_{}}} {\overline{\alpha}_{}}} \rightarrow \sigma α 1 − α → σ x α ‾ → x ‾ \frac {\mathbf{x}} {\sqrt{\overline{\alpha}}} \rightarrow \overline{\mathbf{x}} α x → x \frac {} {}
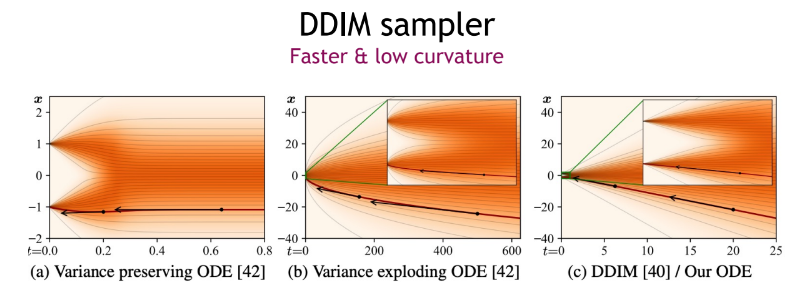
이처럼, DDIM을 하나의 ODE로 바라보는 것도 가능합니다. 또한 최적의 mode를 가질 때 해당 ODE가 “variance exploding ” SDE의 probability flow ODE 가 됩니다.
그림을 통해 ODE들을 확인해보면, DDIM ODE가 비교적 더 적은 곡률을 가지고 대체로 선형의 궤적을 지니는 것을 볼 수 있습니다. 이를 통해 DDIM ODE가 가지는 장점은 다음과 같습니다.
더 적은 truncation errors(근사치 추정 오류)를 가진다.
샘플링 속도가 더 빨라진다.
Experiments
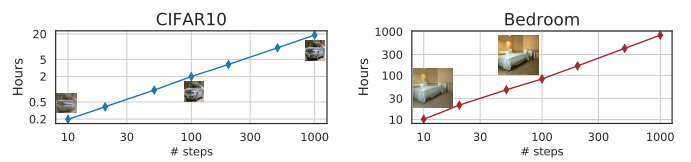
DDIM은 적은 iteration을 사용하였을 때 DDPM보다 좋은 샘플 퀄리티를 낼 뿐만 아니라 샘플링 속도도 약 10배에서 50배까지 오르는 것을 확인할 수 있습니다.
σ τ i ( η ) = η ( 1 − α τ i − 1 ) / ( 1 − α τ i ) 1 − α τ i / α τ i − 1 \sigma_{\tau_i}(\eta) = \eta\sqrt{(1 - \alpha_{\tau_{i-1}}) / (1 - \alpha_{\tau_{i}})}\sqrt{1 - \alpha_{\tau_{i}}/ \alpha_{\tau_{i-1}}} σ τ i ( η ) = η ( 1 − α τ i − 1 ) / ( 1 − α τ i ) 1 − α τ i / α τ i − 1
σ ^ = 1 − α τ i / α τ i − 1 \hat \sigma = \sqrt{1 - \alpha_{\tau_{i}}/ \alpha_{\tau_{i-1}}} σ ^ = 1 − α τ i / α τ i − 1
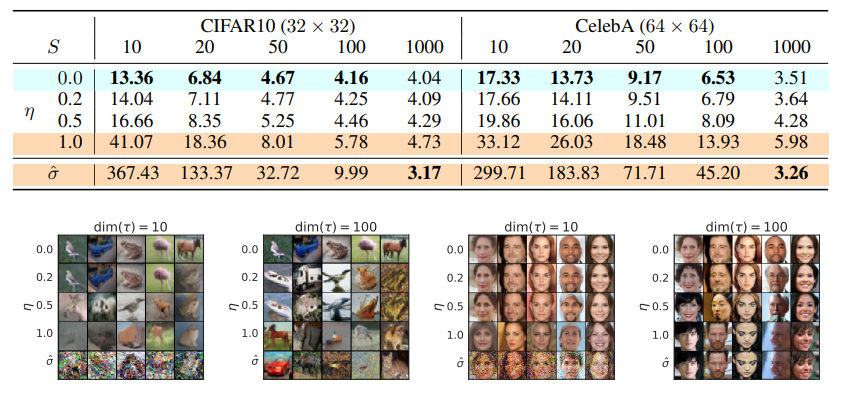
η = 1.0 \eta = 1.0 η = 1 . 0 σ ^ \hat \sigma σ ^ η \eta η η = 0. \eta = 0. η = 0 .
CIFAR10과 CelebA 데이터셋 모두에서 η \eta η FID score를 가지는 것을 확인할 수 있습니다. 또한 steps 수가 1000일 때도 DDIM과 DDPM의 FID 값이 큰 차이를 보이지 않는 점도 주목할 만합니다.
Nvidia 2080 Ti GPU를 사용하였을 때 sampling steps에 따라 50K images를 생성하는 속도를 비교한 그래프입니다. 적은 steps를 사용할 수록 1000 steps에 비해 약 10배 ~ 50배 빠른 DDIM의 샘플링 속도를 확인할 수 있습니다.
Progressive distillation
DDIM sampler를 하나의 증류 방식으로 고안한 모델입니다. “student” 모델이 인접한 두 샘플링 스텝을 학습하고, 이를 “teacher” 모델에서의 한 스텝이 되게 합니다. distillation stage가 지나면서 “student” 모델을 새로운 “teacher” 모델로 만들어가는 학습 방법입니다.
Algorithm
일반적인 diffusion training과 Progressive distillation의 알고리즘을 비교해보겠습니다. 일반적인 diffusion 학습에서는 data, time, noise를 샘플링하고 이를 diffusion한 후에 Loss로 최적화를 진행합니다. Progressive distillation 에서는 ① t를 “student”의 수만큼 나누어 샘플링하고, ② 각각 diffusion step을 적용한 후 ③ “teacher” x ^ \hat x x ^
FID
Generatice model로 생성된 이미지를 평가하기 위해 사용하는 이미지 비교 방식은 크게 두 가지가 있습니다. 바로 Pixel distance 와 Feature distance 입니다. Pixel distance 는 두 이미지의 픽셀 값을 이용한 거리 측정 방식입니다. 이는 매우 간단하기 때문에 신뢰성이 떨어집니다. Feature distance 는 두 이미지를 inception model의 통과시켜 추출한 피쳐 간의 mean과 covariance를 계산하여 두 분포의 거리를 측정하는 방식입니다. 실제 data dist.와 가짜 data dist. 간의 유사도를 비교하는 방식으로, 현재도 널리 사용되는 이미지 평가 metric입니다.
F I D = ∣ ∣ μ X − μ Y ∣ ∣ 2 2 − T r ( Σ X + Σ Y − 2 Σ X Σ Y ) FID=∣∣\mu_X−\mu_Y∣∣^2_2−Tr(\Sigma_X+\Sigma_Y−2\Sigma_X\Sigma_Y) F I D = ∣ ∣ μ X − μ Y ∣ ∣ 2 2 − T r ( Σ X + Σ Y − 2 Σ X Σ Y ) Reference
[1] Jiaming Song, Chenlin Meng & Stefano Ermon, Denoising Diffusion Implicit Models, 2010.02502.pdf (arxiv.org)
[2] Ruiqi Gao(https://ruiqigao.github.io/ ), “Tutorial on Denoising Diffusion-based Generative Modeling: Foundations and Applications” (in CVPR 2022), Denoising Diffusion-based Generative Modeling: Foundations and Applications (cvpr2022-tutorial-diffusion-models.github.io)
[3] Tim Salimans & Jonathan Ho, Progressive Distillation for Fast Sampling of Diffusion Models, 2202.00512.pdf (arxiv.org)