Score-based Generative modeling with DEs

ICLR 2021에 기재된 논문인 Score-based Genererative Modeling Through Stochastic Differential Equations을 중심으로 미분방정식(Diffential Equations)을 통해 generative modeling(데이터 → 노이즈 → 데이터)을 해결하는 과정을 알아보겠습니다. 저자들은 SDE(stochastic differential equation)를 통해 복잡한 데이터 분포를 우리가 아는 사전 분포(std)로 부드럽게 전환합니다. 또한 reverse-time SDE를 통해 prior dist.를 data dist.로 되돌리는데, 이때 score의 개념이 사용됩니다. 본격적으로 알아보기 전, 미분방정식에 대해 먼저 살펴보겠습니다.

Differential Equations

미분 방정식(DE)에는 여러 종류가 존재하지만, 이번 포스트에서 주로 살펴볼 것은 상미분방정식(Ordinary DE)과 확률미분방정식(Stochastic DE)입니다.

ODE

• $x$: 관심 있는 대상 i.e. value of pixel in an image
• $t$: 시간 변수
• $f$: $x$의 변화를 나타내는 함수 / Neural Network
• Analytical Solution: $x(t) = x(0) \int^t_0f(x,\tau)d\tau$
• Iterative Numerical Solution: $x(t + \Delta t) \approx x(t)+ f(x(t),t)\Delta t$

ODE는 하나의 독립 변수를 갖는 함수를 해결하는 미분방정식입니다. 위 그래프에서 보이는 실선이 x의 경로를 생성하는 $f$입니다. 아래에서 보게 될 SDE와 다른 점은, deterministic하다는 점입니다.

SDE

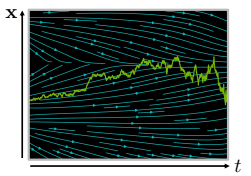
• $w_t$: Wiener Process (Gaussian White noise 주입하는 역할!)
• $f(x,t)$: drift coefficient
• $\sigma(x,t)w_t$: diffusion coefficient
• Iterative Numerical Solution: $x(t + \Delta t) \approx x(t)+ f(x(t),t)\Delta t + \sigma(x(t),t)\sqrt{\Delta t}\mathcal{N}(0, \mathbf{I})$

위에서 봤던 ODE에서 diffusion term이 추가된 형태입니다. 즉, ODE에서와 같이 deterministic하게 작용하지 않고, Gaussian noise를 통해 랜덤성이 부여되어 각 timestep에서 $x$의 state를 더 부드럽게 update하는 것이 가능합니다.

Forward diffusion process

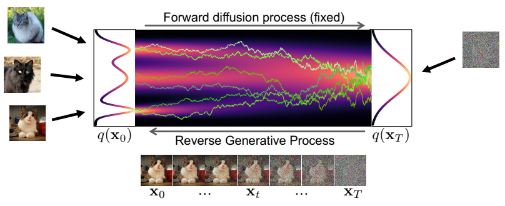
Forward process를 통해서 data dist.를 std로 변화시킵니다. 사진과 같이 SDE를 활용하여 Forward를 진행 시 jitter가 생기는 부분이 diffusion term을 통해서 만들어진 것입니다.

• drift term: $- \frac 1 2 \beta(t)\mathbf{x}_tdt$ / pulls toward mode(zero)
• diffusion term: $\sqrt {\beta(t)}dw_t$ / injects noise

Reverse generative diffusion process

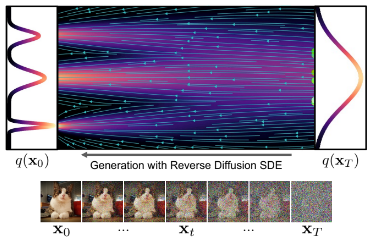
Reverse process에서는 noise로부터 data를 생성하는 작업이 이루어집니다. Forward process와 똑같은 확률 분포를 따라가게 되며, 차이점은 score function을 도입한 점입니다.

• score function: $\nabla_{\mathbf{x}_t} \log {q_t(\mathbf{x}_t)}$

score function을 구하기 위한 방법으로 model을 사용하는 것이 있습니다. (DDPM에서 사용했던 방법입니다!)

• $t$: diffusion time
• $\mathbf{x}_t$: diffused data
• $s_\theta(\mathbf{x}_t, t)$: neural network
• $\nabla_{\mathbf{x}_t}\log{q_t(\mathbf{x}_t)}$: score of diffused data(marginal dist.)

하지만, score에서 $q_t(\mathbf{x}_t)$ 부분이 intractable하기 때문에 score function을 구하는 것이 불가능해집니다.

Denoising score matching

marginal dist.로 score matching을 하지 않고, 독립적인 데이터 $x_0$에 diffuse하여 score function을 구하여 적분 문제를 해결합니다. 즉 diffusion 시 적용된 noise를 예측하는 방향으로 학습이 진행됩니다.

• $\gamma_t$: $\exp\{- \frac 1 2 \int^t_0 \beta(s)ds \}$
• $\sigma^2_t$: $1 - \exp\{- \frac 1 2 \int^t_0 \beta(s)ds \}$ → “variance preserving”

Objective function

• $\mathbf{x}_t \sim q_t(\mathbf{x}_t|\mathbf{x}_0)$
• $\nabla_{\mathbf{x}_t}\log{q_t(\mathbf{x}_t|\mathbf{x}_0)}$: score of diffused data sample

최종적으로 구한 Objective function은 다음과 같습니다. marginal dist.의 score를 직접 구하는 것이 불가능하므로, diffused data sample dist.의 score를 통해 근사하는 방법을 사용합니다.

기타 수식 전개

우리는 diffused data sample dist.를 알고 있으므로 이의 score를 다음과 같이 구할 수 있습니다. 따라서 neural network 역시 표현하는 것이 가능해집니다.

• neural network: $s_\theta(\mathbf{x}, t) \simeq - \frac {\epsilon_\theta(\mathbf{x}, t)} {\sigma_t}$

최종적으로 Loss function을 표현하면 다음과 같습니다.

SDE를 통하여 generative modeling을 하였을 때 DDPM과 같은 종류의 diffusion model이 도출된 것을 확인할 수 있습니다. 단, 여기서는 discrete time이 아닌 continuous time을 사용했다는 점이 중요한 차이점이 되겠네요.

Probability ODE

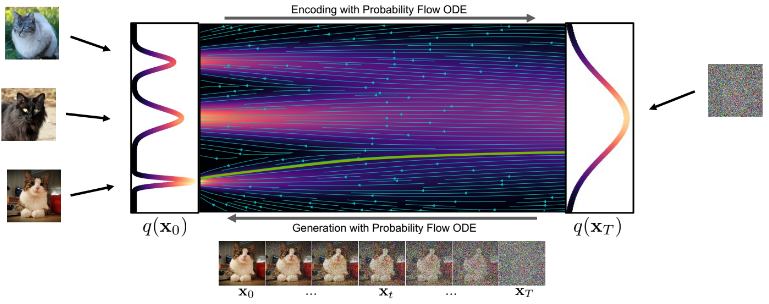
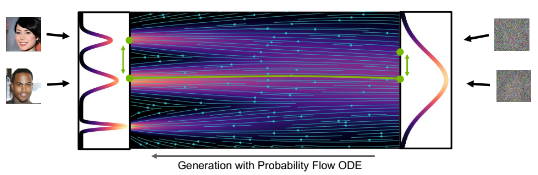
Probability ODE는 SDE에서와 같은 $q_t(\mathbf{x}_t)$를 deterministic한 방법을 통해 얻어내는 방법입니다. 초기 노이즈를 std에서 뽑은 후 data를 반복해서 생성하면(reverse process) 어떤 data 분포를 얻게 되는데, 이는 generative diffusion SDE로 얻는 분포와 동일합니다. 초기 노이즈를 std에서 대량으로 뽑은 후 data generalization하게 되면, 결국 data 분포에서 샘플링됩니다. 이 data 분포는 gneerative diffusion SDE로 얻는 분포와 동일하기 때문에 Probability ODE와 SDE가 동일하다고 볼 수 있습니다.

• SDE에 비해서 더 직선적으로 data 분포의 mode로 향하는 것을 확인할 수 있습니다.

SDE vs Probability ODE

SDE의 특징

1. solver: Euler-Maruyama
2. ODE에 비해 error correction 성능이 좋음.
3. 샘플링 속도가 더 느리다는 단점이 있습니다.

Probability ODE의 특징

1. solver: Euler-method, but Higher-Order method
2. ODE 사용 시, SDE보다 방정식 solver 사용이 더 용이합니다.
3. Deterministic encoding과 decoding을 통해 semantic image interpolation이 가능합니다.
   -> latent space에서 연속적인 변화들로 data space에서 의미 있는 변화를 이끌어내는 것을 의미합니다.

4. Log-likelihood를 계산하는 것이 가능합니다. $\log {p_\theta(\mathbf{x}_0)} = \log {p_T(\mathbf{x}_t)} - \int^T_0 Tr(\frac 1 2 \beta(t)\frac {d}{d\mathbf{x}_t} [\mathbf{x}_t + s_\theta(\mathbf{x}_t,t)])dt$

Appendix

Score funciton

Generative modeling의 궁극적인 목표는, 데이터셋$\{\mathbf{x}_1, . . . , \mathbf{x}_N\}$이 지니는 확률 분포 $p(\mathbf{x})$를 피팅한 모델을 찾아내어서, 해당 분포로부터 새로운 데이터들을 생성해내는 것입니다. 그 중 많이 사용하는 방법인 Likelihood-based model 같은 경우는 pdf(probability density function)이나 pmf(probability mass function)을 직접적으로 모델링하는 방법에 해당됩니다.

• $\theta$: learnable parameter
• $p_\theta(\mathbf{x})$: pdf
• ${\mathbf{Z}_\theta}$: normalizing factor / $\int p_\theta(\mathbf{x})d\mathbf{x} = 1$
• $f_\theta(\mathbf{x})$: unnormalized probabilistic model (energy-based model)

위와 같은 pdf가 있다고 가정해보겠습니다. 우리는 maximum log-likelihood 방법을 통해서 위의 pdf를 학습할 수 있습니다.

이때 $p_\theta(\mathbf{x})$를 구하기 위해서는, $f_\theta(\mathbf{x})$에 맞는 normalizing factor ${\mathbf{Z}_\theta}$를 구해야 합니다. 구하는 방법은 크게 두 가지가 있습니다. (1) normalizing factor ${\mathbf{Z}_\theta}$가 적분 가능하도록 모델의 구조를 제한하는 방법(causal convolutions in AE 모델, invertible networks in NFMs)과 (2) normalizing factor ${\mathbf{Z}_\theta}$를 근사하여 구하는 방법(Variational Inference, MCMC sampling)입니다.

하지만 두 방법을 사용하지 않고, 즉 density function을 모델링하지 않고 그의 미분 형태인 score function을 모델링하는 방법이 score-based modeling입니다. $s_\theta \approx \log {p_\theta(\mathbf{x})}$

score-based 모델은 ground-truth data score와 score-based model 간의 l2 distance를 측정하는 Fisher divergence를 통하여 학습할 수 있습니다.

하지만 위에서도 언급한 것처럼, ground-truth data score인 $\nabla_{\mathbf{x}}\log{p(\mathbf{x})}$를 직접적으로 구하는 것이 불가능합니다. 학습을 진행하는 시점에선 data dist. $p(\mathbf{x})$를 모르는 상황이기 때문입니다. 따라서 ground-truth data score없이 Fisher divergence를 최소하하는 과정을 거쳐야 하고, 이를 score matching으로 정의하였습니다. score matching에 대해서는 이미 설명하였으니 해당 파트에선 생략하겠습니다!

Langevin dynamics

Langevin dynamics은 score function만으로 data dist. $p(\mathbf{x})$에서 MCMC 샘플링하는 기법입니다. trained score-based model인 $s_\theta \approx \log {p_\theta(\mathbf{x})}$가 존재하는 경우에, prior $\mathbf{x}_0 \sim \pi(\mathbf{x})$에서부터 iterative 샘플링하여 $\mathbf{x}_t$를 구할 수 있습니다.

Reference

[1] Score-based Genererative Modeling Through Stochastic Differential Equations https://arxiv.org/pdf/2011.13456.pdf

[2] Karsten Kreis (in CVPR 2022), “Tutorial on Denoising Diffusion-based Generative Modeling: Foundations and Applications”, https://youtu.be/cS6JQpEY9cs?si=-cmPEx_j23mi2v8q

[3] Yang Song’s blog, http://yang-song.net/blog/2021/score/

[4] Langevin dynamics, Wikipedia, https://en.wikipedia.org/wiki/Metropolis-adjusted_Langevin_algorithm