Instant Neural Graphics Primitives with a Multiresolution Hash Encoding

김민솔·2024년 5월 25일
Instant-ngpNeRF
1

NeRF

목록 보기
2/10

1. Introduction

Fully connected network를 사용한 Neural graphics 분야에서는 train과 inference에 많은 메모리와 시간이 사용된다는 것이 문제점이었습니다. Instant NGP는 multi-resolution hash encoding을 도입하여 이미지의 퀄리티는 유지한 채 cost를 대폭 줄이는 데 성공한 모델입니다.

Multi-resolution hash encoding의 장점

  • hash encoding을 통해 MLP가 처리하는 floating points의 수가 감소하였습니다.
  • hash table lookup의 시간 복잡도가 O(1)\mathcal{O}(1)로, 메모리 접근 연산 속도를 대폭 줄였습니다.

2. Related Work

Encoding

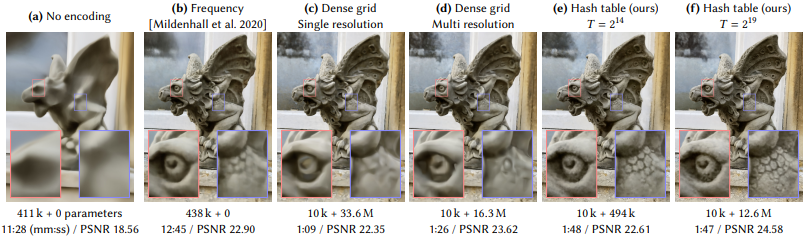
3d coordinates 좌표를 모델이 직접적으로 학습하면, 모델의 이미지의 공간 정보를 충분하게 학습하지 못합니다. (NeRF 논문에도 기재되어 있습니다.) 따라서 inputs을 고차원의 공간으로 매핑하는 encoding 기법이 사용됩니다. 아래는 Neural graphics에 사용되어 온 인코딩 기법들입니다.

Frequency encodings

Frequency encodings는 Transformer에서도 사용되는 인코딩 기법입니다. (Transformer에서는 token이 문맥을 갖도록 순차성을 부여하기 위해 사용되었습니다. 즉, 사용하는 이유가 Neural graphics 분야와는 다릅니다.)

enc(x)=(sin⁡(20x),sin⁡(21x),...sin⁡(2L−1x),cos⁡(20x),cos⁡(21x),...cos⁡(2L−1x))\text{enc}(x) = \big(\sin(2^0x), \sin(2^1x), ... \sin(2^{L-1}x), \\ \cos(2^0x), \cos(2^1x), ... \cos(2^{L-1}x) \big)

vanila NeRF에서 사용된 인코딩 기법이며, 해당 인코딩 기법 사용 시 cost가 매우 높은 것을 알 수 있습니다.

Parametric encodings

weights나 biases가 아닌 추가적인 trainable parameters를 도입하여 inputs을 인코딩하는 기법입니다. (grid, tree, …) 해당 인코딩 기법을 사용하면 파라미터의 수에 따라 메모리는 증가하지만 연산이 감소되는 효과를 가집니다.

Dense grid

Dense grid는 Neural net보다 더 많은 파라미터 수를 요구하는 Parametric encoding 기법입니다. Dense grid는 많은 피쳐들이 빈 공간에 할당된다는 점과, 밝은 부분에서의 근사 능력이 떨어진다(위 사진에서 확인 가능합니다.)는 단점을 갖고 있습니다.


3. Multi-resolution hash encoding

위의 테이블이 매우 중요합니다. level LL과 hash table size TT, feature dim FF, resolution NN을 확인하면서 인코딩 기법을 살펴보겠습니다.

아래에서 설명할 hash encoding 알고리즘에서 기재된 코드들은 Reference에 있는 HashNeRF-pytorch github에서 가져온 코드들입니다. (주석 일부는 추가하였습니다.)

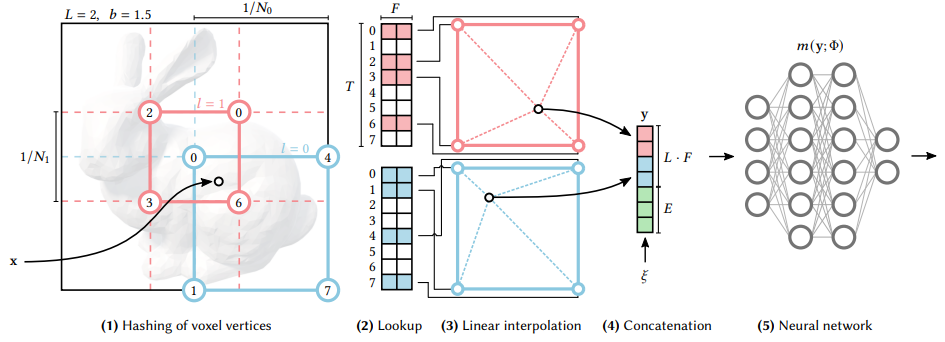
(1) Hashing of voxel vertices

Nl:=⌊Nmin⋅bl⌋b:=exp⁡(ln⁡Nmax−ln⁡NminL−1)N_l := ⌊N_{min}\cdot b^l⌋ \\ b:= \exp\Big(\frac {\ln N_{max} - \ln N_{min}} {L - 1} \Big)
  • NlN_l: resolution of level ll
  • bb: scale (level이 올라갈 때 resolution에 곱해지는 scale) / [1.26, 2] 사이에서 값 가짐
⌊xl⌋:=⌊x⋅Nl⌋⌈xl⌉:=⌈x⋅Nl⌉⌊\mathbf{x}_l⌋ := ⌊\mathbf{x}\cdot N_l⌋ \\ ⌈\mathbf{x}_l⌉ := ⌈\mathbf{x}\cdot N_l⌉
  • ⌊xl⌋⌊\mathbf{x}_l⌋: rounding down the inputs
  • ⌈xl⌉⌈\mathbf{x}_l⌉: rounding up the inputs

level에 맞는 resolution NlN_l에 해당하는NlN_l⌊xl⌋⌊\mathbf{x}_l⌋, ⌈xl⌉⌈\mathbf{x}_l⌉이 2d2^d개의 정수 vertice를 가지는 voxel을 생성합니다. 

BOX_OFFSETS = torch.tensor([[[i,j,k] for i in [0, 1] for j in [0, 1] for k in [0, 1]]],
                               device='cuda')

def get_voxel_vertices(xyz, bounding_box, resolution, log2_hashmap_size):
    '''
    xyz: 3D coordinates of samples. B x 3
    bounding_box: min and max x,y,z coordinates of object bbox (precomputed for each dataset)
    resolution: number of voxels per axis
    '''
    box_min, box_max = bounding_box # 입력 값으로 얻어옴.
		
    keep_mask = xyz==torch.max(torch.min(xyz, box_max), box_min)
    
    # bbox 값 넘어가는 xyz 좌표 값 전처리
    if not torch.all(xyz <= box_max) or not torch.all(xyz >= box_min):
        # print("ALERT: some points are outside bounding box. Clipping them!")
        xyz = torch.clamp(xyz, min=box_min, max=box_max)

    grid_size = (box_max-box_min)/resolution # grid 하나 당 가지는 크기 (사각형의 한 변)
    
    bottom_left_idx = torch.floor((xyz-box_min)/grid_size).int() # 좌표 값에 해당하는 grid의 최소 index
    voxel_min_vertex = bottom_left_idx*grid_size + box_min
    voxel_max_vertex = voxel_min_vertex + torch.tensor([1.0,1.0,1.0])*grid_size

    voxel_indices = bottom_left_idx.unsqueeze(1) + BOX_OFFSETS # voxel의 인덱스들을 박스 형태로 만듦, voxel의 각 코너에 해당됨!!
    hashed_voxel_indices = hash(voxel_indices, log2_hashmap_size) # hash function -> xyz 좌표에 해당하는 voxel의 index들 얻기

    return voxel_min_vertex, voxel_max_vertex, hashed_voxel_indices, keep_mask

(2) Lookup

이후 voxel의 각 코너를 level에 해당하는 feature vector 배열(size: TT)에 매핑시킵니다.

dense grid가 TT보다 적은 파라미터를 요구하는 경우에는(coarse levels) 1:1 매칭이 이루어집니다. 반대의 경우에는(finer levels) hash function h:Zd→ZTh : \mathbb{Z}^d \rightarrow \mathbb{Z}_T를 사용합니다. 이때 hash collision에 대한 처리는 이루어지지 않습니다. (Appendix에서 설명하겠습니다!!)

h(x)=(XORi=1dxiπi)mod  Th(\mathbf{x}) = \Big(\text{XOR}^d_{i=1} x_i\pi_i \Big) \mod T
  • πi\pi_i : large prime numbers
def hash(coords, log2_hashmap_size):
    '''
    coords: this function can process upto 7 dim coordinates
    log2T:  logarithm of T w.r.t 2
    '''
    primes = [1, 2654435761, 805459861, 3674653429, 2097192037, 1434869437, 2165219737] # pi (prime numbers)

    xor_result = torch.zeros_like(coords)[..., 0]
    for i in range(coords.shape[-1]):
        xor_result ^= coords[..., i]*primes[i] # B x 8

    return torch.tensor((1<<log2_hashmap_size)-1).to(xor_result.device) & xor_result # mod T
  • 마지막 mod 연산은 비트 연산입니다. 1<<size-1을 하게 되면, 111…1과 같은 값이 나타납니다. 여기에 xor 합과의 & 연산자를 적용하면 T로 나눈 나머지 값과 같은 값을 얻을 수 있게 됩니다.

(3) Linear interpolation

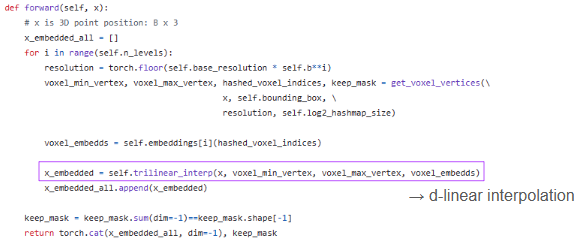
각 코너에 있는 feature vectors와 큐브 안에 있는 x\mathbf{x}와의 상대적인 거리를 이용하여 d-linear interpolation을 적용합니다. interpolation weight는 wl:= xl−⌊xl⌋\mathbf{w}_l :=\ \mathbf{x}_l - ⌊\mathbf{x}_l⌋입니다.

def trilinear_interp(self, x, voxel_min_vertex, voxel_max_vertex, voxel_embedds):
        '''
        x: B x 3
        voxel_min_vertex: B x 3
        voxel_max_vertex: B x 3
        voxel_embedds: B x 8 x 2
        '''
        # source: https://en.wikipedia.org/wiki/Trilinear_interpolation
        weights = (x - voxel_min_vertex)/(voxel_max_vertex-voxel_min_vertex) # B x 3

        # step 1
        # 0->000, 1->001, 2->010, 3->011, 4->100, 5->101, 6->110, 7->111
        c00 = voxel_embedds[:,0]*(1-weights[:,0][:,None]) + voxel_embedds[:,4]*weights[:,0][:,None]
        c01 = voxel_embedds[:,1]*(1-weights[:,0][:,None]) + voxel_embedds[:,5]*weights[:,0][:,None]
        c10 = voxel_embedds[:,2]*(1-weights[:,0][:,None]) + voxel_embedds[:,6]*weights[:,0][:,None]
        c11 = voxel_embedds[:,3]*(1-weights[:,0][:,None]) + voxel_embedds[:,7]*weights[:,0][:,None]

        # step 2
        c0 = c00*(1-weights[:,1][:,None]) + c10*weights[:,1][:,None]
        c1 = c01*(1-weights[:,1][:,None]) + c11*weights[:,1][:,None]

        # step 3
        c = c0*(1-weights[:,2][:,None]) + c1*weights[:,2][:,None]

        return c

(4) Concatenation, (5) MLP

각 레벨에 대한 feature vector와 auxiliary inputs를 concat한 후에 m(y;Φ)m(\mathbf{y};\Phi)에 input으로 전달하여 학습을 진행합니다. auxiliary inputs은 view direction(NeRF), textures(neural radiance caching)이 될 수 있습니다.


4. Implementation

instant ngp에서는 빠른 속도를 위해 tiny-cuda-nn framework를 사용하였습니다.

Architecture

  • NeRF를 제외하고는, 64 뉴런의 two-layer를 사용하였습니다. activation은 ReLU입니다.
  • NeRF의 구조는 5.4 NeRF에서 다루겠습니다.

Weight Initialization

  • network는 Xavier initialization, hash table은 uniform distribution U(−10−4,10−4)\mathcal{U}(-10^{-4}, 10^{-4})에서 초기화하는 방식을 채택하였습니다.

Training

  • optimizer로는 Adam을 사용하였고, network에 L2 정규화를 적용하였습니다.
  • gigapixel images, NeRF에는 L2 loss를 적용하였으며, SDF에는 MAPE를, NRC에는 luminance-relative L2 loss를 적용하였습니다.

Non-spatial input dimensions

빛에 따른 변화를 학습할 때 필요한 auxiliary inputs에 관한 부분입니다.

  • NRC에는 one-blob encoding을 적용하였고, NeRF에는 spherical harmonics basis를 적용하였습니다.

5. Experiments

5.1 Gigapixel Image Approximation

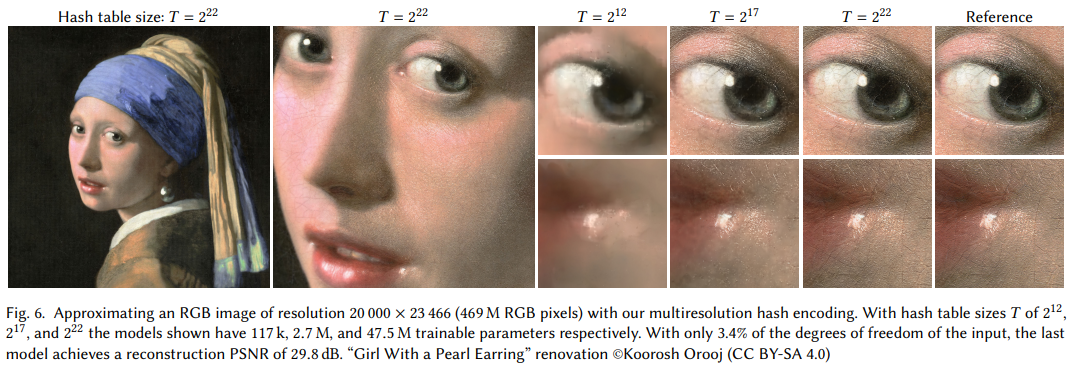
2D image 좌표를 RGB color로 매핑하여 모델이 high-frequency detail을 학습하는 task입니다. 논문 출판 당시 SOTA 모델인 ACORN과 같은 PSNR을 기록하였는데, 학습 시간은 2.5분입니다(!).

5.2 Signed Distance Functions

SDF는 3D shape를 물체 표면까지와의 거리로 매핑하는 task입니다. 논문 기준 SOTA인 NGLOD와 동일한 파라미터 수를 사용하였고, NGLOD보다 높은 quality를 기록하지는 못하였지만 IoU 관점에선 비슷한 quality를 보여주었습니다.

5.3 Neural Radiance Caching

Monte Carlo path tracer로부터 5D light field를 산출하는 task입니다. 논문 기준 SOTA인 Triangle Wave Encoding은 147FPS인 반면, hash encoding은 133FPS를 보여주었습니다. SOTA에 약간 못 미치는 성능입니다.

5.4 Neural Radiance and Density Fields (NeRF)

드디어 메인 task에 도달했습니다. NeRF는 spatial(3D) density function과 5D light field로 렌더링하는 task입니다.

Model Architecture

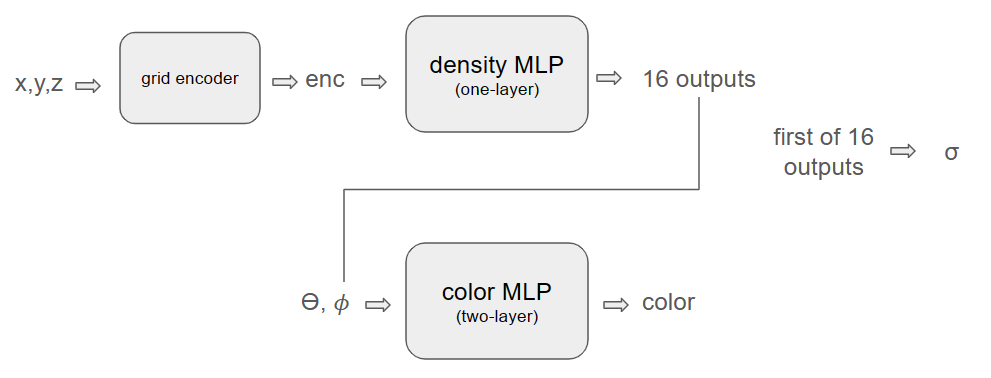
Instant NeRF는 density MLP와 color MLP로 구성됩니다. 논문에 기재된 것을 바탕으로 도식도를 간단히 그려보았습니다.

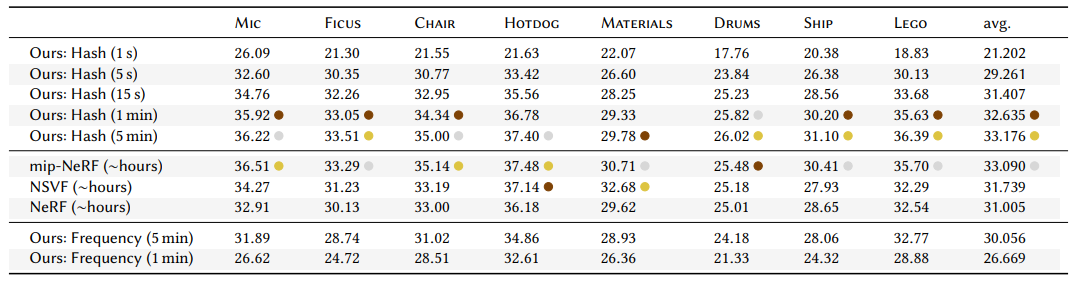
NeRF들과의 비교 테이블입니다. 대부분의 데이터셋에 대해 SOTA를 기록하였으며, Materials와 같은 복잡하고 view에 따른 반사가 이루어지는 scene에 대해서는 SOTA를 기록하지 못하였습니다.


Appendix

(논문 내 3. Multi-resolution hash encoding의 내용이 길어져 Appendix에서 따로 다루었습니다.)

Implicit hash collision resolution

coarse levels에서는 1:1 매칭이 이루어지므로 hash collision(다른 좌표 값이 같은 index를 갖는 현상)이 일어나지 않습니다. 하지만 scene의 low-resolution만 표현 가능합니다. 반면, fine levels에서는 scene의 작은 부분들도 잡아낼 수 있지만 많은 collision이 일어납니다.

그럼에도 hash collision에 대한 따로 처리를 하지 않았는데, 파라미터를 학습하는 과정에서 scene에서 더 중요한 sample이 collision average에 큰 영향을 주기 때문입니다. visible surface에 있는 point들이 주로 중요한 sample로 작용됩니다.

Online adaptivity

inputs x\mathbf{x}의 분포가 학습하면서 변화하면(x\mathbf{x}의 분포가 더 작은 지역에 집중하게 되면), finer grid levels이 더 적은 collision과 더 정확한 hash function을 얻게 됩니다. 즉, hash encoding이 자동적으로 data distribution을 학습하게 됩니다.

d-linear interpolation

grid는 불연속성을 가지기 때문에, encoding enc(x;θ)\text{enc}(\mathbf{x};\theta)과 neural net의 chain rule이 연속적이게 되려면 interpolation을 거쳐야 합니다.


Reference

[1] Instant Neural Graphics Primitives with a Multiresolution Hash Encoding, THOMAS MÜLLER, ALEX EVANS, CHRISTOPH SCHIED, ALEXANDER KELLER(NVIDIA), arxiv.org/pdf/2201.05989

[2] HashNeRF Github, GitHub - yashbhalgat/HashNeRF-pytorch: Pure PyTorch Implementation of NVIDIA paper on Instant Training of Neural Graphics primitives: https://nvlabs.github.io/instant-ngp/

profile
김민솔
Interested in Vision, Generative, NeRFs
이전 포스트

NeRF

다음 포스트

NeRF in the Wild

0개의 댓글