NeRF

김민솔·2023년 8월 21일

NeRF

목록 보기

1/10

NeRF

NeRF는 ECCV 2020 best paper에 선정되어 많은 주목을 받았고, 현재까지도 NeRF를 기반으로 발전시킨 논문들이 등장하고 있습니다. 따라서 해당 분야를 팔로업하기 위해서 Neural Radience Field를 최초로 제안한 논문을 분석해보았습니다. NeRF를 이해하기 위해선 Background가 많이 요구되는데, 아래에 Appendix 부분에서 설명하였으니 이를 참고하여 글을 읽으시면 더 도움이 될 것입니다.

NeRF는 특정 시점에서 얻은 이미지들을 통해서 해당 물체를 다양한 시점에서 바라보았을 때를 예측하여 결과적으로 2D 물체를 3D로 보이게 하는 모델입니다.

기존 연구와 달리 Deep Convolutional Layer가 아닌(Deep CNN을 사용하여 렌더링을 하였을 때는 많은 데이터셋을 요구하는 점, 시간이 매우 오래 걸리며 공간 복잡도가 큰 점 등 많은 문제점이 존재하였습니다.) MLP를 사용하여 Radience Field를 구성하였으며, 모델의 대략적인 구조는 다음과 같습니다. Network의 input으로 spatial loaction $(x,y,z)$ 와 viewing direction $(θ, φ)$ 로 이루어진 5D의 연속된 좌표 값을 구성하고, output은 volume density와 view에 따라 방출되는 radiance로 설정하였습니다. Camera rays를 따라 5D 좌표들을 생성하고, volume rendering을 통해 output colors(RGB)와 density를 얻어내어 객체를 렌더링합니다.

3. Neural Radiance Field Scene Representation

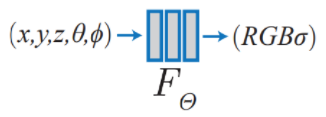
앞서 언급했던것 처럼 Camera ray 내의 3D location $(x, y, z)$ 과 2D viewing direction $(θ, φ)$ 로 구성된 5D vector를 모델의 input으로, color $(r, g, b)$ and volume density $σ$ 를 모델의 output으로 합니다. 이때 input으로 3D location을 설정하는 것은 당연하게 받아들일 수 있지만, viewing direction을 왜 두었는지 궁금해하실 수도 있을 것입니다.

viewing direction

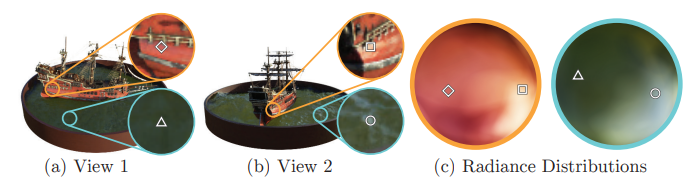
위의 그림에서 보는 것과 같이, 같은 3D point여도 시점에 따라서 RGB 값이 바뀌는 non-Lambertian 효과를 고려하여 viewing direction을 input으로 설정한 것입니다. 또한 viewing direction 없이 3D location으로만 학습해본 결과, 모델이 피사체의 specularities를 나타내지 못하였습니다.

MLP network (weights = Θ)

F_Θ : (x, d) → (c, σ)

volume density $σ$ 는 location 정보로만, color $(r, g, b)$ 는 location과 viewing direction을 같이 사용하여 output을 구했습니다.

MLP network structure

network structure

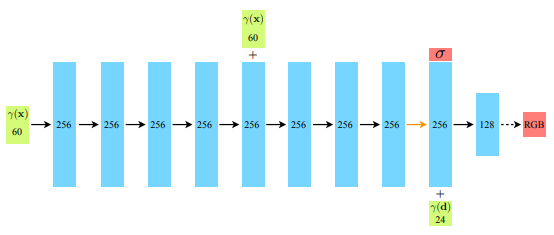
(1) 3D coordinate x는 8개의 dense layer(256 channels + ReLU)를 통과하도록 하였고 (2) 다음 레이어에서 volume density $σ$ 를 산출 및 256 차원의 feature vector를 viewing direction과 concat하였습니다. (3) 최종 layer(128 channels + ReLU)를 통과한 후에 view-dependent RGB color를 얻어내는 것으로 모델을 디자인했습니다.

5번째 layer에서 skip connection을 한 점과, 최종 레이어에서 activation으로 sigmoid를 사용한 것도 확인할 수 있습니다.

4. Volume Rendering with Radiance Fields

C(r) = \int^{t_f}_{t_n} T(t)σ(r(t))c(r(t), d)dt \ , \quad where \ T(t) = exp( - \int^{t}_{t_n} σ(r(s))ds) \ .

Camera ray $r(t) = o + td$
near and far bounds → $t_n$ and $t_f$
$T(t)$ 는 ray에서 t까지의 축적된 투과도를 나타내는 식입니다. ray에서 나타내고자 하는 픽셀 앞에 거대한 장애물이 존재한다면 해당 픽셀은 잘 보이지 않게 될 것입니다. 따라서 t 전까지의 밀도 합이 클수록 T(t)의 값이 작아지면서 C(r)의 값이 작아지게 됩니다.

$C(r)$ 은 t 시점까지의 축적된 투과도인 $T(t)$ , volume density $σ(r(t))$ , t시점에서의 color 값 $c(r(t), d)$ 을 모두 곱한 것들을 적분하여 ray가 가지는 RGB Color 값을 구하는 식입니다.

strarified sampling

t_i ∼ \mu [t_n + \frac {i − 1} N (t_f − t_n), \ t_n + \frac i N(t_f − t_n)]

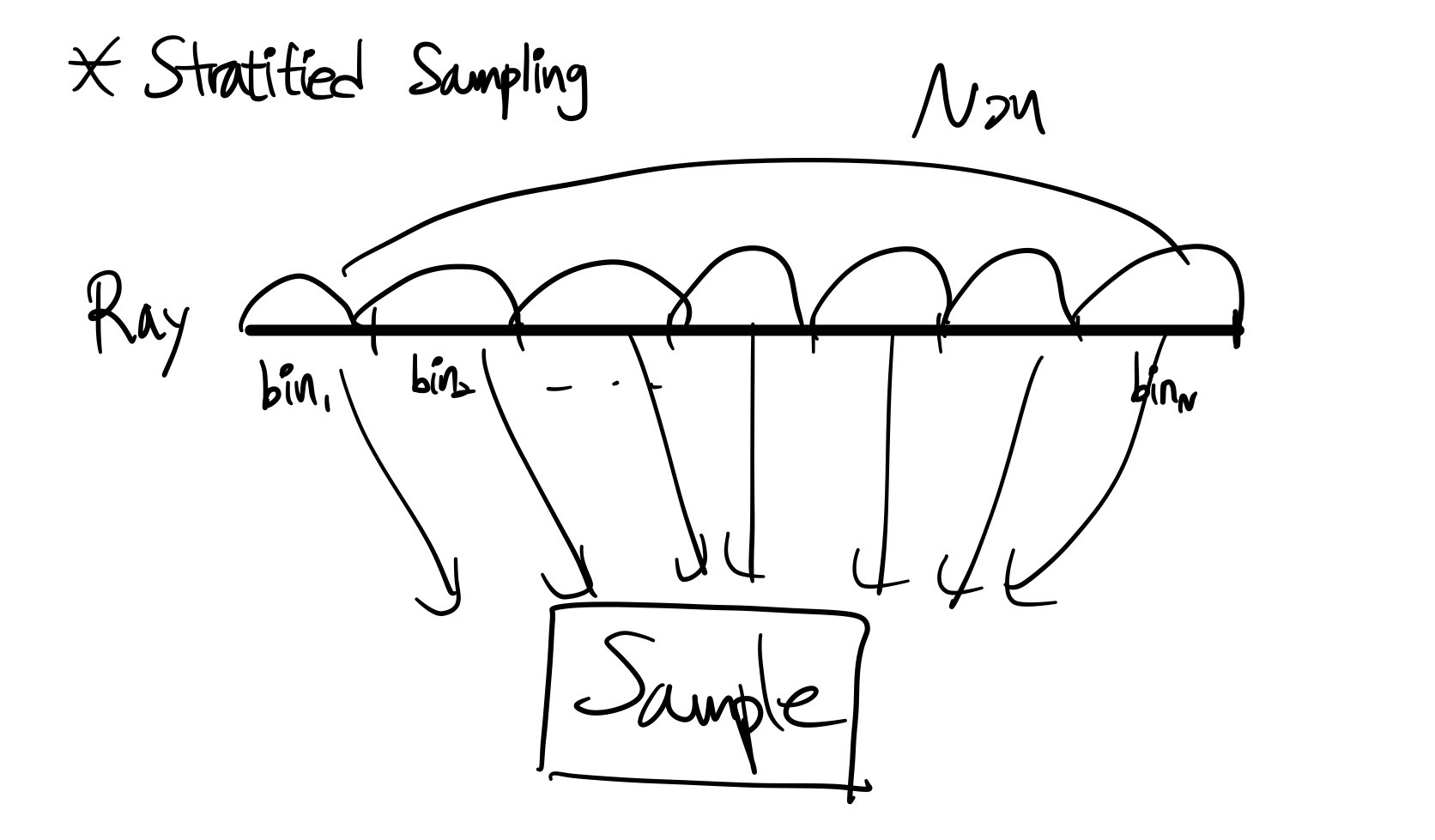
일반적인 렌더링 기법인 quadrature(구분구적법)을 사용한다면, 불연속적인 voxel grids가 고정된 지역의 집합에서만 쿼리되는 현상이 발생하고 이는 이미지의 해상도를 제한하는 효과를 줍니다. 따라서 stratified sampling을 사용하였는데, 이는 ray를 N개의 bin으로 나누고 각 bin에서 균일하게 샘플을 추출하는 방식입니다. stratified sampling을 통해 ray의 전체적인 부분에서 샘플들을 얻어낼 수 있습니다.

최종 렌더링 함수

\hat{C}(r) = \sum^N_{i=1} T_i(1 - exp(−σ_iδ_i))c_i \ , \quad where \ T_i = exp(-\sum^{i-1}_{j=1} −σ_iδ_i)

$δ_i = t_{i+1} − t_i$ : 인접한 샘플들과의 거리
$α_i = 1 − exp(−σ_iδ_i)$ : volume density

최종적으로 Color 값을 산출하는 식은 다음과 같습니다. 위의 식을 기존 논문에서 랜더링에 사용하는 방식을 차용하여 바꾼 것이며, integral을 weighted sum의 방식으로 표현한 것입니다.

5. Optimizing a Neural Radiance Field

Positional encoding

Neural network를 사용하여 함수의 근사값을 표현하는 것은 보편적인 방법이지만, network에 $xyzθφ$ 를 단순 input으로 주는 것은 이미지의 high-frequency가 사라지는 결과를 보였습니다.

Positional encoding을 통해서 input 자체에서 high-frequency를 가질 수 있도록 하였습니다.

γ(p) = (sin(2^0πp), cos(2^0πp), · · · , sin(2^{L−1}πp), cos(2^{L−1}πp)

실험 결과를 통해, coordinates인 (x,y,z)에는 L = 10 / viewing direction unit vector d에는 L = 4를 적용하였습니다.

cf)
Transformer에서도 ‘positional encoding’을 사용하는데, 이는 불연속적인 토큰들을 하나의 시퀀스로 표현할 때에 사용합니다. 반면 NeRF에선, input의 차원을 높이기 위해 사용된 것이므로 동음이의어라고 보는 것이 좋을 것 같습니다.

Hierarchical volume sampling

\hat{C}_c(r) = \sum ^{N_c}_{i=1}w_ic_i , \quad wi = Ti(1 − exp(−σiδi)).

앞서 언급한 렌더링 방식(ray의 N query points에서 neural radiance field net을 평가하는 것)이 비효율적이라는 점을 제시하였습니다. 빈 공간 혹은 가려진 공간과 같은 렌더링에 도움이 되지 않는 지역들도 반복되어 샘플링되기 때문입니다.

저자들은 이를 두 개의 네트워크를 최적화시키는 방법으로 해결하고자 하였습니다. → coarse network / fine network

coarse network는 위에서 언급한 volume sampling 방법을 동일하게 적용합니다.

Coarse network에서 구한 weights들을 normalizing( $\hat{w_i} = w_i /\ sum^{N_c}_{j=1} w_j$ )하여 piecewise-constant PDF로 생성한 후 inverse transform sampling을 통해 위의 PDF에서 두 번째 샘플들을 추출합니다. 한 번 샘플링을 거친 weights에서 inverse transform sampling을 하게 되면 weights가 큰 부분에서 더 많은 샘플들을 추출하게 되는데, 밀도가 높은 부분이 물체의 핵심 부분일 확률이 높으므로 더 가중치를 두어 샘플을 뽑는 것으로 이해할 수 있습니다.

fine network에선 coarse network에서 사용한 샘플인 $N_c$ 와 두 번째 샘플인 $N_f$ 를 모두 사용하여 $\hat{C}_f$ 를 계산하였습니다.

6. Results

results

Diffuse Synthetic 360◦, Realistic Synthetic 360◦, Real Forward-Facing 총 3개의 데이터셋에 대해 PSNR, SSIM, LPIPS 3개의 평가지표를 측정하였고, 각 데이터셋에 대해 기존 연구들보다 우수한 평가 지표를 보여주었습니다. Real Forward-Facing에서 LPIPS 지표가 LLFF보다 약간 떨어지는데, 이에 대한 분석은 논문에 잘 기재되어 있으니 알고 싶으신 분들은 찾아보시면 좋을 것 같습니다.

평가지표1
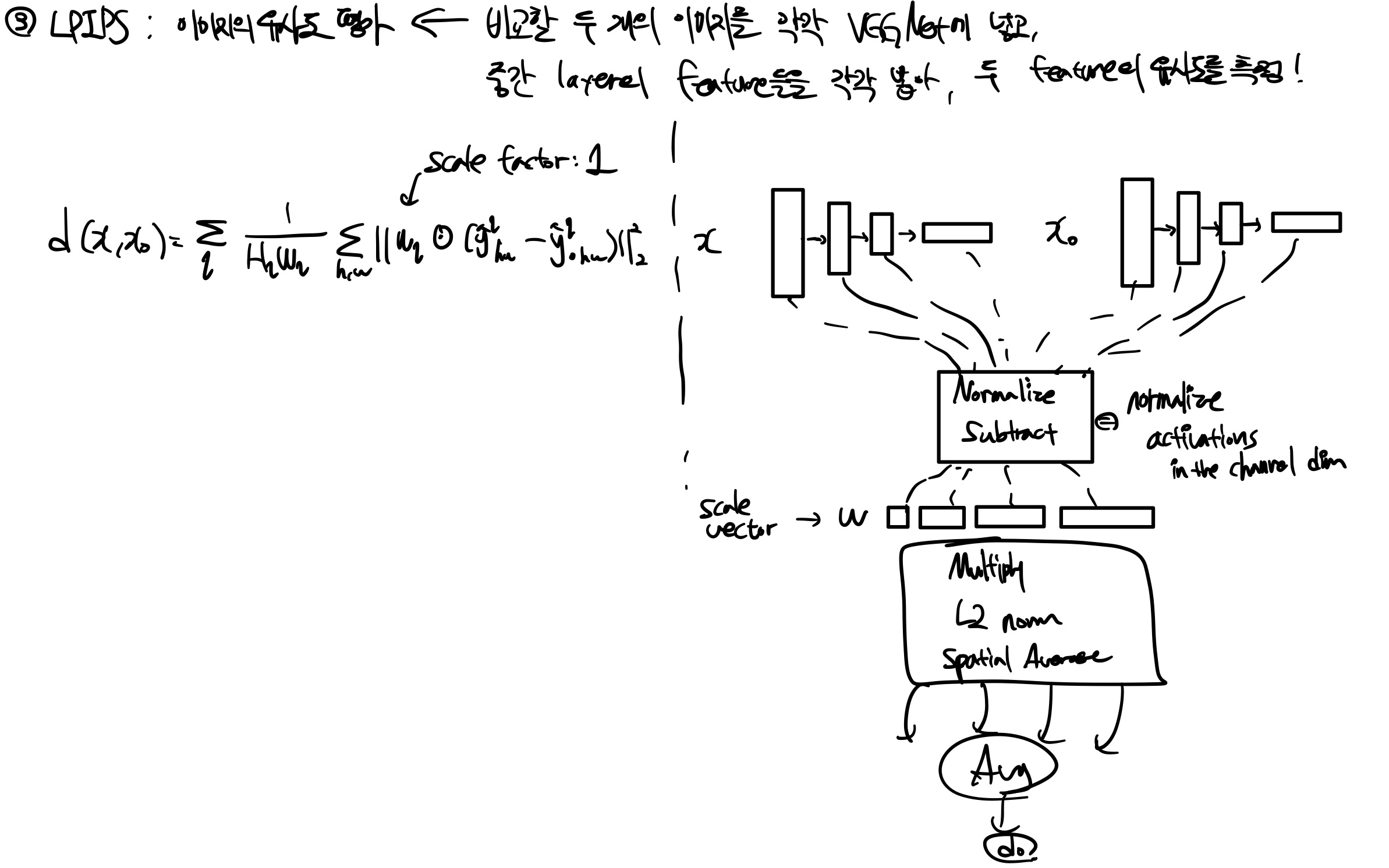
평가지표2

Appendix

Camera 좌표계

NeRF에선 전반적으로 카메라에 관한 개념들이 중요하게 사용됩니다. NeRF를 이해하기 위해 필요한 개념들을 정리해보았습니다.

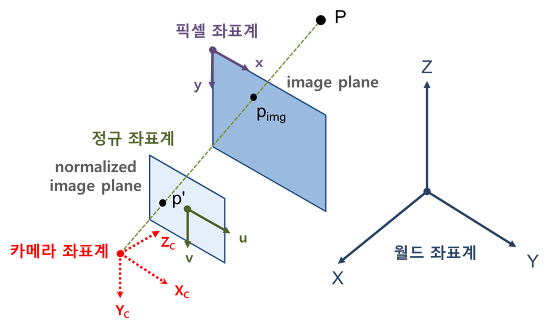
카메라가 실제(월드 좌표계)로 존재하는 물체를 담아낼 때에는 다음과 같은 4가지의 좌표계가 사용됩니다.

1) 월드 좌표계

실제 세상에서 피사체가 존재하는 위치를 나타내는 좌표계입니다. 월드 좌표계가 물체의 위치를 표현할 때 좌표계들의 기준이 되며 X, Y, Z 축은 임의로 설정 가능합니다.

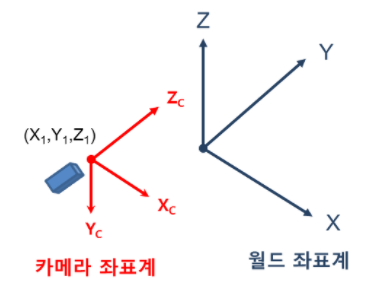
2) 카메라 좌표계

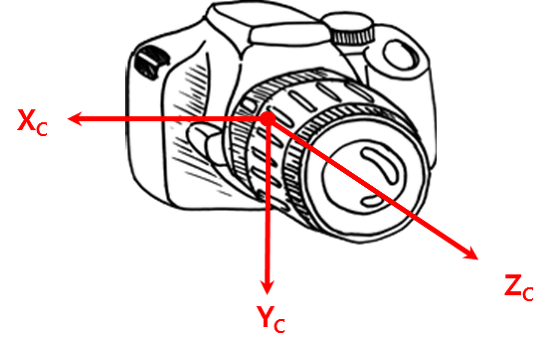
카메라 좌표계는 카메라를 기준으로 위치를 표현하는 좌표계입니다. 카메라 렌즈의 중심을 원점으로 잡으며, 카메라 정면 광학축 방향을 z축. 아래 방향을 y축, 카메라 오른쪽 방향을 x축으로 설정합니다. 이때 아래에서 설명할 Camera ray의 방향이 z축과 일치하게 됩니다.

3) 이미지 좌표계(픽셀 좌표계)

이미지 좌표계는 이미지에서 픽셀을 표현하는 좌표계입니다. 이미지의 좌측 상단 모서리를 원점으로 두고, 오른쪽 방향을 x축 증가 방향으로, 아래쪽 방향을 y축 증가 방향으로 설정합니다.

카메라의 기하학적 의미는 Real World Coordinate(월드 좌표계)를 Image coordinate(이미지 좌표계)로 나타내는 것입니다. 따라서 (X, Y, Z)를 이미지 좌표계의 (x, y)로 projection하는 것이 카메라의 주 목적이 됩니다.

반면 NeRF에서는 이미지 좌표계를 월드 좌표계로 나타내는 것이 주 목적이 됩니다. 이어서 설명할 instrinsic과 extrinsic을 역으로 이용하는 것이 NeRF에서 사용됩니다.

4) 정규 좌표계

정규 좌표계는 실제로 존재하진 않지만, 월드 좌표계를 이미지 좌표계로 나타내기 위하여 도입된 좌표계입니다. 어떠한 장면을 촬영할 때, 동일한 장면과 방향에서 이미지를 찍었더라도 카메라 종류 혹은 세팅에 따라 다른 이미지를 얻게 됩니다. 카메라 간의 차이는 기하학적으로 불필요한 요소이기 때문에 정규 좌표계를 두어 Camera intrinsic의 영향을 제거한 것입니다.

정규 좌표계를 의미적으로 접근하면, 카메라 초점 거리가 1인 이미지 평면을 나타낸 좌표계입니다. 좌표는 (u, v, 1)로 나타내며 좌표계의 원점이 이미지의 중심이라는 것이 이미지 좌표계와 큰 차이점입니다.
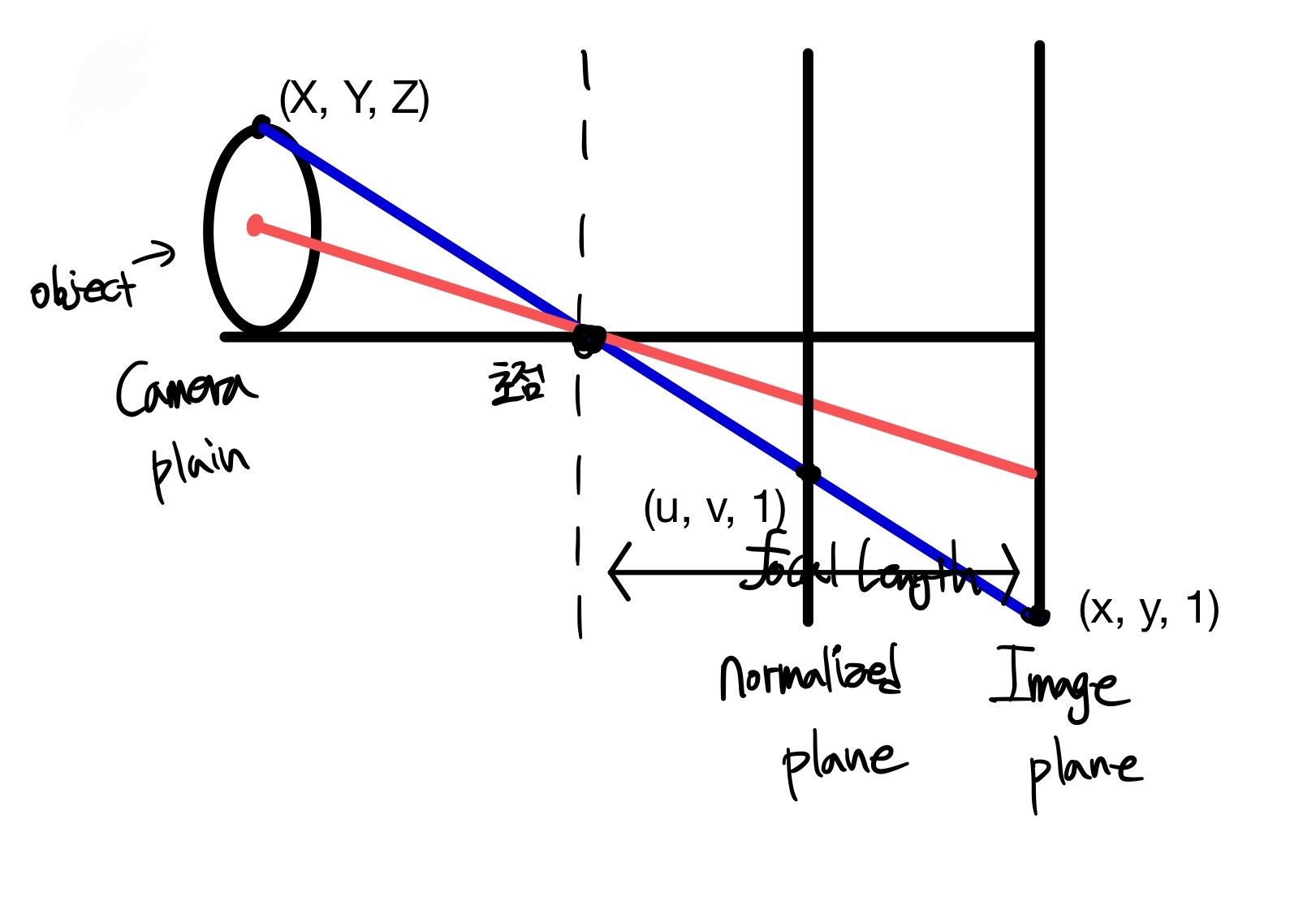
coords

Camera intrinsic

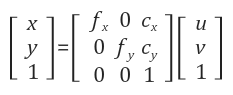
f: focal length(초점 거리)
c: principal point(광학축(z축)과 이미지 평면이 만나는 픽셀 좌표)

Camera intrinsic은 카메라 내부 파라미터로 이미지 좌표계를 정규 좌표계로 변환하는 역할을 합니다.

x = f_xu + c_x \\ y = f_yv + c_y

정규 좌표계에서 이미지 좌표계로 역변환 시에는 다음의 공식을 활용합니다.

u = (x-c_x) / f_x \\ v = (y-c_y) / f_y

Camera extrinsic

Real Coordinates를 Camera Coordinates로 변환하기 위해서 사용합니다.

회전 변환

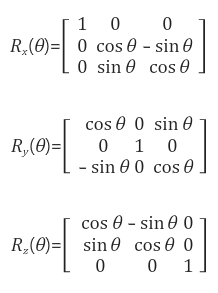
좌표계를 변환하기 위해선 우선 회전 변환에 대해 알아야 합니다. 선형대수학에서 배웠던 것과 같은 3D 회전 변환을 사용합니다.

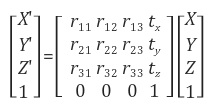
회전 변환인 R로 좌표축을 변환한 후에, 평행이동 T를 변환에 사용하여 최종적으로 월드 좌표계를 카메라 좌표계로 변환합니다.

NeRF에서는 Camera 좌표계 → Real World 좌표계로 변환해야 합니다.

C2W가 이루어지는 과정을 아래와 같이 표현해보았습니다

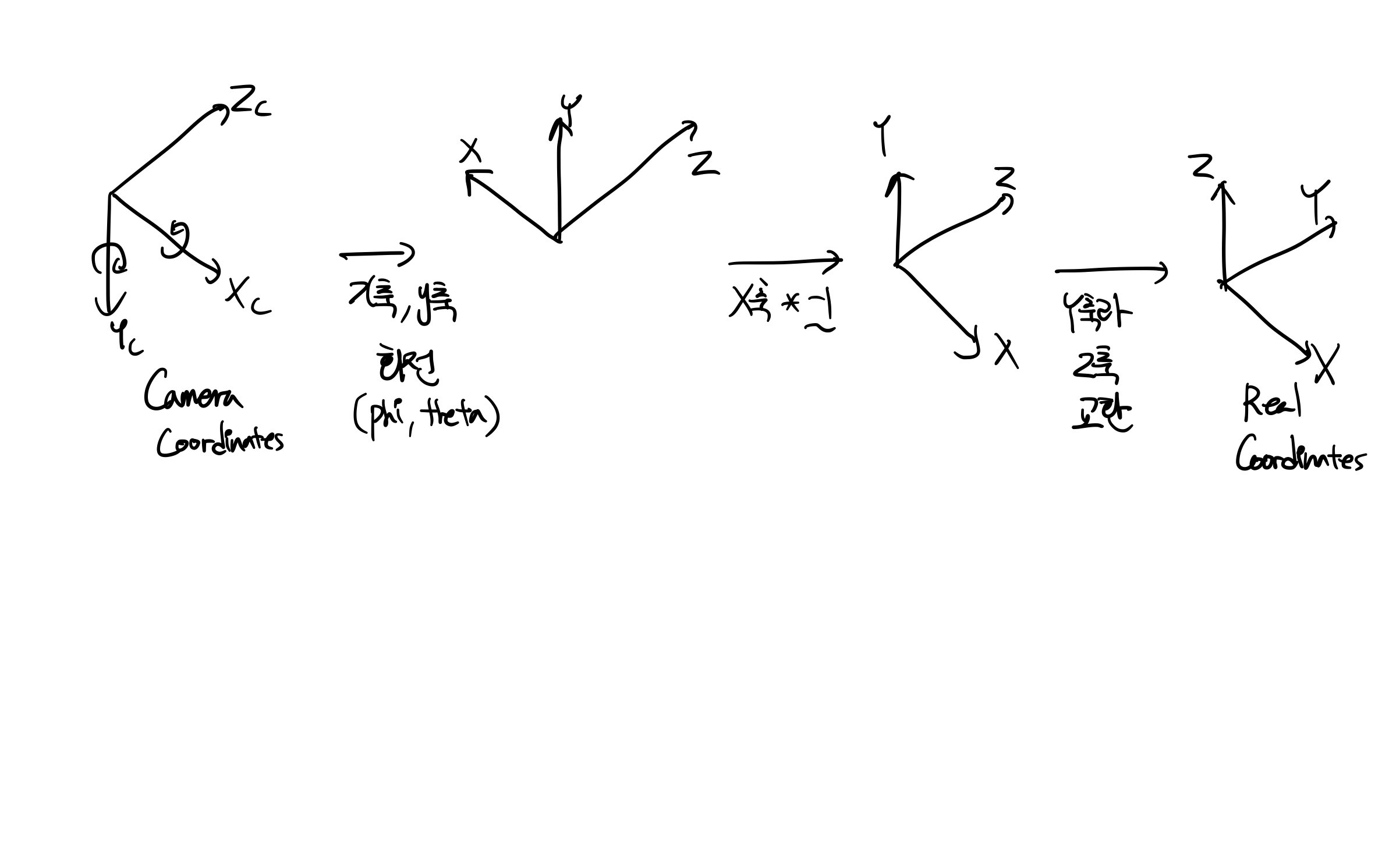
Camera ray / Volume ray casting

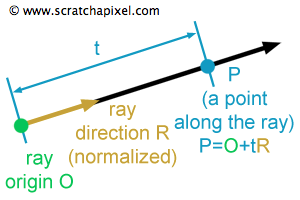
말 그대로 카메라에서 보내는 광선입니다. 시작점(Origin)과 방향(Direction)이 주어지면, 시작점에서 해당 방향으로 쭉 선을 그으면 이것이 ray가 됩니다.

Volume ray casting은 요약하자면 ray를 쏘아 물체 표면에 맞았을 때, 이를 뚫고 지나간 후에 ray를 따라 샘플링하는 것을 의미합니다. Volume ray casting이 이루어지는 방법은 다음과 같습니다.

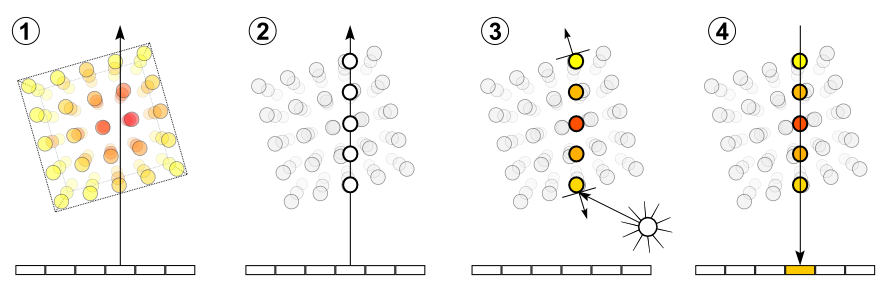
① Ray casting

이미지의 각 픽셀에 대해 볼륨을 투과하여 ray를 쏩니다.

② Sampling

볼륨을 투과한 ray를 따라서 샘플을 추출합니다. 이때, 볼륨이 ray와 정렬되어 있지 않을 뿐만 아니라 주로 샘플링 포인트가 voxel 사이에 위치한다는 점을 주의해야 합니다. 따라서 voxel을 기준으로 샘플링 값을 interpolation하는 과정을 거치게 됩니다.

③ Shading

각 샘플링 포인트들에 대해 transfer function을 적용하여 RGBA material colour and a gradient of illumination values를 얻습니다. 이때의 gradient는 볼륨 내의 표면적의 방향을 의미합니다.(일반적인 경도에 대한 설명)

④ Composition

ray 위에 놓인 Shading된 샘플링 포인트들의 RGBA 값과 gradient를 조합하여 pixel의 최종 color 값을 구합니다.

이러한 Volume ray casting을 통해서 원하는 픽셀의 최종적인 color 값을 얻어낼 수 있습니다.

Inverse transform sampling

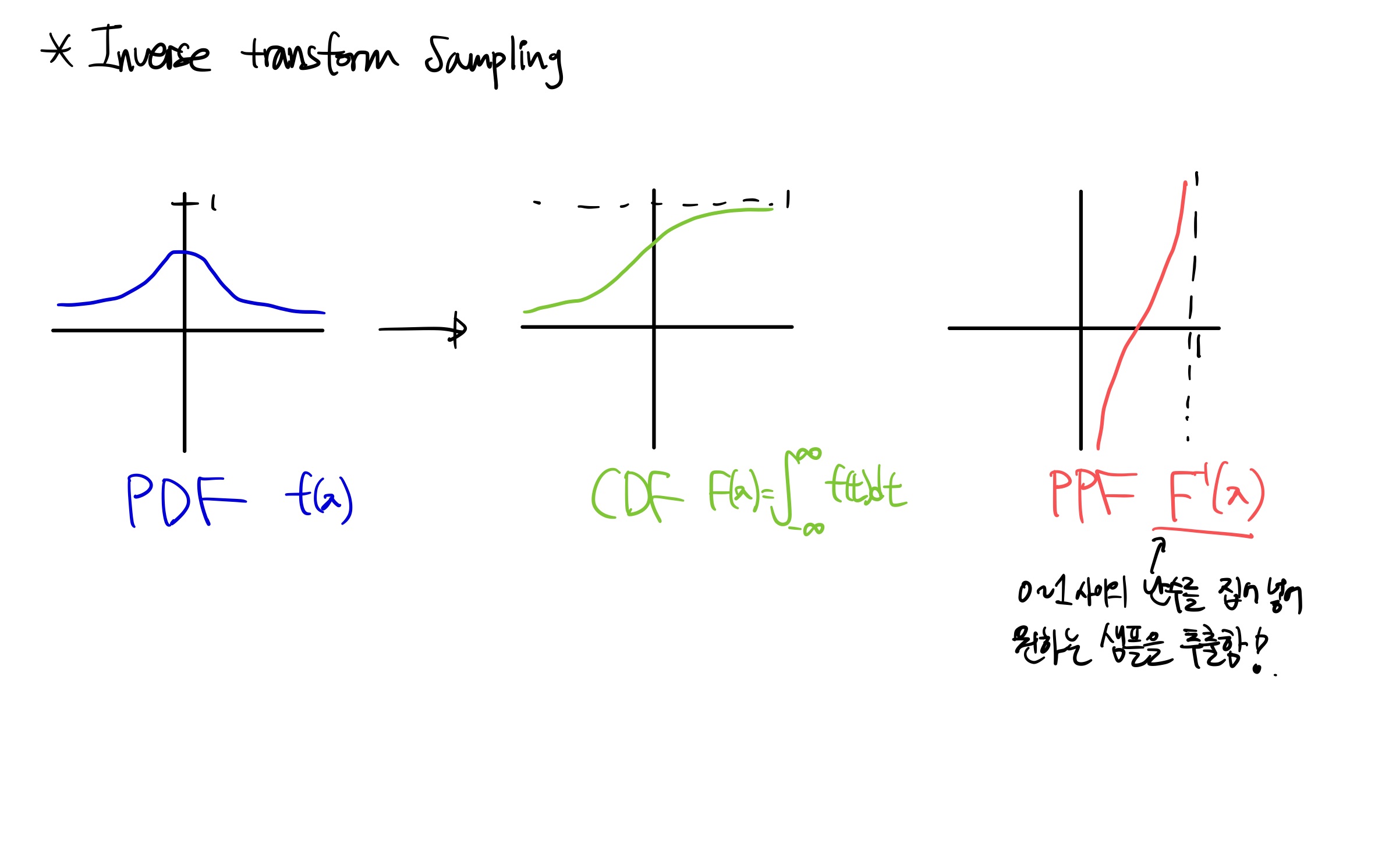
Inverse transform sampling은 PDF에서 샘플을 추출하는 대표적인 방법 중 하나입니다. PDF(probabilty distribution function)의 CDF(cumulative distirbution function)를 구한 후 역함수를 취하여 0~1 사이의 난수를 역함수에 집어넣어 샘플을 추출하는 방법입니다.