VQ-VAE

VQ-VAE(Vector Quantised-Variational AutoEncoder)가 VAE와 다른 점은 두 가지입니다. (1) 인코더 네트워크가 불연속적인 latent space를 생성하고, (2) prior가 고정되지 않고 학습됩니다.

불연속적인 latent space를 표현하기 위해 vector quantisation을 도입하였으며 이를 통해 VAE에서 발생하는 “posterior collapse” 문제를 해결하였습니다. posterior collapse란, latent vector가 autoregressive decoder에 의해 무시되는 현상입니다.

또한 VQ-VAE는 autoregressive prior를 통해 latent representation을 구현하면서 이전(Vanila VAE)보다 높은 퀄리티의 이미지와 비디오, 오디오를 생성할 수 있었습니다.

VQ-VAE

VQ-VAE를 알아보기 전, VAE에 대해 간단하게 알아보겠습니다.

참고: CS231n 2017 Lecture 13. [2]

• $q(z|x$) : Encoder → parameterises posterior distribution
• $z$ : discrete latent random variables
• $x$ : input data
• $p(z)$ : prior distribution
• $p(x|z)$ : Decoder → parameterises posterior distribution
  
  
  
  

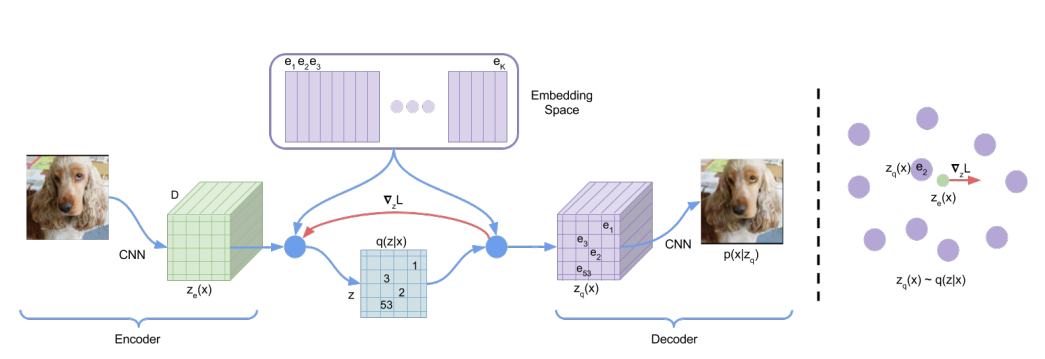
Discrete Latent variables

저자들은 latent embedding space를 $e \in R^{K \times D}$ 로 정의합니다.

• $K$ : latent space의 크기
• $D$ : 각 latent vector의 차원

모델이 input $x$를 받아 인코더를 거쳐 $z_e(x)$를 출력합니다. discrete latent varibles $z$는 임베딩 공간을 nearest neighbor look-up하여 계산됩니다. decoder의 input으로는 상응하는 임베딩 벡터가 들어옵니다.

이러한 forward 과정은 오토인코더와 유사하지만 discrete embedding space를 구성하여 비선형성을 띈다는 점이 중요합니다.

Posterior categorical function인 $q(z|x)$은 원핫 벡터로 표현되며 정의는 다음과 같습니다.

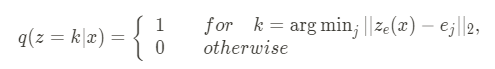
Proposal distribution $q(z = k|x)$는 결정론적입니다. 즉, 입력값에 관계 없이 일정한 결괏값을 내놓기 때문에 해당 식으로 표현됩니다.

인코더의 output인 $z_e(x)$는 embedding $e$의 nearest neighbor로 매핑되며, 식은 다음과 같습니다.

하지만 해당 식에서 실제 gradient는 존재하지 않습니다. 하지만 디코더에서의 gradient와 근사치를 갖는다고 두어 디코더의 input $z_q(x)$를 복사해서 인코더의 output인 $z_e(x)$에 사용합니다.

Forward 시에는 nearest embedding z_q(x)가 디코더에 전달되고, Backward 시 $\bigtriangledown_zL$ 이 그대로 인코더에 전달됩니다. 인코더의 출력과 디코더의 입력이 같은 차원을 공유하면서 gradients가 reconstructure loss를 줄이기 위해 인코더를 어떻게 변화시켜야 하는지에 관한 정보를 담게 됩니다.

Learning

전체적인 loss 함수는 세 가지의 구성 요소들로 이루어져 있습니다.

(1) reconstruction loss: $\log p(x|z_q(x))$

recon loss는 VAE에서도 언급되는, 디코더와 인코더 최적화에 사용되는 loss 식입니다.

디코더로 생성된 ouptut과 origin 사이의 MLE로 계산됩니다.




(2) VQ loss: $||sg[z_e(x)] - e ||^2_2$

앞서 언급했듯이, gradient는 복사되어 인코더에서 디코더로 전달되기 때문에 임베딩은 recon loss로 gradient update가 되지 않습니다. 따라서 임베딩 공간을 학습하기 위하여 간단한 dictionary 학습 알고리즘은 Vector Quantisation(VQ)를 사용하였습니다. VQ loss는 L2 loss로 임베딩 벡터 $e_i$를 인코더의 output $z_e(x)$으로 이동시킵니다.




(3) commitment loss: $\beta ||z_e(x) - sg [e]||^2_2$

임베딩 공간의 차원이 정해지지 않았기 때문에, 인코더 파라미터만큼 빠르게 학습되지 않을 경우 임베딩 공간의 volume이 임의로 커지는 상황이 발생합니다. 인코더의 임베딩 생성에 집중하고, output이 커지지 않도록 하기 위해 commitment loss를 두었습니다.

VQ와 commit loss에서 사용된 sg는 stopgradient operator를 의미하며 forward 시 연산을 제약시켜 update되지 않는 상수를 만드는 identity입니다.

• ELBO

저자들은 $\log p(x)$를 ELBO 문제로 바라볼 수 있기 때문에 VQ-VAE가 VAE의 종류로 볼 수 있다고 주장합니다. 또한 $z$를 단순한 uniform prior로 두었기 때문에 KL Divergence 값도 $\log K$인 상수가 되어 ELBO 식에서 흡수됩니다.

Prior

불연속적인 latents $p(z)$의 prior distribution은 categorical distribution입니다. 그리고 feature map 내의 다른 $z$를 통해서 autoregressive 상태로 될 수 있습니다. VQ-VAE를 훈련하는 동안에는 prior가 불변할 뿐만 아니라 균일하집니다. 따라서 훈련이 끝난 뒤 autoregressive distribution을 추가로 학습시킵니다. 이를 통해 ancestral sampling으로 $x$를 만들어낼 수 있게 됩니다.

Reference

[1] Google DeepMind (2017), “Neural Discrete Representation Learning”, https://arxiv.org/pdf/2010.11929.pdf

[2] Stanford Univ. (2017), Lecture 13. “Generative models” in CS231n, https://www.youtube.com/watch?v=5WoItGTWV54&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=13&t=2799s&pp=iAQB

---

VQ-VAE보다 훨씬 좋은 성능의 생성 모델들이 많기 때문에 Experiments는 생략하겠습니다..!




+작성자의 혼잣말

블로그를 꾸준하게 작성하고 싶은데, 군대에서 논문을 공부하는 것이 생각보다 쉽지는 않네요… 하지만 힘이 닿는 데까지 열심히 작성해보려고 합니다 ㅎㅎ. 아마 블로그 작성 내용들은 지금과 같은 논문 리뷰(1)와 논문 구현 코드 분석(2), 기타 교재나 강의 학습(3)이 될 것 같고 기타 좋은 내용이 있으면 공유해보겠습니다. 공부하고 싶은 내용들이 너무 많네요 차근차근 올려볼테니 기대해주세요!