Common Diffusion Noise Schedules and Sample Steps are Flawed 논문 리뷰

0. Abstract

• 저자들은 일반적인 Diffusion noise schedule은 last timestep에서 SNR이 0이 되도록 강제하지 않고, inference 시에 last timestep 에서 시작하지 않는다는 것을 발견했다. 이러한 결함있는 디자인은 inference와 train 시에 align이 되지않아 문제가 생긴다.
• Stable diffusion에서 모델은 중간 밝기의 이미지만 생성하도록 제약한다.
• 저자들은 이 논문에서 4가지의 방법을 제시한다.
  1. zero terminal SNR을 강제하기 위해 schedule을 rescale.
  2. v predtion을 통한 model train
  3. sampler를 항상 last timestep 에서부터 샘플링하도록 한다.
  4. classifier-free guidance를 rescale하여 over-exposure현상을 막는다.

이러한 간단한 변화로 inference와 train을 align 시키고, 모델이 더 원래 데이터 분포에 맞는 생성을 할 수 있게 한다고 주장한다.

1. Introduction

• 디퓨전은 최근들어 매우 좋은 성능을 내고 있지만, 중간 밝기의 이미지만 생성하고 있음. 예를 들어 “Solid background”, “A white background”를 생성하라고 하면 잘 생성하지 못함.

• 저자들은 이 문제가 noise schedule과 sampling 과정에서 생긴다는 것을 발견. 일반적인 scheuler는 signal-to-noise (SNR)을 zero로 만들도록 last timstep을 강제하지 않는다. → 예를 들어 1000step을 forward해도 정보가 남아있음. 따라서 학습시 마지막 timestep에서 정보가 모두 지워지지 않음.

• 따라서 lowest frequency information(long-wavelength) 들이 학습할 때 남아있게 된다. → 완전한 noise로부터 시작하지 않음. 하지만 inference 시에는 pure한 noise (평균 0, 가우시안 1)로부터 시작한다. 이는 모델이 중간 밝기의 이미지를 생성하도록 제약한다. 최신 샘플러들은 모든 timesteps를 거치며 샘플링 하지 않음(non-markovian). DDIM, PNDM과 같은 경우 샘플링 프로세스가 마지막 타임스텝에서 시작하지 않아 더욱 심한 문제가 발생.

• 저자들은 signal-to-noise (SNR)가 마지막 timestep에서 0이어야 하며, 샘플러는 diffusion training과 inference 과정을 align 시키기 위해 정확히 last timestep(T)에서 시작해야 한다고 주장함.

• 저자들은 zero terminal SNR을 만족시키도록 기존 schedule을 재조정하는 간단한 방법을 제안하고, SNR이 0으로 갈때 image의 (over-exposure)를 해결하기 위해 classifier-free guidance rescaling 테크닉을 제안한다.

2. Background

• Diffusion Model은 forward, backward를 포함.

forward

• joint : $q\left(x_{1: T} \mid x_0\right):=\prod_{t=1}^T q\left(x_t \mid x_{t-1}\right)$
• forward : $q\left(x_t \mid x_{t-1}\right):=\mathcal{N}\left(x_t ; \sqrt{1-\beta_t} x_{t-1}, \beta_t \mathbf{I}\right)$
• $q\left(x_t \mid x_0\right):=\mathcal{N}\left(x_t ; \sqrt{\bar{\alpha}_t} x_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right)$
• 다음과 같이 표현 가능. $x_t:=\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} \epsilon, \quad \text { where } \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ -> 식(4)
• SNR은 다음과 같이 표현. $\operatorname{SNR}(t):=\frac{\bar{\alpha}_t}{1-\bar{\alpha}_t}$ → SNR이 0으로 갈수록 noise

reverse

• $p_\theta\left(x_{0: T}\right):=p\left(x_T\right) \prod_{t=1}^T p_\theta\left(x_{t-1} \mid x_t\right)$
• $p_\theta\left(x_{t-1} \mid x_t\right):=\mathcal{N}\left(x_{t-1} ; \tilde{\mu}_t, \tilde{\beta}_t \mathbf{I}\right)$
• 평균값은 다시 노이즈로 매개변수화 한다. $\tilde{\mu}_t:=\frac{1}{\sqrt{\alpha_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon\right)$
• 분산은 다음과 같이 계산된다. $\tilde{\beta}t:=\frac{1-\bar{\alpha}{t-1}}{1-\bar{\alpha}_t} \beta_t$

3. Method

3.1. Enforce Zero Terminal SNR

Table 1.

• Table 1은 일반적인 schedule에서 SNR(T)와 $\sqrt{\bar{\alpha}_T}$를 보여준다. (T=1000)
  • cosine-schedule은 SNR이 0으로 가는것을 방지하기 위해 의도적으로 ${\beta}_t$를 0.999까지만 사용한다.
• Table을 보면 어떠한 schedule도 SNR(T)가 0이 아니다. 특히 Stable Diffusion에서 특히 SNR(T)가 0과 차이가 가장 크다. 이 값을 식 (4)에 넣어보면 완전한 noise가 아니라는 것을 알 수 있다. 이렇게 되면 학습 과정에서 t=T일 때 완전한 noise가 아닌 lowest frequency information(예를 들면 각 채널 별 평균 등)이 남아 있는 상태로 학습이 진행.
• inference 시에는 pure 한 가우시안 noise로부터 시작. 가우시안 noise는 평균이 0이므로 t=T에서 주어진 평균에 따라 샘플링을 진행하여, 모델은 결론적으로 평균 밝기의 이미지를 생성하게 된다.
  • {평균이 0인 이미지에서 mean이 0이고 분산이 1인 noise를 계속 제거하기 때문에 평균적으로 중간 밝기인 이미지를 생성하게 될것.} (필자의 생각)
  • {즉 학습 과정에서 내가 학습 시키고자 하는 어두운 이미지가 pure noise로 가서 거기서 부터 어두운 이미지로 오는 방법을 학습해야하는데, 학습에서 그렇게 pure noise로부터 어두운 이미지로 오는방법을 알지 못하게 됌(forward 시 SNR이 zero가 아니기 때문에 pure한 noise로 가지 않음). inference시에는 pure한 noise로부터 시작하기 때문에 평균적인 이미지를 생성하게 되는 것임.} (필자의 생각)
• SNR이 0으로 가는 schedule은 train 시에도 t=T에서 pure noise를 사용하므로 inferece와 동일한 조건이다.
  • 따라서, 저자들은 SNR이 완전한 0으로 가게(zero terminal SNR) 만드는 schedule을 사용해야하고, VE formulation은 SNR이 0으로 갈 수 없기 때문에 VP formulation을 사용해야 한다고 주장.
• 저자들은 SNR을 0으로 가게 하기 위해 VP formulation에 따라 noise schedule을 rescaling 한다. $\sqrt{\bar{\alpha}_t}$는 혼합될 잡음의 양을 결정하는것을 기억하자. 일단 $\sqrt{\bar{\alpha}_1}$을 그대로 두고, $\sqrt{\bar{\alpha}_T}$를 zero로 두고서 $\sqrt{\bar{\alpha}_t}$를 linearly하게 rescaling 하는 것. (t ∈ [2, . . . , T −1] )
• $\sqrt{\bar{\alpha}_t}$ 를 변경 시키는 것이 SNR(t)를 변경 시키는 거 보다 곡선을 더 잘 보존하는 것을 발견. → 구현은 알고리즘 1. 에 있음
• 이 방법은 non-cosine schedule에만 적용 가능. cosine의 경우에는 ${\beta}_t$ clipping을 하지 않고 zero terminal SNR을 달성 가능. 이때 ${\beta}_T$를 1로 보장해야함.

결과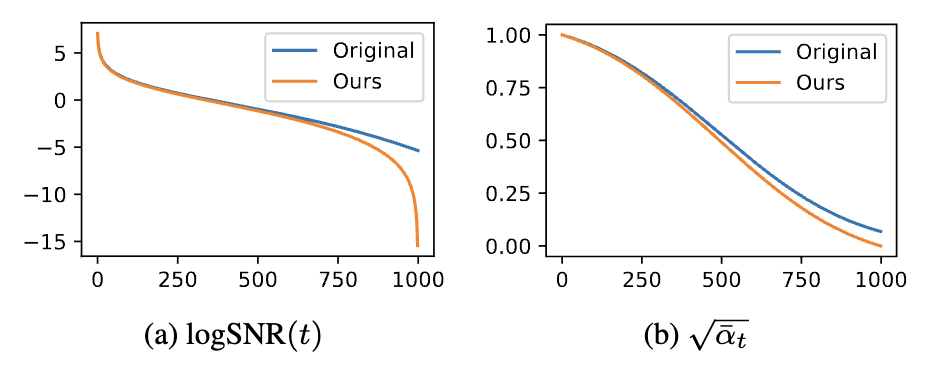

• SD의 schedule과 여기서 제안한 방법으로 rescaling 한 schedule의 SNR

알고리즘 1.

3.2. Train with V Prediction and V Loss → 아직은 완벽히 이해 X

• SNR이 0이되면 ${\epsilon}$ 예측은 사소한 task가 되고 ${\epsilon}$ loss는 데이터로부터 유의미한 것을 배울 수 없다.

• Tim Salimans and Jonathan Ho. Progressive distillation for fast sampling of diffusion models, 2022 에서 제안된 대로 모델 학습을 v prediction과 v loss로 변경.

• $x_t:=\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} \epsilon$

• $v_t=\sqrt{\bar{\alpha}_t} \epsilon-\sqrt{1-\bar{\alpha}_t} x_0$

• $\mathcal{L}=\lambda_t\left\|v_t-\tilde{v}_t\right\|_2^2$

• zero terminal SNR이 되도록 schedule을 rescaling 한 후에 t=T, $\sqrt{\bar{\alpha}_T}$=0 에서 $v_T = x_0$ 이다. 이제 모델은 pure한 noise $\epsilon$ 을 input으로 $x_0$를 예측하게 된다. t=T에서는 이제 어떠한 signal도 가지고 있지 않기 때문에 denosing을 수행하지 않고, prompt를 통해서 data distribution의 mean을 예측하는 역할을 하게 된다.

• SD에서 $\lambda_t$가 1일때 v loss를 사용하는 것이 $\epsilon$ loss를 사용하는 것과 유사한 퀄리티를 가지는 것을 발견했다. 저자들은 항상 v loss를 사용하고 $\lambda_t$를 조정하는 것이 좋다고 말한다.

3.3. Sample from the Last Timestep

• 최신 샘플러들은 적은 step으로만 샘플을 생성. 일반적으로 학습시에는 이산화된 timestep T=1000까지 사용하고 inference 시에는 S=25정도의 step으로 생성함.
• DDIM, PNDM과 같은 경우 샘플링 프로세스는 마지막 타임스텝을 포함하지 않음. 이 것은 3.1 Section에서 설명한 것과 같이 밝기에 대해서 악영향을 미친다.
• 저자들은 학습시 zero terminal SNR을 만족시키는 schedule과 함께 inference 시에 T=last timestep에서 시작하는 것이 중요하다고 주장한다. 오직 이 방법으로만 pure한 가우시안 noise가 모델의 초기 샘플링 step 에 들어왔을 때, 그 모델이 inference 시에 input을 생성하도록 학습할 수 있다고 주장.
• 저자들은 Table 2. 에서 샘플링 스텝을 선택하는 두가지 추가적인 방법을 고려한다. Linespace는 iDDPM에서 제안. → 첫번째와 마지막 time step을 포함하고 중간 step들은 선형보간을 통해 선택. Trailing은 DPM에서 제안. 이는 마지막 time step만 포함하고 중간 step은 끝으로부터 짝수 step만 선택. 저자들이 선택한 샘플러 외에 다른거 선택해도 된다.
• S가 작을때 Trailing이 sample step을 더 효율적으로 선택하는 것을 발견. 그 이유는 t=1일때는 t=0일때와 비교해서 denosing하는 정보가 적고 별로 쓸모없는 step이라서.

Table 2.

• 저자들은 schedule을 Trailing으로 변경하고, DDIM 방식을 사용해서 Stable Diffusion과 같은 시행을 함

3.4. Rescale Classifier-Free Guidance

• 저자들은 terminal SNR이 zero로 갈때 classifier-free guidance (예: prompt)가 매우 민감하게 작용하여 image가 over-exposure 된다는 것을 발견. 이는 일반적인 문제임. 예를들어 Imagine에서 cosine schedule을 사용하는데, 여기선 over-exposure 문제를 해결하기 위해 dynamic thresholding을 사용.
• 하지만 Imagine의 방법은 image-space에서 사용가능하고 여기서 제안하는 것은 latent-space에서 생성 가능.
• (13) 일반적인 classifier-free guidance 에서의수식. $x_{p o s}$는 positive prompt를 사용한 모델 output $x_{neg}$는 negative prompt를 사용한 모델 output $x_{c f g}=x_{n e g}+w\left(x_{p o s}-x_{n e g}\right)$ (13)
  • 이때 w가 너무 크면 이미지 over-exposure(prior가 가지고 있는 정보를 어느정도 유지하며 생성하고 싶지만, 너무나 크게 훈련 시의 prompt와 이미지에 오버피팅 되는 문제 인듯!) 문제가 발생. 이를 해결하기 위해 아래와 같이 새로운 rescaling 방법 제시.
• rescaling
  $\sigma_{p o s}=\operatorname{std}\left(x_{p o s}\right), \quad \sigma_{c f g}=\operatorname{std}\left(x_{c f g}\right)$ (14)
  $x_{\text {rescaled }}=x_{c f g} \cdot \frac{\sigma_{p o s}}{\sigma_{c f g}}$ (15)
  $x_{\text {final }}=\phi \cdot x_{\text {rescaled }}+(1-\phi) \cdot x_{c f g}$ (16)
• (15)에서 classifier free gudiance 적용 전에 원래 분포의 std로 rescaling한다. $x_{cfg}$는 너무 (w, $x_{pos}$)에 과적합 되어있으니 $x_{pos}$의 std로 rescaling 해줌. → 하지만 지나치게 평범함. 따라서 (16) 처럼 다시 rescaling. w = 7.5, ϕ = 0.7에서 잘 작동하더라. 구현은 알고리즘 2. 를 보자

알고리즘 2.

4. Evaluation

• 저자들은 위에서 제안된 방법들을 적용하여 Laion데이터셋을 사용해서 Stable Diffusion 2-1을 파인튜닝 함. 50,000번 iteration 돌림. 제안된 방법들을 사용하지 않은 모델로 학습시킨 모델도 하나 만듬.

4.1. Qualitative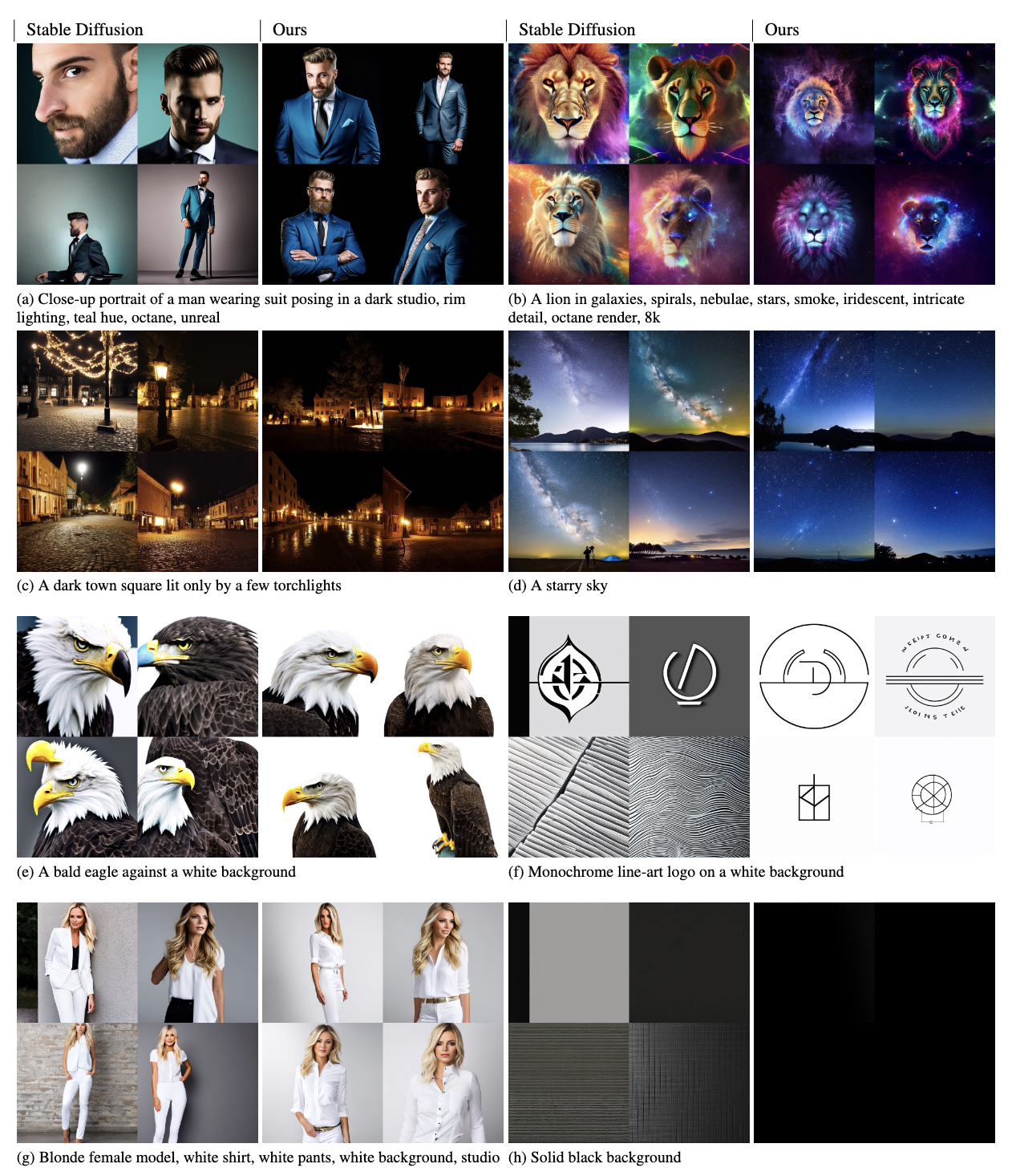

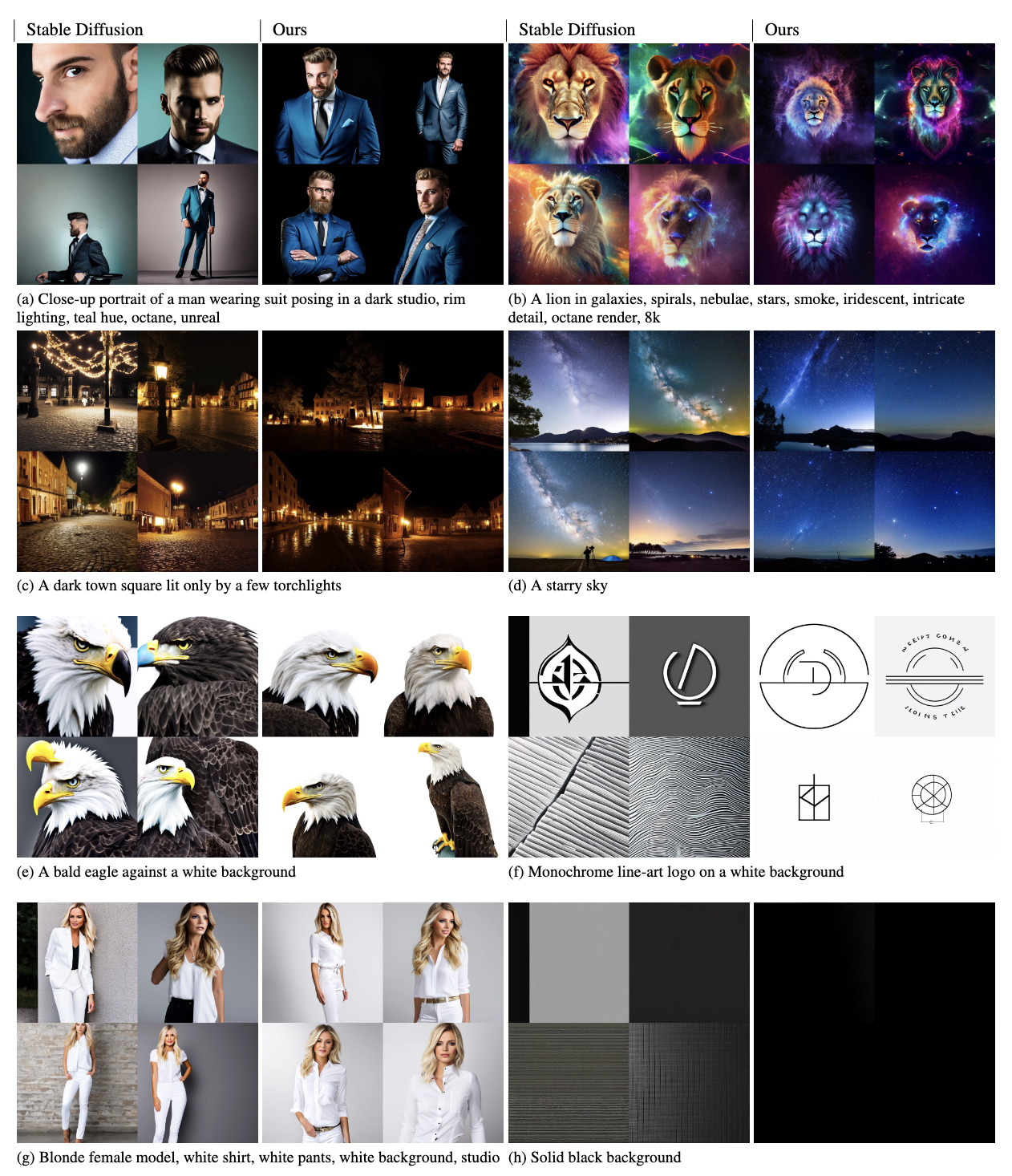
• 기본 모델은 white background, solid black background를 잘 잡아내지 못하는 반면 저자들의 모델은 잘 표현한다. 기본 모델은 일반적으로 중간 밝기의 이미지들을 생성하는 문제가 있다.

4.2. Quantitative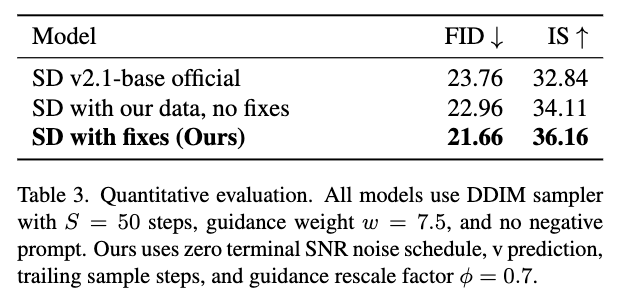

• FID와 IS Score도 일반 모델보다도 더 좋다.

5. Ablation

5.1. Comparison of Sample Steps

• S가 적을 때 Trailing 이 다른 schedule보다 특히 더 좋음. → 필자는 당연히 다른 schedule들은 time step 1을 포함하니까 안좋을 수 밖에 없다고 생각함.

5.2. Analyzing Model Behavior with Zero SNR

• 이상적으로 zero terminal SNR인 unconditional 모델이 있다고 할때, t=T에서 이 모델은, 노이즈에 관계없이 정확히 L2 mean(noise L2) 을 예측하는 법을 배운다. text conditional 모델에서도 노이즈에는 관계없이 정확히 L2 mean을 예측하는 법을 배운다.
• 즉 t=T에서의 첫번째 샘플 스텝은 정확한 다음 스텝을 예측하게 된다. variation은 두번째 스텝에서 부터 시작되는 것이다. DDPM에서는 $x_0$에서 가우시안 노이즈를 더해서 $x_1$를 만들고 DDIM에서는 동일하게 $x_0$를 예측하고 가우시간 노이즈가 추가 된다. $x_0$에 대한 posterior가 달라지게 되고 이제는 서로 다른 이미지들을 생성하게 된다. Figure 5를 보면, t=1000에서는 다 똑같은 이미지를 생성하고 변화는 다음 스텝부터 일어난다. → 아키텍쳐의 편의성을 제외하고선 사실 노이즈 입력이 필요없음.

5.3. Effect of Classifier-Free Guidance Rescale

• ϕ를 0.5~0.7이내로 정하는것이 가장 좋다고 함.

5.4. Comparison to Offset Noise

• 이 논문을 읽기전에 봤던 글이었는데, 이 논문에선 이 방법이 trick에 불과하다고 말하고 있음.
• Offset Noise는 Stable diffusion의 밝기 문제를 해결하기 위해서 채널별로 새로운 noise를 만들어 추가해주는 방법이다. 하지만 이 방법을 사용하게 되면 채널별로 noise가 주어지기 때문에 각 픽셀 별 noise는 더이상 iid가 아니게 된다. 그렇게 되면 노이즈가 낀 인풋은 실제 이미지의 평균을 나타낼 수 없게 된다. 따라서 모델은 학습할 때, 각 스텝에서 모델은 output을 예측할때 input의 평균을 따르지 않게 된다. 그럼 t=T에서 pure한 가우시안 노이즈가 주어지고 결함있는 noise schedule으로 인해 signal이 leaked 되더라도 모델은 이 signal을 무시히고, 모든 timestep에서 output mean을 자유롭게 변경한다.
• offset Noise를 사용하면 Stable Diffusion 모델이 매우 밝고 어두운 샘플을 생성할 순 있지만 이는 Diffusion process의 이론과 맞지 않고, 실제 데이터 분포에 맞지 않는 밝기의 샘플을 생성할 수 있다. → 근본적인 문제를 해결할 수 없는 trick이다.

6. Conclusion

• 정리하면, Diffusion 모델은 zero terminal SNR인 noise schedule을 사용해야하고, inference와 train이 align 되도록 t=T 인 last timestep에서부터 샘플링 해야한다고 주장.
• zero terminal SNR을 더 강제하기 위해서 기존의 noise schedule을 rescale하고, image over-exposure를 막기 위해 classifier-free guidance를 rescaling하는 기술을 사용하는 것이 좋다고 주장.
• and v prediction + v loss 사용

Appendix

• DDPM에서 zero SNR일때 division error가 나는 것을 해결하기 위한 방법 제시.
  DDPM, DDIM에서 v prediction을 사용하여 inference 수식 적용 방법.