DDIM 논문리뷰

Abstract

DDPM은 GAN없이 이미지 생성을 잘해냈지만, Markovian Process 라서 이미지 생성까지 많은 Step을 거쳐야 하기 때문에 시간이 너무 오래 걸린다. Sampling을 가속화하기 위해 non-Markovian diffusion process를 도입한 DDIM 제안 (DDPM과 같은 objective 사용). DDIM은 DDPM보다 10배에서 50배 빠르다. DDIM은 Deterministic하기에 Image interpolation이 가능하다. 또한 매우 적은 error로 reconstruction이 가능하다.

Introduction

DDPM과 NSCN은 adversarial Traning 없이 GAN과 상응할만한 샘플들을 생성했음. 하지만 NSCN의 ALD나 reverse process를 거치는 것이 GAN에 비해 속도가 너무 느리다. 이러한 속도 문제를 해결하기 위해 DDPM과 같은 objective를 가지고 학습되는 DDIM을 제안한다. 같은 Objectivte를 사용했기에 기존의 모델들을 사용 가능(Nosie 예측하는 UNET). DDIM에서는 Markovian process를 Non-Markovian으로 일반화한다.
DDIM을 사용하면 DDPM에 비해서 크게 세 가지 장점이 있다.
첫째는 10배에서 100배가량 DDPM보다 샘플링 속도가 빠르다.
두번째는 DDIM은 consistency property를 가진다. DDIM에서는 initial latent 에서 시작하여 샘플을 생성하면 매우 비슷한 결과가 나온다.
세번째는 이러한 consistency 덕분에 image를 의미있는 latent로 interpolation이 가능하다. -> (image Editing이 가능.)

Background

DDPM의 Objective

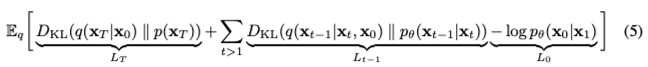
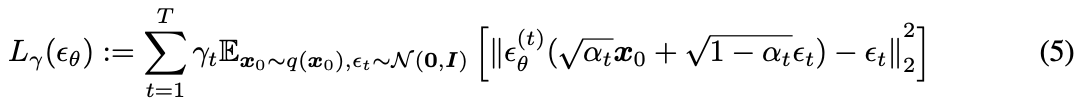
• Reverse Process $p^t_{\theta}(xt−1|xt)$
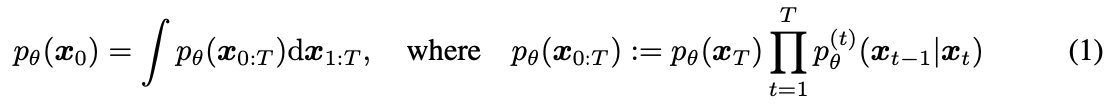
• Forward Process $q(xt|xt−1)$

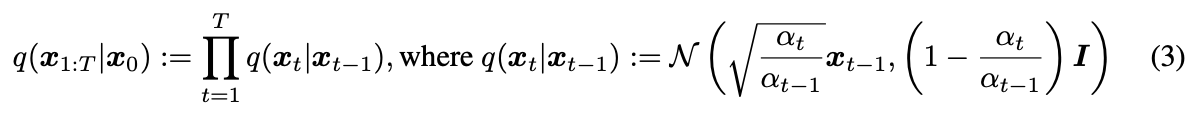
Variational Inference for Non-Markovian Forward Process

• $L_γ$가 marginal q(xt|x0)에는 의존하지만 joint q(x1:T |x0)에는 직접적으로 의존하지 않는 다는 것을 발견. 동일한 marginal을 가지는 joint가 많기 때문에 이를 만족하도록 새로운 Non-Markovian process 제안

• 아래 사진에서 오른쪽과 같은 Non-Markovian 제안
  

• joint 재정의

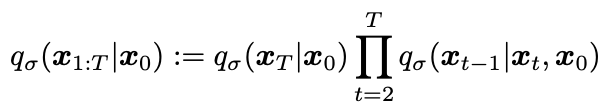
• marginal은 아래와 같음. -> DDPM과 DDIM 에서 동일
  

• 위 식을 만족하려면 $q_σ (xt−1 |xt , x0 )$는 아래와 같아야 함 : https://junia3.github.io/blog/ddim에 따르면 Bishop 책의 나오는 공식에 따르면 $x_0$를 넣었을 때 아래처럼 식이 나온다고 한다.

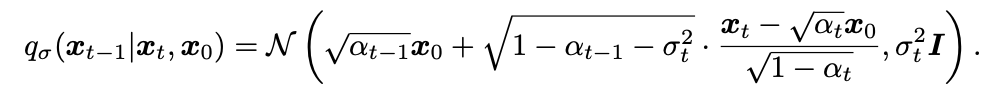
• appendix에서 나오는 식에 가우시안 pdf 넣어서 계산하면 나올것 같다.... 사실 잘 모르겠다!!

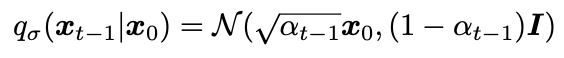
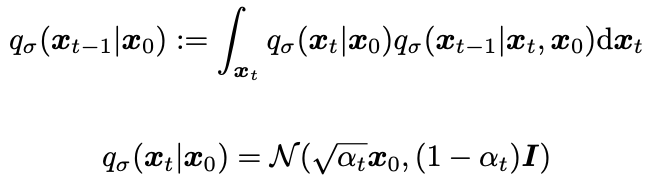
• 공식을 못찾겠어서,, 아래 수식을 따라가보니 이해할 수 있더라!! (cvpr diffusion tutorial)

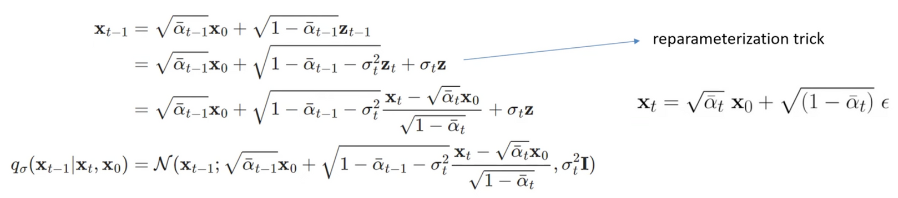
• $q_σ (xt−1 |xt , x0 )$ 식에서 bayes rule 적용하면 Non-Markovian forward process를 얻을 수 있음.

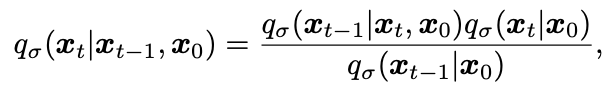
• DDPM과 달리 $x_t$는 $x_{t-1}$과 $x_0$에 의존하기 때문에 forward process는 더이상 Markovian process가 아니다. σ는 forward process가 얼마나 stochastic한지 조절하는 척도이다. σ가 0이되면 $x_{t-1}$과 $x_0$이 주어지면 $x_{t}$는 고정된다.

Generative Process and Unified Variational Inference Objective

DDIM에서는 $x_t$가 주어지면 $x_0$를 예측하고, $q_σ (xt−1 |xt , x0 )$를 이용해서 $x_{t-1}$ 를 예측한다.

denoised observation

• $x_t$ 수식
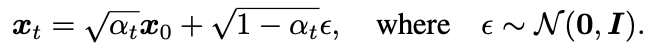
• 위 수식을 조금 수정해서 아래와 같이 $x_t$가 주어지면 $x_0$를 예측한다.
  

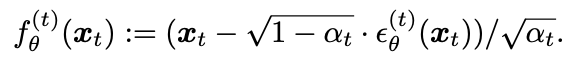
define the generative process

• $x_t$와 $x_0$로 부터 $x_{t-1}$ 예측. 아래 수식에서 t가1일때 generative process가 supported 되게 하기 위해서 분산 term을 추가했다는데,, 이부분 이해가 잘 안된다. 분산 term이 없으면 왜 support가 안되는 거지..?

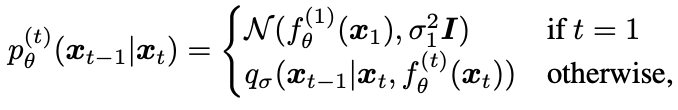
Objective

• objective 수식을 풀게 되면 최종적으로 σ에 의존한 objective가 나온다. 여기서 σ가 0이면 DDIM, 0이 아니면 DDPM으로 볼 수 있다.
• 아래 사진은 DDPM objective

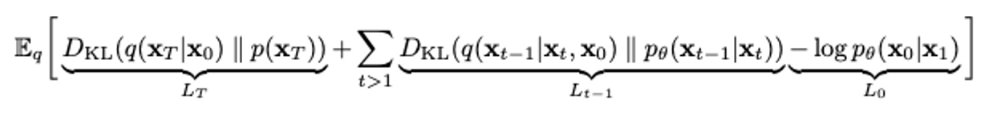
Theorem 1

• $L_{1}$은 DDPM의 최종 variational lower bound이다.
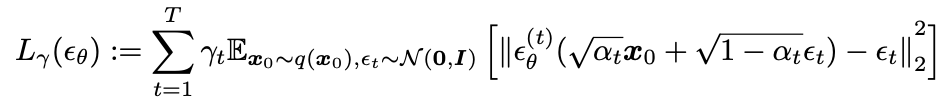
• $L_γ$는 모델 ε(t)의 매개변수 θ가 서로 다른 t에 걸쳐 공유되지 않는 경우, εθ에 대한 최적의 솔루션이 가중치 γ에 의존하지 않는다는 점에서 특별하다. 아래 Theorem에 따르면 objective 최적화 관점에서 $J_{σ}$=$L_{γ}$ 이므로 $J_{σ}$의 최적의 solution은 $L_{γ}$에서 γ=1때의 값과 같다(DDPM에서 ). 따라서 매개변수가 모델 εθ의 t에 따라 공유되지 않으면 DDPM의 objective인 $L_1$를 $J_{σ}$로 그대로 사용해도 된다.

Sampling from Generalized Generative Process

Denoising Diffusion Implicit Model

• $L_1$을, Markovian Forward 또는 non-Markovian Forward를 사용하며 최적화 할 수 있다. 따라서 Pre-trained 된 DDPM 모델을 그대로 사용하고 σ를 변경하여 더 나은 생성 프로세스를 찾는 데 집중 할 수 있다. 즉 DDPM으로 학습된 UNET을 그대로 이용하며, sampling 방식만 DDIM 방식으로 바꿔서, 빠르게 샘플링이 가능하다.
• 일반적으로 DDPM으로 학습하고 DDIM으로 inference하는 것이 좋다고 한다.
• $x_{t-1}$을 샘플링 하는 식은 다음과 같다.
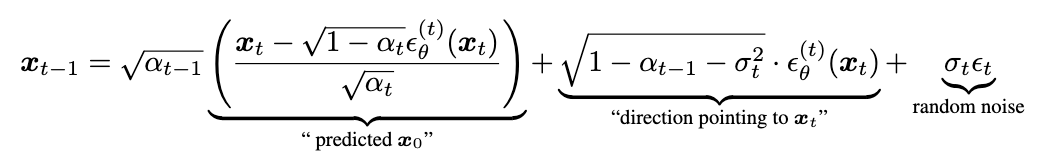
• 모든 t에 대해서 $σ_{t}$=0 이면 forward processs가 $x_{t-1}$, $x_{0}$에 대해서 deterministic 해진다. (t=1일 때 제외)
• 모든 t에 대해서 $σ_{t}$=$\sqrt{(1-\alpha_{t-1})/({1-\alpha_{t}})}$$\sqrt{(1-\alpha_{t})/({\alpha_{t-1}})}$이면 DDPM과 같다

Accelerated Generation Processes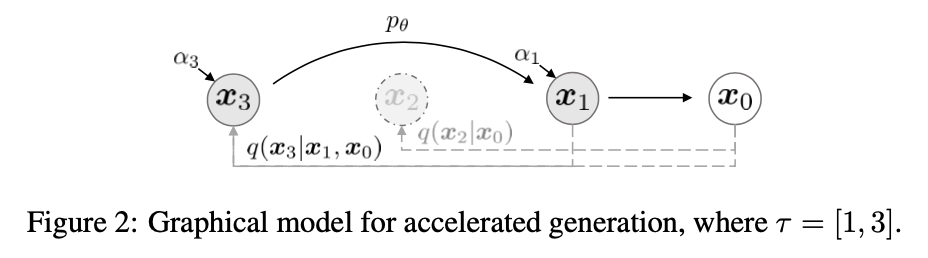

• $L_1$은 $q_σ (xt| x0 )$가 고정되어 있는 한 특정 forward process에 의존하지 않으므로 T보다 길이가 작은 순방향 프로세스를 고려할 수도 있다. -> σ를 0으로 줘서 deterministic하게 주면, 특정 forward에 종속되어 있지않고 독립적이기 때문에 T보다 길이가 작은 forward, reverse를 사용할 수 있다.
• 샘플링할 [1, , ,T]의 sub sequence [$τ_1$, , ,$τ_S$]를 sampling trajectory라고 정의 하자. 이때 sampling trajectory의 길이가 T보다 작으면 계산 효율성이 크게 향상된다.
• DDIM의 방식처럼 임의의 step의 forward step에서만 모델을 훈련시키는 것보다 DDPM처럼 모든 step에 대해서 모델을 학습시키는게 더 효과적이다는 것이 알려져있다. -> 따라서 DDPM의 UNET을 이용하고 DDIM의 방식으로 sapmling을 하는 것이 좋다.

Relevance to Neural ODEs

• 이 부분 어렵다..

• Eq 12를 아래와 같이 ODE를 풀기 위한 Euler integration 으로 나타낼 수 있다.
  

• reparamiterization을 통해 다음과 같이 ODE로 나타낼 수 있다.

• 이는 충분한 discretiatoin step를 통해 x0을 xT로 인코딩하고 Eq에서 ODE의 reverse를 simulation하는 생성 프로세스(t = 0에서 T로 이동)를 reverse시킬 수도 있음을 시사한다. -> $X_0$를 $X_T$로 보낼 수 있음.

• 이는 DDPM과 달리 이미지를 latent로 inversion이 가능하고, 이를 통해서 downstream application에 유용하게 쓰일 수 있다. (Image Editing 등)

• 아래 수식을 참고하자. 출처

Experiments

• η가 1이면 DDPM, 0이면 DDIM이다.
  

Sample Quality and Efficiency

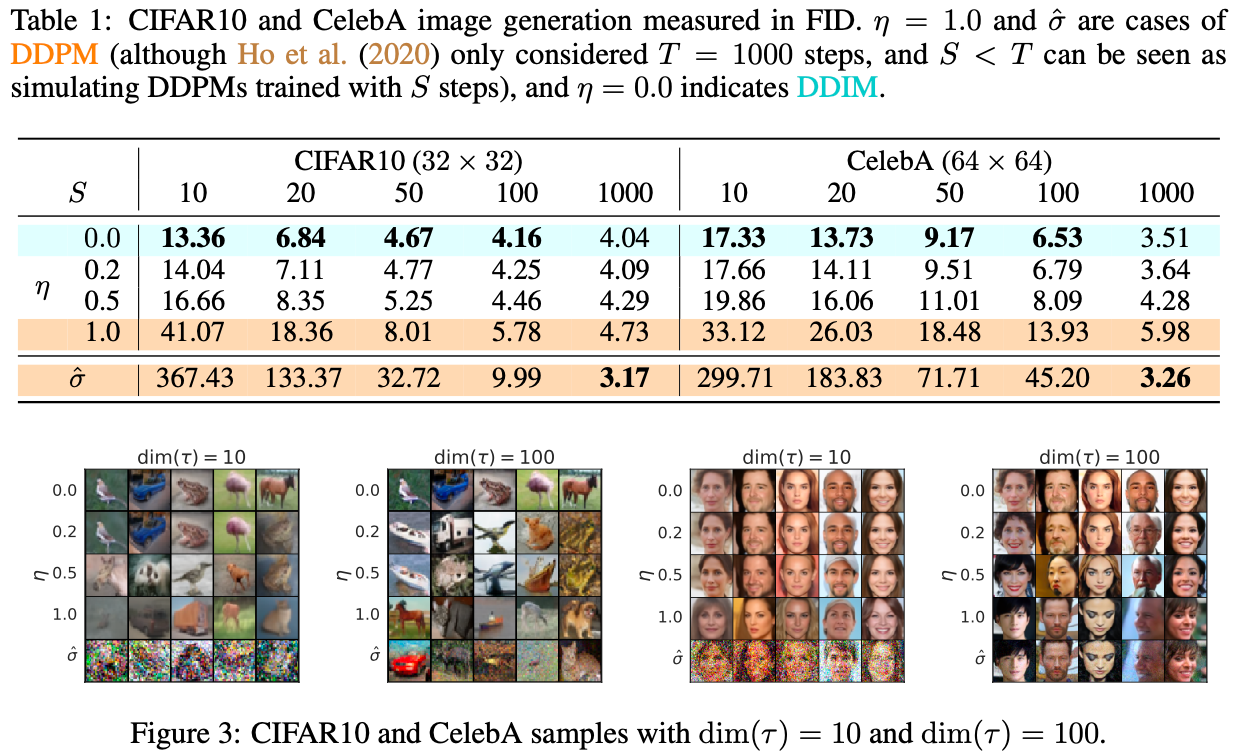
• τ(step 수)를 키울수록 성능이 좋아진다. 또한 step이 적을때 DDPM에 비해서 DDIM이 훨씬 성능이 좋다.
• ($\hat{\sigma}$과 η가 1일때는 $\sigma$ 수식이 살짝 다르다.)

Sample Consistency in DDIMs

• DDIM은 generative process가 deterministic하다.
  

• ${X_T}$에 따라서 생성 과정 중의 특정 step을 뽑아봐도 모두 하나의 이미지로 생성되는 것을 볼 수 있다.

Interpolation in Deterministic Generative Processes

• 사진은 Latent상에서 ($X_T$) 간단한 Interpolation이 두 샘플 간의 의미상 의미 있는 Interpolation으로 이어질 수 있음을 보여준다. -> DDIM은 DDPM이 제어할 수 없는 latent를 통해 high-level에서 이미지를 control 할 수 있다.
  

Reconstruction From Latent Spcae

• DDIM에서는 ODE로 Euler intergration을 하기 때문에 $X_0$를 $X_T$로 encoding (inversion)이 가능하다 이후 다시 $X_0$로도 recon이 가능하다

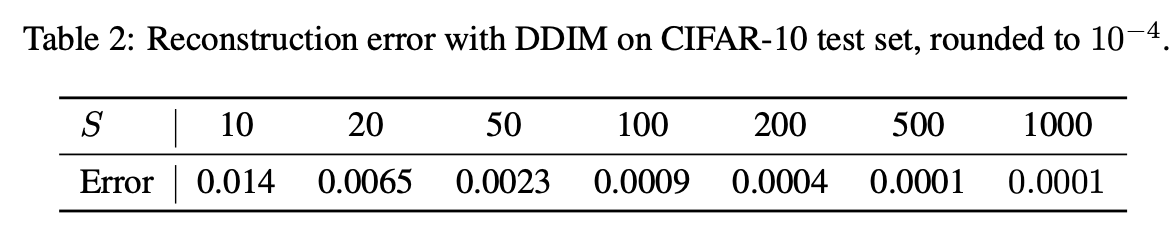
DDIM 정리하면..

1. DDIM은 DDPM보다 훨씬 더 적은 step으로 이미지 생성이 가능하다. (10~100배 더 빠름)
2. DDIM은 생성과정이 Deterministic하다. -> 반대로 inversion도 가능하다.
3. DDPM과 다르게 한번 initial latent variables 가 fix 되면, generation trajectory와 상관없이 항상 high-level의 이미지를 생성할 수 있으며 latent space 상에서의 interpolation도 가능하다.
4. latent에서 이미지 recon도 가능하다. (DDPM은 stochastic한 term이 이미지 생성 과정에 있었기 때문에 recon이 불가능 했음. -> $X_T$가 같은 $X_0$로 가지 않음)