Denoising mcmc for accelerating diffusion-based generative models 논문 리뷰
Dfifusion
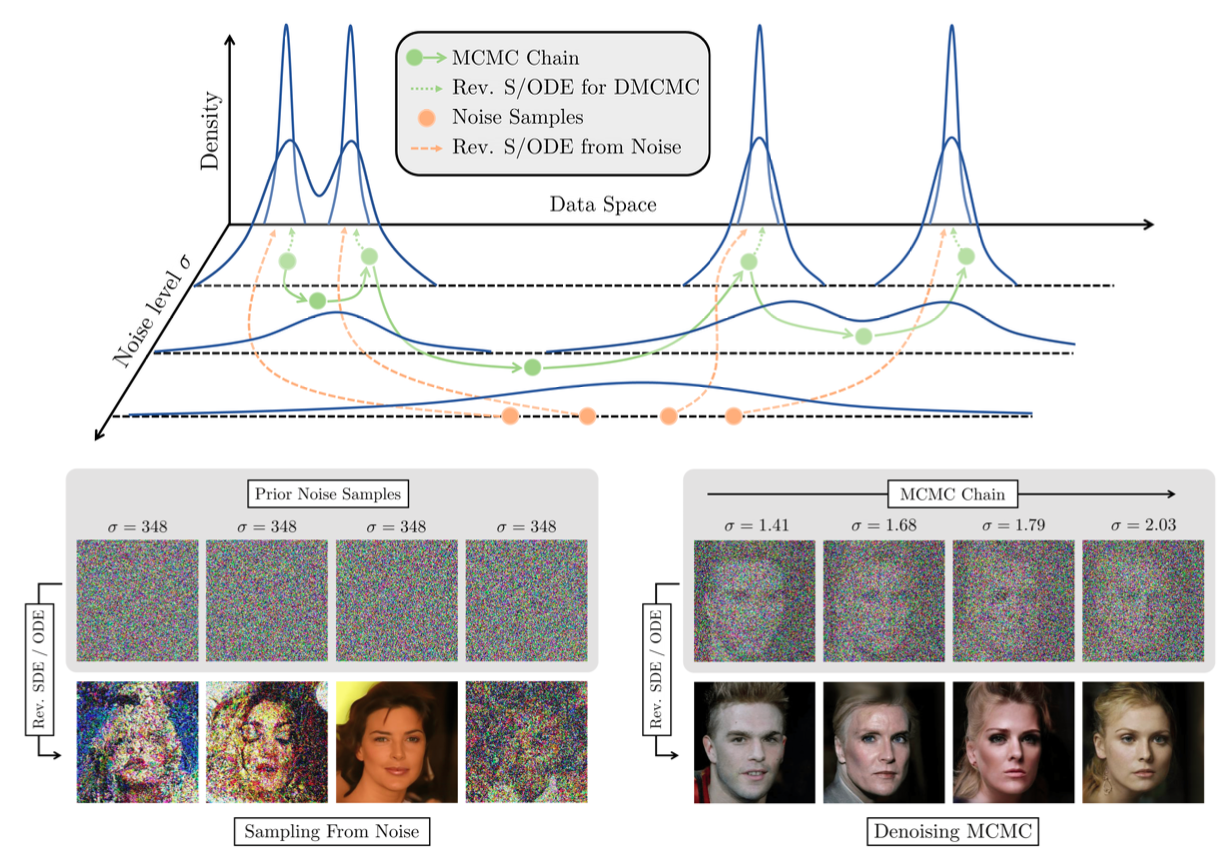
이 논문은 위 그림만 이해하면 어느정도 다 이해했다고 봐도 된다고 생각한다.
초록색 실선이 이 논문에서 제안하는 DLG의 Step1인 MCMC ON THE PRODUCT SPACE X × S 부분, 초록색 점선이 Step2인 INCORPORATING DENOISING STEPS이다.
아래 설명에서 Gibbs Sampling은 기존의 Score Network로 X를 예측하고, 새로 제안한 Noise Classifer로 σ를 예측하는 것을 의미. (Product Space에서 샘플링)
1. 초깃값(가장 왼쪽위의 초록색 점)을 설정하고 MCMC를 거친다. 코드에서는 cifar10 데이터 셋에서 20번의 Gibbs Sampling을 통해 초깃값을 설정했다.
2. Noise level이 낮은 부분(Data Manifold와 가까운 곳)에 초깃값을 설정하고 MCMC(Gibbs sampling으로) 여러번 수행. 코드에서는 10번 수행했음. 그 후 Noise 레벨이 가장 적은 Data(x, σ)를 선택.
3. 선택된 Data를 기존의 SDE/ODE Integrators를 사용하여 최종 Data 생성.
Contribution
-
X(Data)와 σ(noise level)의 product space 에서 score-based sampling을 진행하는 방법론인 DMCMC (Denosing MCMC) 제안 → 모든 MCMC, VE(Variance Exploding) process noise-conditional score function, reverse-S/ODE integrator 들을 pulg and play 방식으로 사용가능.
-
DMCMC의 Instance로 DLG(Denoising Langevin Gibbs) 제안한다. DLG는 2가지 step으로 이루어져 있음. step 1은 product space 에서 MCMC를 수행하여 샘플들 {( , )} 을 생성하는 것이고, step 2는 MCMC를 수행하여 생성된 샘플을 reverse-S/ODE integrator를 사용해 reverse-S/ODE solve 하는 것이다. DLG의 MCMC 부분은 Langevin Dynamics을 사용한 데이터 업데이트 단계와 noise level prediction step를 번갈아 가며 수행.
여기서 reverse-S/ODE solve 한다는 것은 t = 에서 t = 0로 가면서 으로 부터 를 생성하는 것을 의미. -
DLG는 제한된 NFE(number of score function evaluation) 에서 6가지 reverse-S/ODE integrators에서 좋은 결과를 냈다. → 샘플링 속도가 빠름.
Background
1. Denosing Score Matching
-
Score 추정을 하기 위한 방법론으로 처음 제안된 Loss. 2005
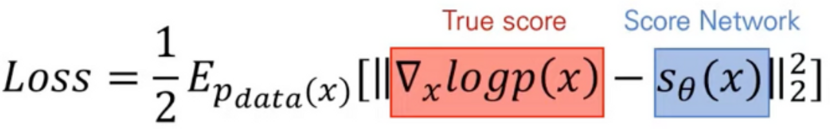
-
Score 추정을 하기 위하여 아래 수식과 같이, Data 에 noise를 랜덤하게 추가해서 x을 만들고, 이를 이용하여 True score를 예측하고자 함. noise가 매우 작다면 score network () 가 True score와 같아짐. 2011
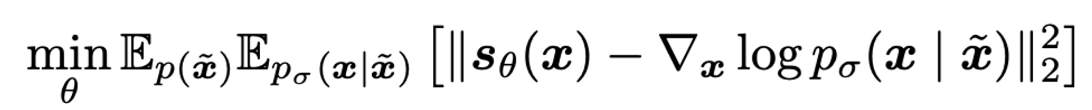
2. NCSN
- Generative Modeling by Estimating Gradients of the Data Distribution (2019) 에서 제안한 Noise Conditional Score Networks → Noise에 따라서 Score를 예측하게 만들어 Data Distribution이 적은 곳에서 부정확했던 Score 예측을 정확하게 만들어줌. 2019

3. Markov Chain Monte Carlo (MCMC)
-
MCMC는 이전 step에만 의존하는 그 다음 step의 데이터를 샘플링하는 방법이라고 생각하면 된다. 유명한 Socre-based MCMC 방법으로는 Langevin Dynamics (아래 수식)가 있다.
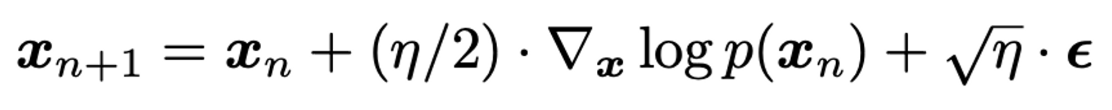
-
Annealed Langevin Dynamics는 Noise 크기를 감소시키면서 sampling을 하는 방법을 의미. 2019 -> DDPM에서 Beta schedule과 유사하게 작동된다고 생각 할 수 있음.
4. Diffusion Models
-
Diffusion SDE
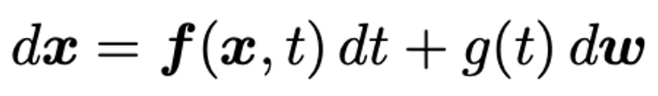
-
Reverse SDE
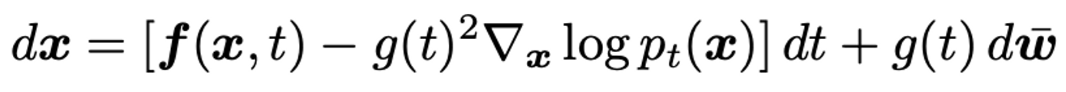
-
Reverse ODE
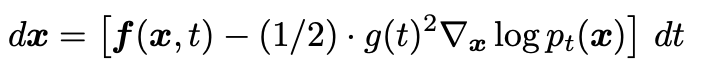
-
하나의 Diffusion SDE에는 항상 하나의 Reverse SDE가 존재한다. 하나의 Reverse SDE에는 하나의 deterministic한 Reverse ODE가 존재함. (랜덤성을 주는 브라운 운동 텀이 사라짐) Reverse ODE의 특별한 Case가 DDIM.
-
reverse-S/ODE를 solve 하여 를 생성해낸다.
DLG
Step1 : MCMC ON THE PRODUCT SPACE {X × S}
-
기존의 Langevin Dynamics 방법들은 noise scale 이 정해져있거나, noise schedule 이 정해져 있었다. 그 상태에서 x만 샘플링 하면 된다.
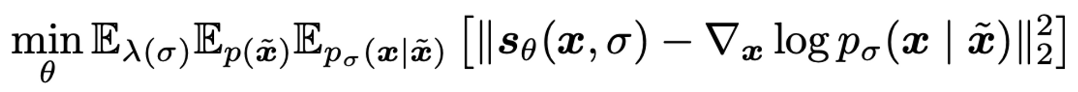
-
하지만, DMCMC는 data X와 noise σ을 함께 샘플링 해야하므로 Score matchig 이 아래와 같이 달라진다.
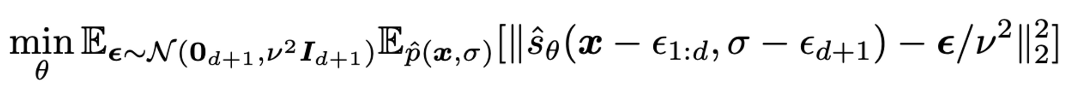
-
따라서 기존의 Pretrained Score model을 사용하여 샘플링하는 것이 불가능하다. 이 문제점을 Gibbs Sampling을 이용해서 해결한다. Gibbs Sampling을 이용해서 를 고정하고 만 업데이트 하여 를 생성하고, 를 고정하고 만 업데이트 하여 을 생성한다.
Updating x
- 기존의 Langevin Dynamics 를 이용해서 X를 업데이트 한다.
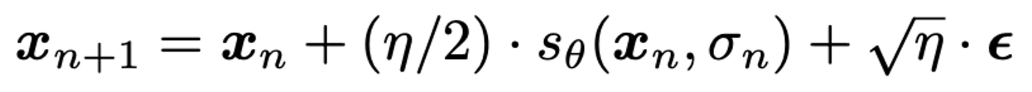
Updating σ.
- σ를 업데이트 하기 위해서 noise-level classifer 를 제안한다. 이는 를 입력으로 받아 를 생성해주는 간단한 DNN (코드보면 간단한 CNN으로 구성되어 있음)이다. 아래 objective로 학습된다. -> x가 주어지면 σ를 예측하도록 학습.

Step2 : INCORPORATING DENOISING STEPS
- 기존의 Solver들을 사용해서 최종 샘플 생성
정리
실험 결과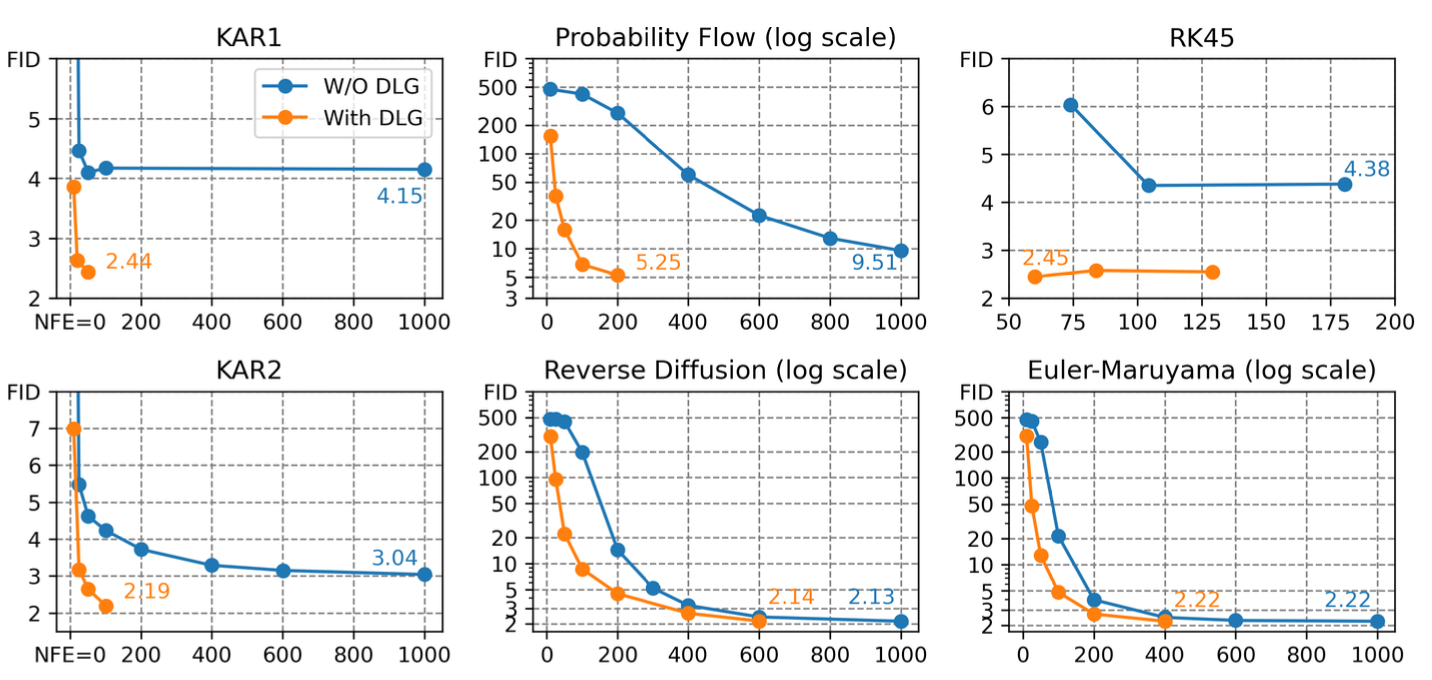
- 코드
아이디어가 신기하고 어려웠던 논문
