[DB] Closure of Functional dependencies

$F^+$를 구하는 방법을 자세하게 알아보자.

Armstrong's Axioms

$F^+$를 구하기 위한 암스트롱의 공리를 알아보자. 이 공리를 계속해서 적용하면 $F^+$를 구할 수 있다.

• if $\beta \subseteq \alpha$, then $\alpha \rightarrow \beta$ (reflexvity)
• if $\alpha \rightarrow \beta$, then $\gamma\alpha \rightarrow \gamma\beta$ (augmentation)
• if $\alpha \rightarrow \beta$, and $\beta \rightarrow \gamma$, then $\alpha \rightarrow \gamma$ (transivity)

이 공리들을 적용한 함수 의존성 F에 적용한 결과들은 항상 참이다. 함수 의존성 집합 F가 가지는 것들에서만 파생된다. 또한 F가 가질 수 있는 모든 경우의 수를 보일 수 있다.(trivial한 것도 포함한다.)

Algorithm

간단하다. F에 대해 reflexity와 augemntation을 모두 적용하고, 이에 대해 transivity를 적용한다. 이를 계속해서 반복하여 F가 변하지 않을때 알고리즘은 종료된다.
알고리즘의 최악의 경우에 약 $2^{2n}$만큼 소모된다.(시간 복잡도 $O(2^{2n})$)

Additional rules

$F^+$를 구하기 위한 추가적인 rule은 다음과 같다.

• if $\alpha \rightarrow \beta$ holds and $\alpha \rightarrow \gamma$ holds, then $\alpha \rightarrow \beta\gamma$ holds (Union)
• if $\alpha \rightarrow \beta\gamma$ holds, then $\alpha \rightarrow \beta$ holds and $\alpha \rightarrow \gamma$ holds (Decomposition)
• if $\alpha \rightarrow \beta$ holds and $\gamma\beta \rightarrow \delta$, then $\alpha\gamma \rightarrow \delta$ (Pesudotransitivty)

Closure of Attribute Sets

F attribute set인 $\alpha$의 closure인 $\alpha^+$를 구할 수 있다.

여기서 closure $a^+$는 $\alpha \rightarrow \beta$에서 모든 $\beta$의 집합이다.

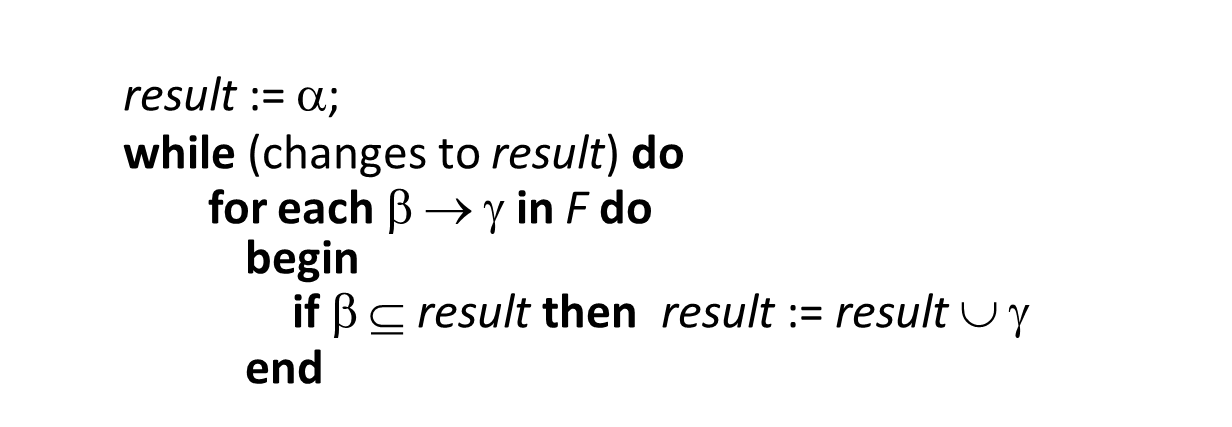
위와 같이 알고리즘이 정의되며, 모든 $\gamma$에 대해한 합집합으로 $a^+$가 정의된다.
시간 복잡도는 최악의 경우에 $n^2$가 된다.

얘네는 attribute가 superkey인지 확인할 때 사용한다.