Floating Point
Before getting in
C언어에서 실수를 저장하는 방법을 알아보자. 프로그래밍 언어마다 다를 수 있겠지만, 원리는 비슷하기 때문에 새로운 프로그래밍 언어를 배워도 해석하기 수월할 것이다.
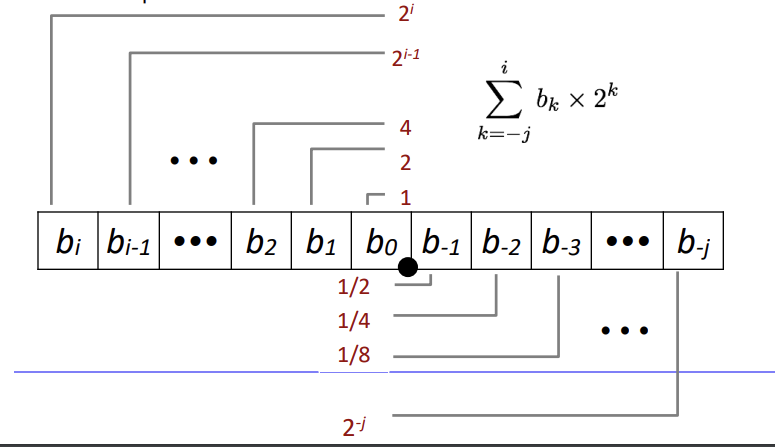
컴퓨터 내부는 전부 2진수로 되어 있다고 한다. 10진수를 2진수로 저장하는 방법은 위와 같이
2^i * (1 or 0)로 표현된다. 정수부일 경우 i > -1, 실수부일 경우 i < 0이다.
Fixed Point Represention
2진수로 10진수를 저장할 경우 두 가지 문제에 직면한다.
첫 번째는 큰 수와 작은 수를 저장하는데 제한이 있다는 것이다. 2진수로 10진수를 저장할 경우 결국 2의 n승 더해서 만들어야 하는데, 이는 3.4375와 같은 10진수도 11.0111와 같이 굉장히 긴 2진수로 저장해야한다. 0과 1로만 표현을 하므로 길이가 더 길어지고 길이가 더 길어진다면 저장할 공간이 더 필요하게 된다.
두 번째로 0.1과 같은 수를 표현하지 못한다. 2의 제곱수로만 표현되므로 근삿값이 저장된다.
이러한 제한이 있지만 효율적으로 저장하는 IEEE standard를 알아보자.
Standard IEEE 754
Standard IEEE의 ploating point의 form을 알아보자.
32bit float type으로 알아보겠다.
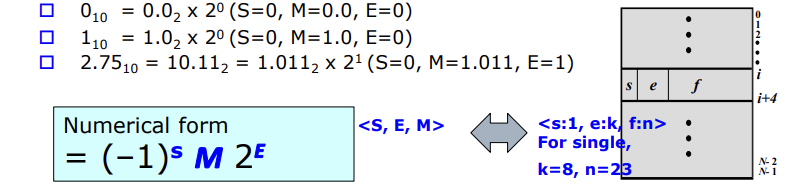
- S(Sign)는 bit의 맨 앞에 있는 수로 부호를 결정한다. 0은 양수이고 1은 음수이다.(1bit)
- M(Mantissa)은 value의 range를 뜻한다. 10진수를 2진수로 변환하고 변환한 2진수를 2^0자리 까지만 남긴다.(ex) 1.0101) 이 값이 Mantissa이다.
- E(Exponent)는 자리수를 뜻한다. M의 이전 값 101.01을 1.0101로 변환한다면 2^2를 곱해줘야한다. 2^n에서 n을 뜻 한다.(23bit)
10진수 2.75는 2진수로 10.11이다. 2.75는 양수이니 S(sign)가 0이고
M은 1.011이 된다. M(Mantissa)부분은 위와 같이 2미만의 실수가 된다
그리고 손쉽게 E(exponent)가 1.011 * 2^1이므로 E가 1인 것을 알아차릴 수 있을 것이다.
결론적으로 S=0, M=1.011 E=1이 된다.
Normalized form
Mantissa
Mantissa에 값을 저장할 때 10진수에서 변환한 2진수를 2^0까지 남겨놓고 그 이후의 소수점 아래의 값들만 저장한다.f에 저장
ex) 십진수 1.5을 이진수 1.1 변환하고 1만 저장한다.
왜냐하면 2^0자리는 기존의 10진수가 0이 아닐 경우 무조건 1일 것이다. 1을 저장해버리면 1 bit의 손실이 일어난다. 2^0을 저장하는 대신 연산 중에 1을 더해주는 것이 이득일 것이다. 0은 따로 처리해주면 된다.
1.0은 0만 저장하면 된다.
Mantissa는 변환값, f는 저장값이다.
Exponent
4byte의 Float type(C언어)을 알아보자.
10진수 1.0을 Float type에 저장하려면 어떻게 해야할까?
S, M, E은 각각 0을 저장한다는 사실을 눈치챌 것이다. 그런데 E가 0이라고 0을 저장하는 것은 아니다.
E는 8bit이다. C언어에서의 8bit인 signed char은 -127, -128을(이둘은 예외로 사용.) 제외하고 [-126, 127]까지의 수를 저장한다. 여기서 127을 이용하여 값을 bias로 사용하여 저장한다. -127과 -128이 제외된 이유는 1111 1111(255 - 127 => 128 = -128)과 0000 0000(0-127=>-127)은 다른 수를 저장하기 위해 이미 예약되어 있다.
127을 bias로 사용한다는 말은 E = e - 127의 식을 이용하여 e의 값을 저장한다. E가 0이기에 e는 127이 된다. 그렇다면 E를 위해 저장되는 e값은 127 즉, 0111 1111이 된다.
E는 변환값, e는 저장값이다.
float에 저장된 1.0(10진수)

1521310(10) = 111011011011012(2) = 1.1101 1011 0110 1 x 2^13
위의 값을 float type에 저장해보자.
그럼 S는 0 M은 1101 1011 0110 1000 0000 000이 될 것이다. E = 13이고 e는 13 + 127인 140이 될 것이다. 그럼 140은 signed로 보았을 때 0111 1111 + 0000 1101 = 1000 1100가 된다. 두 번의 float type 저장으로 아래의 결과가 도출된다.

- C언어의 float type은 n승을 unsigned char의 형태로 저장한다.
- 그렇다면 e는 unsigned이다. E를 구하기 위해서 bias를 빼주어야 한다.
127은 unsigned type에서 0이니 signed char type인 13에 127을 더해 unsigned로 만들어 주는 것이다. 힘들다..
Double type
Double type은 float과 거의 비슷하다. 저장할 수의 크기와 bias가 커진다.
Difference
- S(1bit), F(52bit), E(11bit)
- bias = 1023(11bit) signed 11bit => [-1022, 1023]
- E = e - 1023(float과 같이 계산시 signed -> unsigned)
Exceptions
Largest Normalized Value
0 / 1111 1110 / All 1s in 33 bit
M = 1.1111111~1 2와 가까운 수이다.
E = e - bias = 254 - 127 = 127: 127 승이 최대이다.
그럼 최대값은 2 * 2^127 = 2^128에 근사한다.
Smallest Normalized Value(절댓값)
0 / 00000000001 / All 0s in 33 bit
M = 1.000~0 1이다.
E = e – bias = 1 – 127 = –126
그럼 최소값은 1 * 2^-126이 된다.
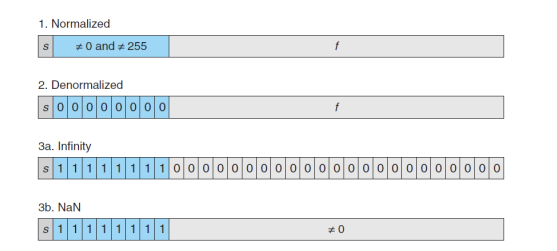
Denomarlized
실수 0은 e가 모두 0일 때이다. e가 0일 땐 E가 -127이지만 -126으로 처리해준다. e를 1로본 것이다.
그리고 M에 1을 더해주지 않는다. 그럼 0^-126이기에 0이다. Integer type의 0과 같다.
이렇게 0은 e가 모두 0일 때만 가능하다.
Sign이 0이던 1이던 모두 정수 0값과 동일하다.
Infinity
무한대값은 모든 e와 f 모두 1일 때이다. e가 모두 1일 때는 255이다. -127을 더해주면 128이란 값이 나오고 이는 signed char로 계산했을 시 -127이된다. -127승으로 사용하지 않고 예외로 처리하여 Infinity로 사용한다.
이는 실수 값을 0으로 나눌 때 발생한다. ex) 1.0 / 0.0
그렇다면 unsigned char의 최대값인 255를 사용하지 않고 예외로 처리한 것이다.
Sign에 따라 양의 무한대, 음의 무한대 표현이 가능하다.
NaN
NaN값은 숫자가 아니란 뜻이며 e가 모두 1 f가 모두 0일 때의 값이다.
이는 무한대끼리의 연산, 허수(sqrt(-1)), NaN의 연산, 초기화되지 않은 데이터를 포함한다.
Rounding
Rounding to even

읽어보면 이해하기 쉬울 것이다.
half way인 경우, 100일 때 바로 앞 비트가 1이라면 올림을 했을 경우 2(even)으로 set되기 때문에 올림을 수행한다. 반대로 0일경우 1(odd)로 set되기 때문에 내림을 수행한다. 이를 halfway에서 rounding to even이다. halfway가 아닐 경우 반올림을 수행한다.
casting

int에서 float타입은 float의 mantissa가 23bit이기 때문에 round가 일어난다.(반올림)
int에서 double type의 casting은 완벽하게 변환이 가능하다.
double/float에서 int는 대개 overflow가 나서 Tmin으로 set된다.
실수부는 무조건 0으로 내림된다.
예시를 보면 float에 round가 일어났다. 값이 그대로 전달되지 않는다.
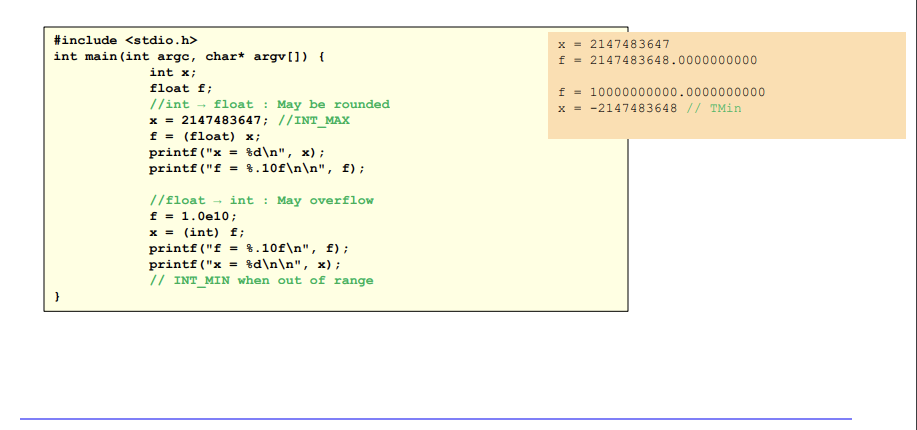
위의 이미지는 matissa 부분이 부족하여 반올림 되는 모습을 볼 수 있다(int->flaot)
int가 담아내지 못하는 수는 overflow가 일어나 Tmin으로 set된다.

너무 작은 부분을 더한다면 mantissa 부분이 부족하여 반올림되어 버려진다.
3.14f와 1e20을 더한다면 3.14f가 버려진다. 그리고 -1e20 더하기 때문에 0이란 결과가 나온다.
그 밑은 1e20자체가 라운딩되어 굉장히 작은 값을 출력하는 모습을 볼 수 있다. 값이 아예 같지 않은 것이다.