[Computer Architecture] Hardware for FP & Instructions of FP

Float Multiplication

소수점 곱셈은 다음과 같은 방식으로 이루어진다.

$1.000 \times 2^{-1} \times -1.110 \times 2^{-2}(0.5 \times -0.4375)$

• exponent를 더한다
  unbiasedd: $-1 + 3 = -3$
  biased: $(-1 + 127) + (-2 + 127) = -3 + 254 - 127 = -3 + 127$
• significands를 곱한다.
  $1.000 \times 1.110 = 1.1102 = 1.110 \times 2^{-3}$
• Normalize & check for over/underflow
  $1.110 \times 2^{-3}$ no change
• Round and remormaiize
  $1.110 \times 2^{-3}$ nochange
• sign을 정한다.
  $-1.110 \times 2^{-3} = -0.21875$

Float Addition

소수점 덧셈은 다음과 같은 방식으로 이루어진다.

$1.000 \times 2^{-1} \times -1.110 \times 2^{-2}(0.5 + -0.4375)$

• exponent를 맞춘다.
  exponent가 더 작은 수를 Shift left 하고 두 값을 더한다.
  $1.000 \times 2^{-1} + -0.111 \times 2^{-1} = 0.001 \times 2^{-1}$
• Normalize & check for over/underflow
  $1.000 \times 2^{-4}$ no change
• Round and remormaiize
  $1.000 \times 2^{-4}$ no change

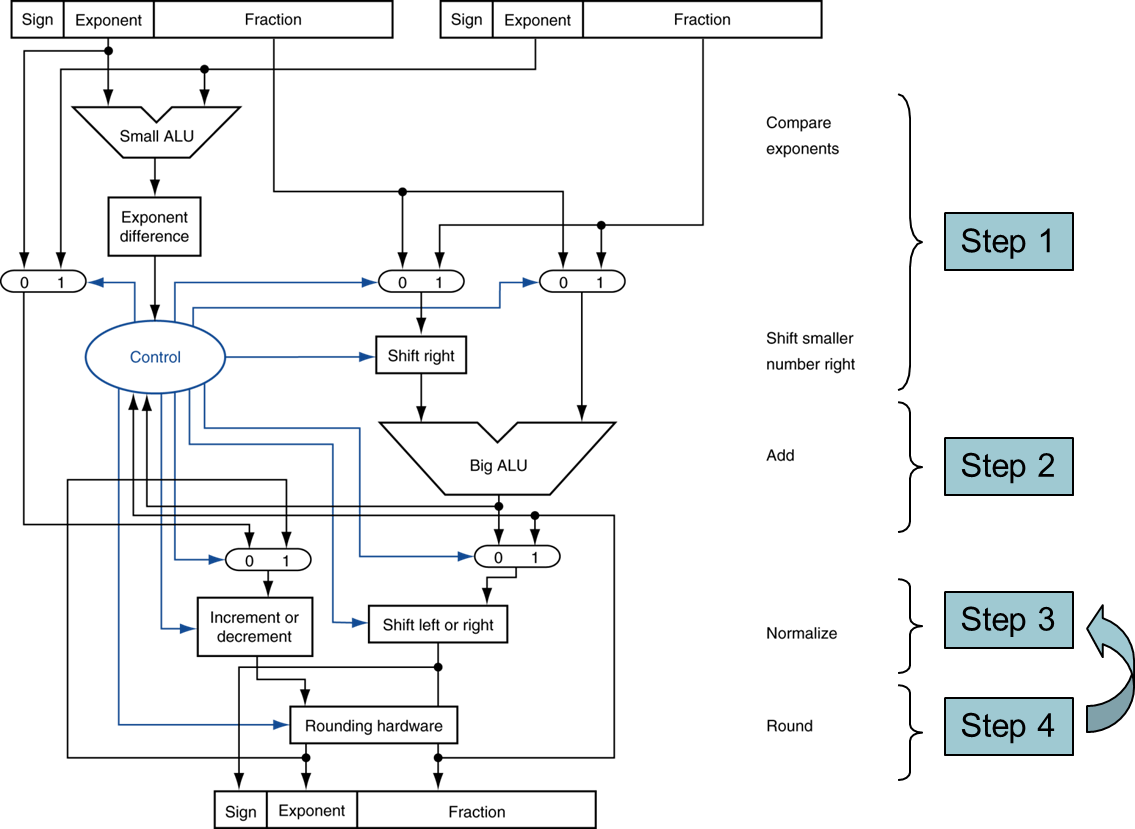
왼쪽 double을 A 오른쪽을 B라 하겠다.
(0 1) 처럼 생긴 것은 두 input 중 하나를 고르기 위해 존재하며 MUX라 불린다.
A가 0, B가 1이며 여기에 0 또는 1 신호를 보낸다. 단순하게 & 연산과 같이 0, 1을 출력한다.
예를 들어, exponent가 A<B 인경우 A를 shift right 해야하기 때문에, A를 선택하기 위해 0을 줘야한다.

차례대로 step으로 알아보자.

• Step 1. Small ALU를 통해 A-B(exponent)를 수행한다. Exponent difference를 통해 어떤 값이 더 작은지 계산한다.
  그리고 Control은 exponent 중 어디가 더 작은지에 대한 정보를 알고, 더 작은 쪽이 Shift right를 해야하기 때문에 이에 대한 정보를 두 개의 MUX에 보낸다.
• Step 2. big ALU를 통해 fraction의 두 개의 값을 더하고 normalize를 위한 정보를 Control에 전송한다.
• Step 3. 이전 단계에서 얻은 정보로 Shift left or right에서 둘 중 하나를 수행한다.
  그리고 exponent가 더 큰 것을 기준으로 덧셈했기 때문에 큰 것을 기준으로 exponent를 얼마나 줄이거나 키울지 알 수 있다. 이를 Increment or decrement에서 수행한다.
• Step 4. 특정 기준으로 round를 수행하고 4 digit이 되지 않았다면 한 번더 shift left or right와 Increment or decrement를 수행한다.

곱셈은 간단하게 Big ALU를 곱셈으로 바꾸어주면 된다. 하드웨어는 더 복잡하다.
두 덧셈, 곱셈 연산기 모두 integer로 변환할 수 있어야 하고 pipeline도 지원한다.

FP instructions in MIPS

FP 하드웨어는 CPU와 떨어진 coprocessor 1을 사용한다.(exception 처리는 coprocessor 0을 사용한다.)
$f0~ $f1까지의 32bit 레지스터를 사용하며 Double precision은 두 개의 레지스터를 엮어서 사용한다.

• lwc1: load word coprocessor 1
• swc1: load word coprocessor 1
  ldc1, sdc1

single precision
add.s, sub.s, mul.s, div.s
double precision
add.d, sub.d, mul.d, div.d
comparision
c.xx.s, c.xx.d (xx is eq, lt, le, ...)
e.g. c.lt.s $f3, $f4: 결과값을 one bit에 저장해야함. double precision도 있으니 int처럼 한 사이클로 처리할 수 없고, 예외 존재(NaN), 게다가 one bit을 레지스터에 저장하는게 비효율적임
branch
bc1t, bc1f: branch coprocessor 1 when true or false
e.g. bc1t TargetLabel.

FP instruction은 상수를 메모리에 무조건 저장해야한다. 32bit에 명령어와 함께 상수를 담을 수 없음