📆 2022년 9월 20일
하노이의 탑

'하노이의 탑'은 (Tower of Hanoi) 프랑스의 수학자 에두아르 뤼카가 1883년 소개한 문제이다. '작은 원반 위에 큰 원반을 올릴 수 없다'는 규칙을 가지고 있는데, 알고리즘으로는 재귀함수의 좋은 예제가 된다.
📍 규칙
- 한 번에 하나씩 이동해야 한다.
- 작은 원반 위에 큰 원반을 올릴 수 없다.
⇒ 보통 이 조건에서 ‘최소 이동횟수’를 구하거나, ‘최소의 이동횟수로 옮길 때 원반을 옮기는 순서’ 등을 구하는 것이 하노이의 탑 문제로 나온다고 한다.
결론적으로
n개의 원판을 다른 쪽으로 옮기는 데 걸리는 최소 횟수는2ⁿ-1이다.
재귀적으로 접근하는 것이 어려워서 가장 작은 단위로 접근해 본다. 원판 1개가 있을 경우 현재 기둥에서 목적 기둥으로 옮기면 된다. 만약 원판이 2개이 주어진다면?
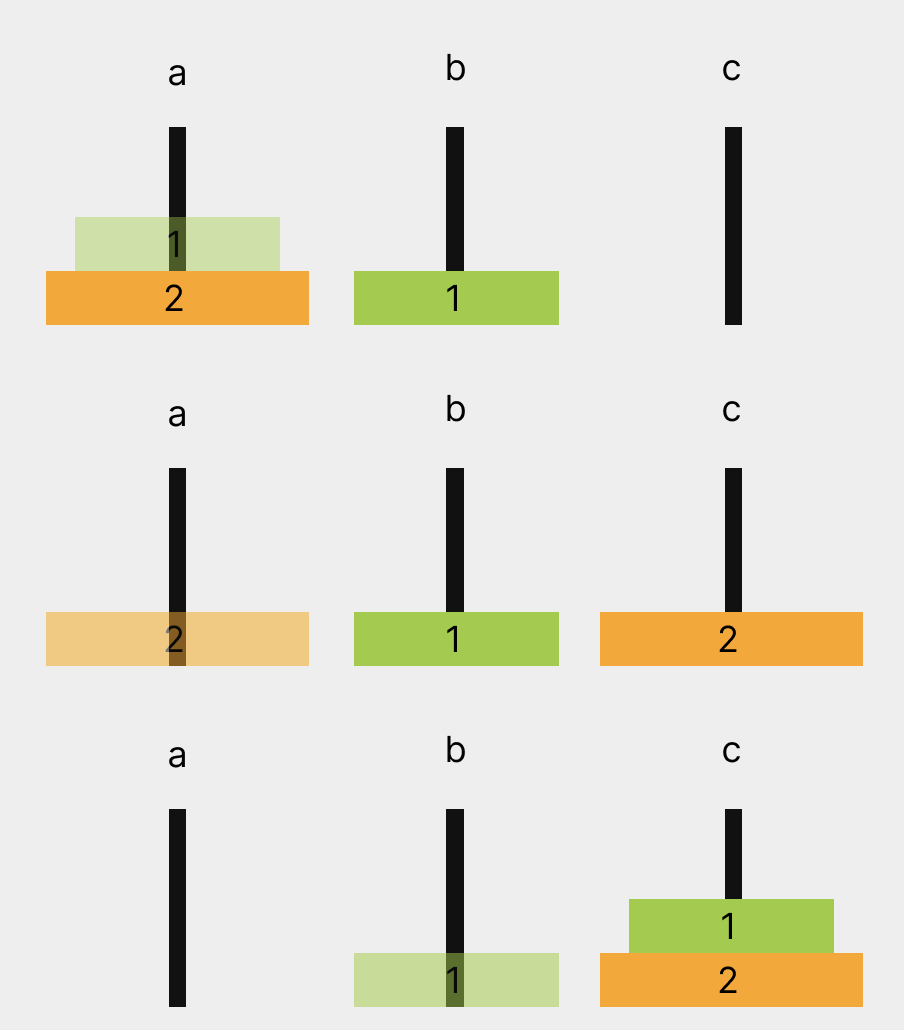
- N개의 원판 중 N-1의 원판을
a기둥에서b기둥으로 옮기고- 남은 하나의 원판은
a기둥에서c기둥으로 옮긴다.- 먼저 옮겼던 N-1의 원판을
b기둥에서a기둥으로 옮긴다.
구현
유명한 문제이기도 하고 잘 알려진 재귀함수 예제이다보니 금방 찾을 수 있었는데,
생각보다 이해하기가 쉽지 않다. 🤔

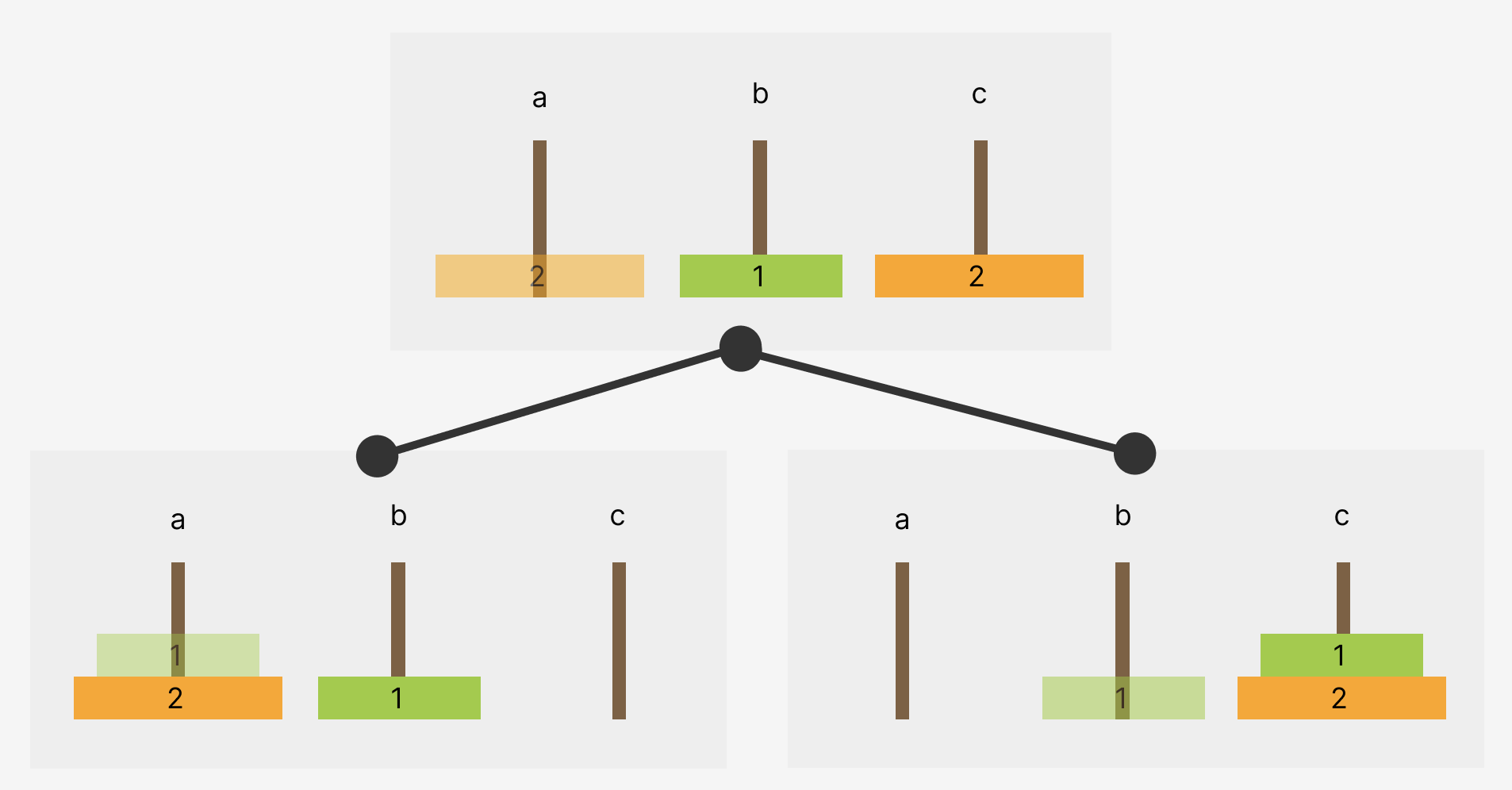
출력문 3번째 줄까지 위 그림과 같은 규칙을 가지고 구현되는 것을 볼 수 있다.
n은 원판의 갯수로 1번보다 작은 원판은 없으니까 num === 0 은 base case가 되겠다.
코드 (javascript)
let count = 0
const hanoi = (num, from, to, sub) => { // 원판갯수, 출발, 목적, 보조
if (num === 0) return
hanoi (num - 1, from, sub, to)
console.log(`${num}번 원판을 ${from}번에서 ${to}로 옮긴다.`)
count++
hanoi (num - 1, sub, to, from)
return count
}
hanoi(3, 'a', 'b', 'c') // 2^3-1 ==> 7
코드 (python)
파이썬 코드 출처는 나무위키
def hanoi(frm, to, n):
if n == 1:
print(f'{frm} {to}')
else:
empty = 6 - frm - to
hanoi(frm, empty, n - 1)
print(f'{frm} {to}')
hanoi(empty, to, n - 1)
print('원반의 개수: ')
numberOfDisk = int(input())
print('원반들의 시작 위치: ')
startLocation = int(input())
print('옮겨야 할 위치: ')
desLocation = int(input())
print('\n')
hanoi(startLocation, desLocation, numberOfDisk)알고리즘 문제
function solution(n) {
let result = []
const hanoi = (num, from, to, other) => {
if (num === 0) return
hanoi(num - 1, from, other, to)
result.push([from, to])
hanoi(num - 1, other, to, from )
return result
}
return hanoi(n, 1, 3, 2)
}다른 풀이
function solution (n) {
const hanoi = (num, from, to, other) => {
if (num === 1) return [[from, to]];
return [
...hanoi(num - 1, from, other, to),
...hanoi(1, from, to, other),
...hanoi(num - 1, other, to, from),
]
}
return hanoi(n, 1, 3, 2)
}const input = require('fs')
.readFileSync('/dev/stdin')
.toString()
.trim()
let result = []
const hanoi = (num, from, sub, to) => { // 원판갯수, 출발, 보조, 목적
if (num === 0) return
hanoi(num - 1, from, to, sub)
result.push([from, to])
hanoi(num - 1, sub, from, to)
return result
}
result = hanoi(+input, 1, 2, 3)
console.log(result.length)
console.log(result.map(el => el.join(' ')).join('\n'))
