Auto-Encoding Variational Bayes 논문 리뷰

오늘은 생성 모델 분야에서 가장 유명한 논문중 하나인 'Auto-Encoding Variational Bayes'를 리뷰해보겠습니다. 사실 해당 논문은 너무 유명하여 질 좋은 리뷰들이 많아 안쓰려고 했지만 쉽지 않은 논문인 만큼 리뷰를 안하고 넘어가면 제가 이해하지 못할 것 같아 작성합니다. 또한 본 논문 리뷰는 독자들께서 베이시안 추론 등 기본적인 통계지식을 갖고있다는 가정아래 작성되었습니다. 마지막으로 저의 주관을 최소화 하려 하기는 하지만 리뷰 특성상 제가 이해한 바로 작성되오니 틀리거나 논의하고싶으실 내용은 언제나! 정말 언제나! 댓글이나 rnrnfjwl11@naver.com 로 연락 주시면 감사드리겠습니다.

1. Introduction

해당 파트에서는 잠재 변수 (latent variables)가 존재하는 경우에 사후 확률 분포 (posterior) 를 추정하는 것은 계산하기 어렵다고 (intractable) 말을 합니다. 물론 모든 경우에서 계산하지 못하지는 않겠지만 만약 사전 확률 분포(prior), 우도 확률 분포 (likelihood)들이 복잡한 형태로 이루어져 있으면 이는 당연시 됩니다. 물론 evidence 또한 계산하기 힘든 경우가 대다수이니 대부분의 경우에서 사후 확률 분포는 intractable하다고 할수 있다고 생각합니다.

이러한 특성으로 인해 ELBO (Evidence of lower bound)를 최대화하는 것은 사후 확률 분포를 근사하는 방법중 하나인데, 본 논문에서는 이를 위한 eastimator, SGVB (Stochastic Gradien Variational Bayes)를 제안했다고 합니다. 또한 데이터가 i.i.d (Independent and Identically Distributed)인 경우, 각 데이터 마다 잠재 변수를 갖게 되고 기존의 방법론들로는 (논문에서는 MCMC가 언급되었네요.) 이러한 잠재변수들에 대한 각 데이터의 사후 확률 분포를 추론해 mean field approach를 통해 최종 사후 확률 분포를 추론해야하기 때문에 expensive iteration이 필요하다고 합니다. 따라서 본 논문에서는 이를 해결해 효율적인 추론을 가능케하는 AEVB (Auto-Encoding VB) algorithm을 제안한다고 합니다.

2. Method

본 논문에서 접근하는 문제들에 대해 다음과 같은 몇가지 가정을 하고 있습니다.

• 모든 데이터 셋은 i.i.d라 가정합니다.
• (Global) parameter에 대해서 maximum likelihood (ML)이나 Maximum a posteriori (MAP)를 진행합니다. -> 이부분이 저는 조금 헷갈립니다만 저는 $p_{\theta}(x)$를 구하기 위해 진행하는 것이라 이해하였습니다.
• latent variables에 대해 variational inference를 진행합니다. -> true posterior $p_{\theta}(z|x)$를 구하기 힘드니 이를 근사하는 $q_{\phi}(z|x)$를 구할 것입니다. (Variational inference란 따로 공부하시기를 권장하오나 간단하게 복잡하거나 intractable한 분포를 직접 구하기 보다 근사하는 다른 분포를 사용해 나타내는 것을 의미합니다.)
• 시나리오를 directed graphical model로 나타내면 다음 그림과 같습니다.

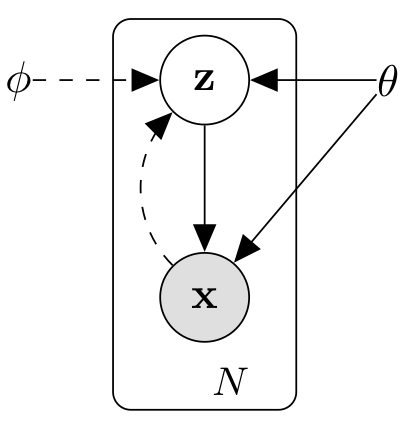
본 그림에서 실선은 generative model을 의미하며 점선은 posterior $p_{\theta}(z|x)$를 varaiational inference하기 위한 근사 분포 $q_{\phi}(z|x)$를 의미합니다.

2.1 Problem scenario

앞에서도 언급했듯이 데이터셋 $X = \{x^{(i)}\}^{N}_{i}$의 형태로 표기되며 i.i.d 조건을 만족합니다. 또한 데이터는 관찰되지 않은 random 연속 변수 z에 의해 다음과 같은 과정으로 생성됩니다.

1. $z^{(i)}$는 prior distribution $p_{\theta^{*}}(z)$에 의해 생성됩니다. ($*$는 true distribution, 즉 해당 변수 분포의 정답 분포를 의미합니다.)
2. $x^{(i)}$가 conditional distriobution $p_{\theta^{*}}(x|z)$로 부터 생성됩니다.
3. $p_{\theta}(z), p_{\theta}(x|z)$는 각각의 true distribution의 family distribution (종류가 같은 분포라는 뜻)이며 모든 $\theta, z$에 대해서 미분 가능합니다 -> $z$가 연속 변수라는 조건과과 함께 각 변수들에 미분이 필요한 SGA (Stochastic Gradient Ascent)를 통해 분포를 추정하기 위함이라 이해했습니다.

또한 본 논문은 위와같은 시나리오 상에서 다음과 같이 3가지 문제를 해결하는데 주안점을 두고 있습니다.

1. ML이나 MAP를 효과적으로 근사한다. -> 앞서 말씀드린 것 처럼 여기서 언급된 ML, MAP가 $p_{\theta}(z|x)$와 $p_{\theta}(x) = p(x|\theta)$ 중 어떠한 posterior 근사하기위해 수행되는 것인지는 아직까지 좀 헷갈립니다만 ELBO를 통해 근사할 수 있는 것은 결국 $p_{\theta}(x)$임으로 저는 해당 분포를 근사하기위해 ML이나 MAP를 수행하는 것으로 이해하였습니다.
2. True poterior ($p_{\theta}(z|x)$)를 근사한다.
3. $x$에 대한 marinal inference를 근사한다. 즉, $p_{\theta}(x)$를 근사한다는 의미입니다.

또한 $p_{\theta}(z|x)$의 근사 분포인 $q_{\pi}(z|x)$는 $x$로 부터 $z$를 생성하기에 reconition model 즉 encoder라 칭하며 반대로 $p_{\theta}(z|x)$는 $z$로 부터 $x$를 생성해내기에 decoder라 칭합니다.

2.2 Varaitional bound

이제 아마 많이들 공부하셨을 ELBO가 등장합니다. 해당식을 본 포스팅에서 유도하지는 않겠지만 한번씩들 스스로 유도해보기를 추천합니다! i.i.d 상황에서 $x$에 대한 marginal likelihood는 다음과 같이 표현될 수 있습니다.

• $p_{\theta}(X) = \Pi_{i}^{N} p_{\theta}(x^{(i)})$
• $log p_{\theta}(x^{(1)},\cdots,x^{(N)})=\sum_{i}^{N}log p_{\theta}(x^{(i)})$

또한 각각의 dataset point $i$에 대한 marginal likelihood는 다음과 같이 표현될 수 있습니다.

• $logp_{\theta}(x^{(i)})=D_{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z|x^{(i)}))+\mathcal{L}(\theta,\phi;x^{i})$

$D_{KL}$은 KL-divergence를 $\mathcal{L}$은 ELBO를 나타냅니다. 이때 KL-divergence 텀은 항상 0보다 크거나 같기때문에 다음과 같은 식이 성립하게 됩니다.

• $log p_{\theta}(x^{(i)}) \geq \mathcal{L}(\theta,\phi;x^{(i)}) = \mathbb{E}_{q_{\phi}(z|x)}[-log q_{\phi}(z|x) + log p_{\theta} (x, z)]$

즉, ELBO를 최대화함으로써 간접적으로 $D_{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z|x^{(i)}))$를 최소화하거나 $log p_{\theta}(x^{(i)})$를 최대화하는 파라미터들을 학습할 수 있다고 생각합니다. 다만 ELBO와 marginal likelihood 모두 $\theta$를 포함하므로 저는 해당 ELBO를 최대화 하는게 앞서말한 역할들을 수행하는데 있어서 최적화된 파라미터들을 찾을 수 있을지는 약간 의문이 드네요... 또한 ELBO는 다음과 같이 변형되어 표현될 수 있습니다.

• $\mathcal{L}(\theta,\phi;x^{(i)}) = \mathbb{E}_{q_{\phi}(z|x)}[-log q_{\phi}(z|x) + log p_{\theta} (x, z)]$
• $\mathcal{L}(\theta,\phi;x^{(i)}) = \mathbb{E}_{q_{\phi}(z|x)}[-log q_{\phi}(z|x) + log p_{\theta} (x^{(i)}|z)+logp_{\theta} (z)]$
• $\mathcal{L}(\theta,\phi;x^{(i)}) = -D_{KL}(log q_{\phi}(z|x)||logp_{\theta} (z)) +\mathbb{E}_{q_{\phi}(z|x)}[log p_{\theta} (x^{(i)}|z)]$

이러한 ELBO를 계산하기 위해 다양한 eastimator (예를들어 Monte Carlo gradient estimator)가 사용되어왔지만 매우 큰 high variance를 가진다고하네요. 결국 본 논문의 가장 주된 목적은 variance가 작은 ELBO eastimator를 제안하는 것이라는 생각이 듭니다.

또한 위 가장 마지막식을 보면 KL-divergence는 posterior $p(z|x)$가 prior $p(z)$와 유사하게 학습되는 경우 ELBO 값이 커진다는 걸 알 수 있습니다. 즉 해당 텀은 $p(z|x)$의 표현력을 어느정도 제한한 다는 점에서 regularizer 역할을 합니다 (정확히 이해하기 위해서는 더 공부를 해봐야 겠지만 encoder의 목적은 주어진 데이터 $x$를 의미있는 임베딩 $z$으로 만드는 것이라는 의미에서 $z$가 너무 광범위한 범위를 갖도록 학습하는걸 제한한다고 생각합니다). 또한 두번째 텀은 $p(x|z)$가 커져야 하는데 이는 $z$로부터 생성된 데이터 $x$가 존재할 만한 데이터로 만들어주는 reconstuction 텀입니다. 여러모로 ELBO를 최대화하도록 학습하는 것이 왜 generative model의 objective가 되는지 알 것 같습니다.

2.4 The reprametrization trick

(2.3) section을 이해하기 위해서는 본 section의 내용을 선행적으로 이해해야 한다고 판단해서 순서를 조금 바꿨습니다. 양해 부탁드립니다. (2.3)에서 다루겠지만 본 논문에서는 ELBO를 eastimation하기 위해 $x$로 부터 $z$를 생성하하고 $z$로 부터 다시 $x$를 생성하는 ancentral 방법을 사용하게됩니다. 이때 $z$를 샘플링하는 $z$ ~ $q_{\phi }(z|x)$ 과정에서 아주 큰 문제를 직면하게 됩니다. 바로 샘플링된 $z$는 determistic하지 않기 때문에 학습 학습 파라미터들을 기준으로 미분을 취할 수 없게 됩니다. 따라서 $z=g_{\phi}(\epsilon, x)$, $\epsilon$ ~$p(\epsilon)$을 통해 $z$를 determistic한 variables로 표현하며 이를 reprametrization trick이라 칭합니다. 이때 $g_{\phi}$는 $\epsilon$을 $z$로 변환시켜는 transformation function을 의미합니다.

이해하기 어려울 것 같아 간단한 예를 보여드리겠습니다. 만약 $z$ ~$q_{\phi}(z|x)=\mathcal{N}(\mu, \sigma^{2})$라고 한다면 sampling된 $z$에 대해서 $\phi$를 기준으로 미분할 수가 없습니다. 그러나 $\epsilon$~$\mathcal{N}(0,1)$일 때, $z=\mu+\sigma \epsilon = g_{\phi}(\epsilon, x)$가 성립하기 때문에 $\phi$를 기준으로 미분가능하게 됩니다. 물론 적절한 미분가능한 transformation function을 선택할 수 있어야 되겠죠! 본 논문에서는 이를 위해 세가지 간단한 접근법들을 제안합니다만 해당 부분은 죄송하게도 제 이해밖입니다... :(

2.3 The SGVB eastimator and AEVB algorithm

(2.4)에서 다룬 것처럼 적절한 transformation function을 찾을 수 있고 reparametrization trick을 적용할 수 있는 경우에 다음과 같은 Monte Carlo eastimation을 적용할 수 있습니다.

• $\mathbb{E}_{q_{\phi}(z|x^{(i)})}[f(z)] = \mathbb{E}_{p(\epsilon)}[f(g_{\phi}(\epsilon, x^{(i)}))] \simeq{{1}\over{L}}\sum_{l}^{L}f(g_{\phi}(\epsilon^{(l)}, x^{(i)})) \; where \; \epsilon^{(l)} \sim p(\epsilon)$

따라서 $\mathcal{L}(\theta,\phi;x^{(i)}) = \mathbb{E}_{q_{\phi}(z|x)}[-log q_{\phi}(z|x) + log p_{\theta} (x, z)]$ 식은 다음과 같이 sampling된 $z$들에 의해 근사될 수 있으며 이러한 eastimator를 Stochastic Graident Variational Bayes (SGVB) eastimator의 첫번째 버전 $\mathcal{L}^{A}(\theta,\phi;x^{(i)})$입니다.

• $\mathcal{L}^{A}(\theta,\phi;x^{(i)})={{1}\over{L}}\sum_{l}^{L} [log p_{\theta} (x^{(i)}, z^{(i,l)}) -log q_{\phi}(z^{(i,l)}|x^{(i)})]\;where\;z^{(i,l)} = g_{\phi}(\epsilon^{(i,l)}, x^{(i)}) \; and \; \epsilon^{(l)}\sim p(\epsilon)$

해당 식에서 학습 파라미터들 $\theta, \phi$에 대해서 모두 미분 가능하기 때문에 gradient ascent 방법으로 점점 최대화 될 수 있습니다.

또한 ELBO를 다르게 표현한 $\mathcal{L}(\theta,\phi;x^{(i)}) = -D_{KL}(log q_{\phi}(z|x)||logp_{\theta} (z)) +\mathbb{E}_{q_{\phi}(z|x)}[log p_{\theta} (x^{(i)}|z)]$ 식에서 KL-diveregence 텀이 충분히 계산가능하다면 최소한의 샘플링과 monte carlo eastimation을 적용하여 다음과 같이 두번째 버전의 SGVB, $\mathcal{L}^{B}(\theta,\phi;x^{(i)})$를 계산해낼 수 있습니다.

• $\mathcal{L}^{B}(\theta,\phi;x^{(i)}) = -D_{KL}(log q_{\phi}(z|x^{(i)})||logp_{\theta} (z)) +{{1}\over{L}}\sum_{l}^{L}\log p_{\theta} (x^{(i)}|z^{(i,l)})\;where\;z^{(i,l)} = g_{\phi}(\epsilon^{(i,l)}, x^{(i)}) \; and \; \epsilon^{(l)}\sim p(\epsilon)$

또한 KL-divergence의 계산 예시는 제한된 가우시안 분포에 한해 (Appendix B)에 기재되어 있으므로 참고해주시길 바랍니다. 이 두번째 버전은 하나의 텀이직접 계산되었기 때문에 좀 더 적은 variance를 가진다 할 수 있을 것 같습니다.

또한 최종적으로 $N$개의 데이터 갯수를 갖는 ELBO는 M개의 배치 데이터셋을 통해 다음과 같이 추정될 수 있습니다.

$\mathcal{L}^{B}(\theta,\phi;X) = \mathcal{L}^{M}(\theta,\phi;X^{M})={{N}\over{M}}\sum_{i}^{M}\mathcal{L}^{AorB}(\theta,\phi;x^{(i)})$

다만 $L$이 충분히 커야 ELBO를 좀 더 잘 근사할 것이라 생각했는데 실험에서는 $L$을 1으로 $M$을 100으로 설정하였다고 하네요.

이러한 SGVB eatimator를 활용해서 ELBO를 maximization하는 알고리즘을 Auto-Encoding VB (AEVB) algorithm을 이라하며 다음과 같은 과정을 통해 학습됩니다.

3. Example: Variational Auto-Encoder

본 section에서는 variation auto-encoder를 실제로 적용하는 예시를 보여줍니다. 이를 위해 아래와 같은 몇가지 가정을 하게됩니다.

• $p_{\theta}(z) = \mathcal{N}(z;\mathbf{O}, \mathbf{I})$인 multivariate gaussian으로 가정합니다.
• $p_{\theta}(x|z)$는 Mutilvariate gaoussian 혹은 bernoulli 분포라 가정합니다.
• $p_{\theta}(z|x)$는 intractable하지만 diagonal covariance를 갖는 multivariate gaussian 혹은 bernoulli분포로 가정하기 때문에 $q_{\phi}(z|x)$ 또한 같은 형태의 분포를 띈다고 가정합니다.
• $\epsilon^{(l)}\sim \mathcal{N}(z;\mathbf{O}, \mathbf{I})$

이러한 상황에서 $\mathcal{L}^{B}(\theta,\phi;x^{(i)}) = -D_{KL}(log q_{\phi}(z|x^{(i)})||logp_{\theta} (z)) +{{1}\over{L}}\sum_{l}^{L}\log p_{\theta} (x^{(i)}|z^{(i,l)})$를 최적화하는 과정은 다음과 같습니다.

1. $z$를 샘플링 하는 과정
   $x^{(i)}$를 input으로 하는 $MLP_{\phi}$의 ouput과 $\epsilon$의 샘플링을 통해 진행됩니다. 예를들어 논문에서는 정확하게 명시되어 있지는 않지만 $\mu^{(i)}=f(W_{\phi, \mu}*x^{(i)}+b_{\phi, \mu}), \sigma^{i}=f(W_{\phi, \sigma}*x^{(i)}+b_{\phi, \sigma})$ 연산에 의해 계산될 수 있고 $\epsilon$을 샘플링 한 후, determistic한 $z^{(i,l)}=\mu^{(i)}+\sigma^{(i)}\odot \epsilon^{(l)}$를 계산할 수 있습니다.
2. $D_{KL}(log q_{\phi}(z|x^{(i)})||logp_{\theta} (z))$ 계산
   (Appendix B)에 수식적으로 계산하는 것이 상세히 나와 있습니다. 앞서말한 조건들에서는 KL-divergence 값은 ${{1}\over{2}}\sum_{j}^{J}(1+log((\sigma_{j}^{(i)})^{2})-(\mu_{j}^{(i)})^{2}-(\sigma_{j}^{i})^{2})$입니다. $j$는 $\mu, \sigma$ 벡터들의 각 차원입니다. 이로써 $\mathcal{L}^{B}$의 왼쪽 텀이 계산이 되었네요!
3. $log p_{\theta} (x^{(i)}|z^{(i,l)})$ 계산
   (Appendix C)에 보다 자세히 나와있습니다. 이역시 관찰된 $z^{(i,l)}$들을 입력으로 하여 $MLP_{\theta}$의 output을 통해 계산할 수 있습니다.
   

이후에는 AEVB 알고리즘을 통해 반복적으로 학습해주시면 됩니다! 오로지 analytic한 계산을 통해 구하는 full VB나 $\mathcal{L}^{A}$를 통해 최적화하는 방법도 Appendix에 있으니 그냥 쓱 훑고 지나가는 것이 좋을 것 같습니다. 초창기 모델이기도 하여 해당 모델을 선택하여 사용하는 경우도 드물뿐 아니라 아 이런식으로 계산할 수 있구나 하면되지 직접 계산하는 경우는 많지 않을 것 같습니다.

4. Related work

본 분야에 대한 지식이 부족하여 과감히 생략. Generative model을 좀 더 공부하고 이전 연구들에 대한 공부가 필요할 때 좀 더 학습하여 이해가능하게 적어볼 수 있도록 하겠습니다!

5. Experiments

실험을 크게 3개가지 정도로 진행되었다.

1. Lower bound의 크기 비교
   앞서 언급했듯이 일차적으로 lower bound의 값이 커야 generative model이 잘 학습되었다고 말할 수 있습니다. 그런의미에서 진행한 실험이고 다음 사진과 같은 결과를 확인할 수 있습니다. 워낙 짧게 언급이 되어 저도 자세히는 다루지 않겠습니다.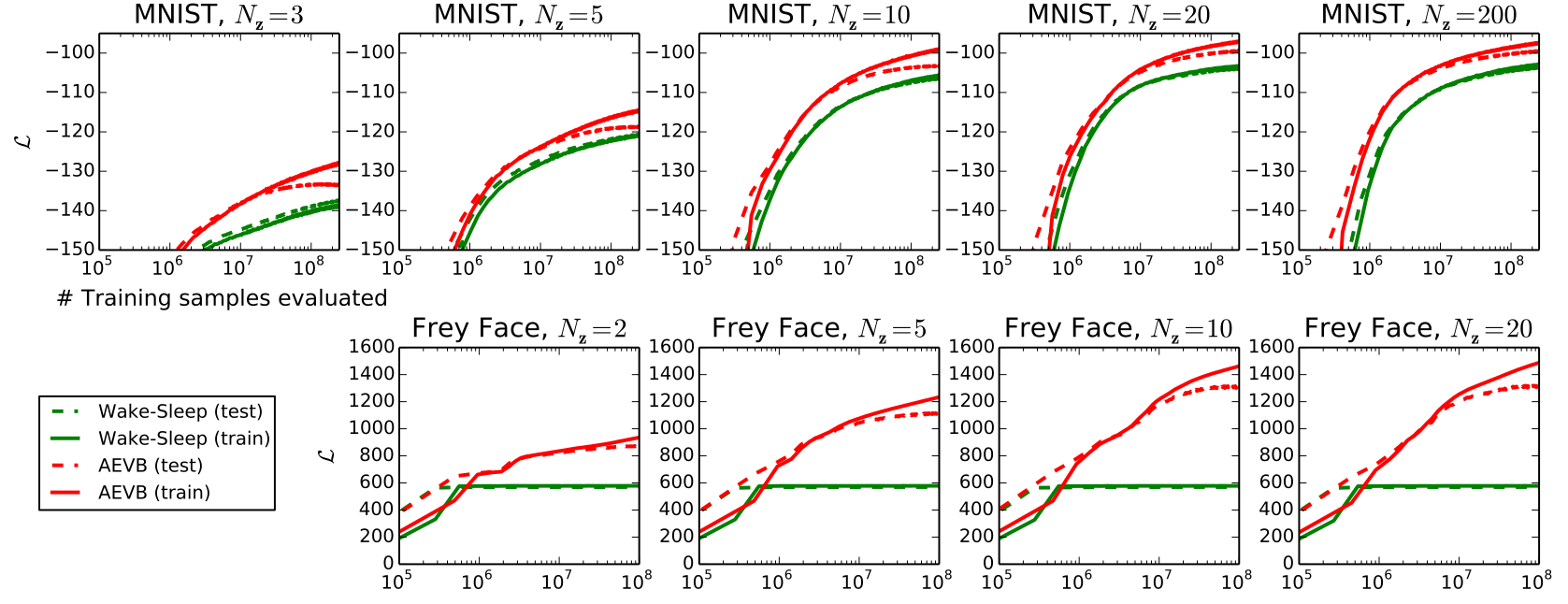

   

2. Marginal likelihood $(p(x))$의 크기 비교
   ELBO를 최대화하도록 학습하는 것이 생성 모델의 목표인것 전에 ELBO를 최대화 하는 것은 Marginal likelihood $(p(x))$를 최대화하는 것이었습니다. 즉, Marginal likelihood 값이 크다면 좋은 생성 모델이라고 할 수 있겠지요. 이를위한 실험이고 결과는 아래와 같습니다.

   

3. 생성 이미지 시각화
   당연히 이미지 시각화도 진행을 했습니다. 절차는 $p(z)$로 부터 inverse CDF sampling을 통해 $z$를 sampling하고 $p(x|z)$에서 $x$를 샘플링해 생성해내지 않았을 까 싶습니다. 결과는 아래와 같습니다.

   

마치며

드디어 끝났습니다. 본 포스팅에서는 VAE 가장 초창기 모델에 대한 논문을 리뷰해보았는데 아무래도 초창기 논문이다보니 활용보다는 기본적인 수식들을 전개하는데 집중했던 것 같습니다. 본 포스팅을 시작으로 GAN과 요즘 핫한 diffusion model까지 다양한 생성 모델을 포스팅해볼까 합니다. 앞으로 열심히 해야겠네요... ㅎ. 질문이나 틀른 것 같이 논의해볼만한 것에 대한 답변은 언제나 환영입니다. 사실 환영 수준이 아니고 많이 고파있기도 하고 읽어주신 분들도 같이 생각해보면 무조건 적으로 좋은 것이니 댓글이나 메일을 통한 연락 꼭 부탁드립니다!