1. Introduction
개인적으로 읽어왔던 논문들 중에서 가장 명쾌하고 재미있는 인트로였습니다. 초반부분은 discriminative model들에 비해 generative model들은 비교적 덜 발전을 이루어왔다 언급합니다. 따라서 본 논문은 좋은 generative model을 학습하기 위해 adversarial nets framework를 제안합니다.
Adversarial nets는 discriminative model과 generative model로 구성되는데 본 논문은 이러한 framework를 다음과 같은 게임에 비유하여 설명하고 있습니다. Generative model은 위조 지폐를 생산해내고 discriminative model은 해당 지폐가 위조인지 아닌지 구분해내야 합니다. 이러한 방식의 학습을 통해 generative model은 점점 더 진짜 같은 위조 지폐를 만들 어내고 discriminative 모델의 구별 능력 또한 점점 높아지게 됩니다. 이러한 상호적인 학습은 통해 두 모델 모두 자신이 수행해야하는 task를 점점 잘 하게 되는 것이지요.
2. Rlated work
Boltzman Machine이나 Deep belief networks 등을 잘 알지 못해 패스하겠습니다.. 이해가 어렵네요 ㅠ
3. Adversarial nets
Generator는 앞서 말쓴 드린 것 처럼 노이즈 ()를 인풋으로 받아 데이터를 생성해내는 모델 입니다. Generator에 사용되는 notation들은 다음과 같습니다.
- 는 generator가 생성해내는 데이터의 분포를 의미합니다.
- Input noise의 prior는 로 표기합니다.
- Generator는 로 표기하며 MLP입니다. 즉, Generator는 를 input으로 받아 를 학습 변수로 하여 이미지를 생성해내는 MLP입니다.
Discriminator는 데이터의 위조 여부를 판변해주는 모델이며 notation들은 다음과 같습니다.
- 모델은 로 표기합니다. 이는 data 가 가 아닌 real data에서 왔을 확률을 의미하며 는 학습 모델의 학습 파라미터를 의미합니다.
이러한 generator와 discriminator는 다음과 같은 과정을 통해 학습됩니다.
- Discriminator 는 위 전체 식이 최대화 되도록 학습합니다. 이는Discriminator가 로 부터온 real data는 진짜 데이터로 로 부터 생성되는 데이터는 가짜 데이터로 분류하도록 학습됩니다.
- Generator는 식이 최소화 되도록 학습됩니다. 이는 discriminator가 진짜, 가짜를 구분하기 어렵도록 가 진짜 같은 데이터를 생성하도록 학습합니다.
이러한 과정은 반복적으로 이루어집니다. 저자는 만약 가 iner loop에서 학습될 경우 (그냥 와 반복적으로 학습되지 않을 경우) 몇몇의 data에 대해서 오버피팅이 이루어진다고 합니다. 따라서 discriminator를 몇 스텝 학습하고 generator를 학습하는 과정을 반복적으로 수행해 optimal solution에 도달하도록 합니다. 저자는 이학습 과정을 아래와 같은 figure를 통해 설명합니다.
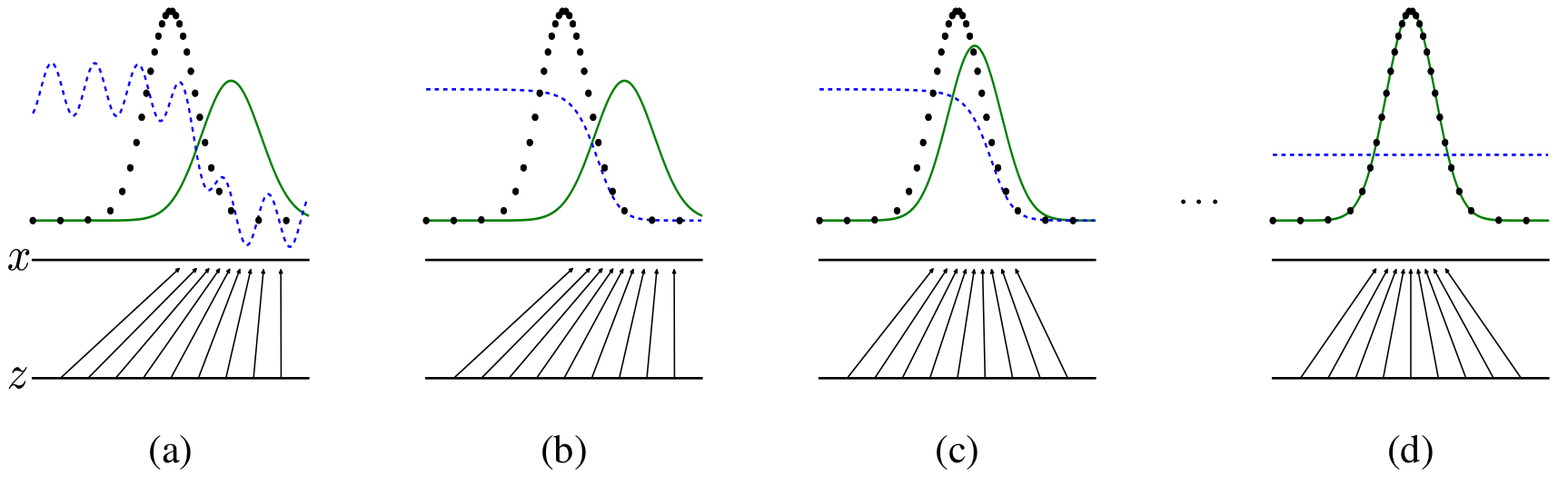
위 그림에서
- 검은색 선은 real data의 분포를 나타냅니다. 파란선은 discriminator의 분포 (각 데이터가 real data에서 나왔을 것음 예측하는 확률에 대한)를 나타냅니다. 초록색선은 generator가 만들어내는 data의 분포를 나타냅니다.
- 는 각 real data의 data point를 와 화살표는 noise 가 generator 로 인해 real data로 매핑되는 과정을 의미합니다.
- (a)는 generator가 일부 학습되어 real data에 어느정도 유사한 데이터를 생성해내는 것을 나타냅니다.
- (b)는 이러한 generator에 의해 discriminator가 학습된 것을 나타냅니다.
- (c)에서는 좀 더 real data 분포에 맞는 데이터를 생성해내는 generator를 보여줍니다.
- (d)는 완전한 위 과정들이 반복적으로 학습된 후 완전한 optimal solution에 도달한 것을 나타냅니다. (, )
이에대한 알고리즘은 아래와 같은데 별로 이해하기 어렵지는 않으실 겁니다! 저자는 다만 학습 초기에 의 성능이 안좋아 discriminator가 너무 잘 판별해 가 saturation 되니, 를 최소화하는 것보다 가 최대화 되도록 학습한다고 합니다.
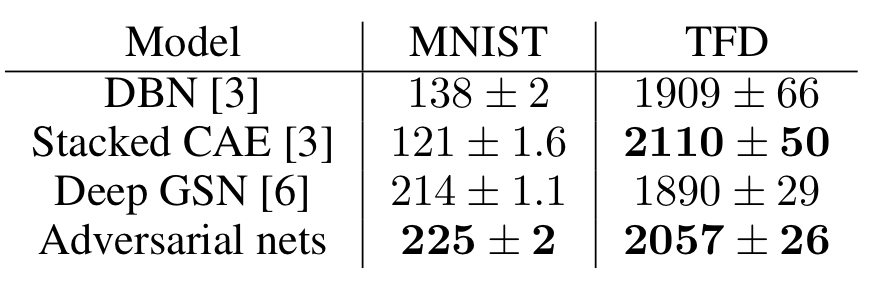
Theoretical Results
4.1 Global Optimality of .
해당 과정에서는 아래와 같이 가 고정되 있다고 가정할 때 optimal discriminator 임을 증명합니다.
이때 는 에서 최댓값을 갖기 때문에 위 식의 인테그랄 내부의 disiciriminator가 일 때 최대화되는 식이 됩니다.
다음 과정에서는 generator model을 학습할 때 가 optimal solution임을 증명합니다.
이후에 Theorem 1에서는 가 위 식을 최소로 하는 G를 학습시키기 위한 optimal solution임을 증명합니다. 저는 해당 증명을 따라가다 보니 수식은 이해가 가는데 전개 과정이 이해가 안갑니다. 를 가정해 놓고 해당 식의 최솟값을 정한 후에 일 때 해당 최솟값이 달성됨을 다시 보여주기 때문입니다...
개인적으로는 인정할 수 없는 증명이었습니다! 저는 해당 과정이 "GAN의 학습은 사실 와 의*Jensen-Shannon divergence를 최소화하는 것이다."라는 결론에 맞추기 위한 작위적은 증명 같습니다...
추가적으로 4.2절의 convergence of algorithm 1에 대해서는 이해하지 못했습니다.
5. Experiments
첫번째 실험은 아래와 같이 생성된 데이터 들의 loglikelihood( ) 비교 실험 입니다. 다만 GAN은 p_{g}을 explicit하게 계산할 수 없기 때문에 parzan window를 사용한 비모수적 추정법을 이용했다고 합니다.
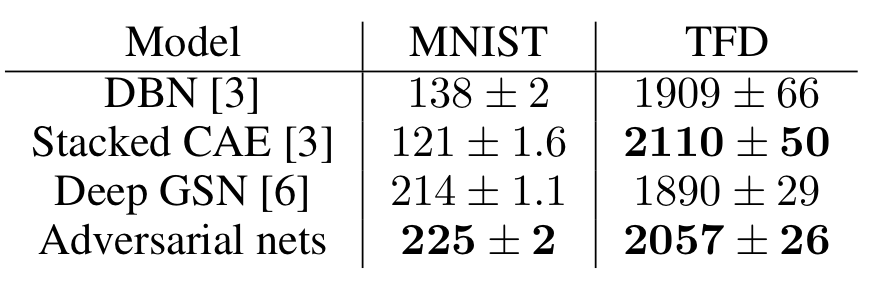
아래는 generator로 부터 생성된 sample들을 나타냅니다.

아래 그림은 space 상에서 linearly interpolating 작업을 통해 추출되고 generator로 생성된 sample들을 나타냅니다.
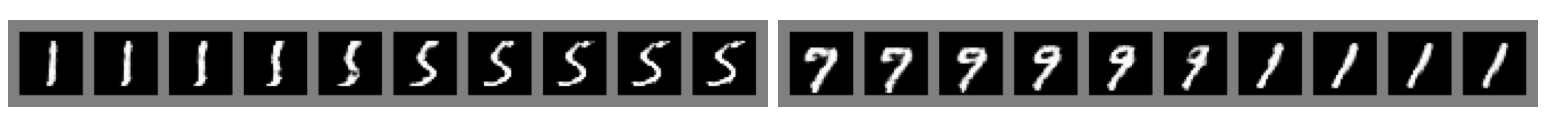
6.Advatages and disadvantages
단점은
- explicit한 를 계산할 수 없다.
- Training 과정이 복잡하고 어렵다.
로 요약될 수 있습니다.
장점은
- 생성된 데이터가 discriminator에 의해 간접적으로 평가되어 학습 되므로 input sample을 카피하지 않는다.
- sharp한 이미지를 생성해 낼 수 있다. (why...?)
정도로 정리가 됩니다.
7. Conclusions and future work
첫번째 future work은 를 explicit하게 계산해 내는 것을 두번째는 , 즉 inference 과정 또한 수행하는 것으로 언급하며 논문을 마무리 합니다.