Inductive Representation Learning on Large Graphs 리뷰

Introduction

논문을 리뷰하기 전에 우선 'Inductive'라는 용어에 대해서 간단히 설명하겠다. 정확한 반대의 의미는 아니지만 해당 용어의 대척점에 있는 용어중 'transductive'라는 용어가 있다. gnn 분야에서 사용 되는 transductive란 input graph 내에서 task를 수행하는 것이다. 예를들어 'Semi-Supervised Classification with Graph Convolutional Networks'에서는 GCN을 제시하고 semi supervised learning을 수행하는데 이는 다음 그림과 같이 이미 label을 아는 노드를 중심으로 gcn 모델의 가중치를 학습 시켜 label을 알지 못하는 노드들에 대해서 node prediction을 진행한다.(해당 그림에서는 학습전엔 $Z_{1}, Z_{2}$의 경우는 label을 알고 있고 나머지 노드는 라벨을 알지 못한다.) 이경우 새로운 input 그래프에서 task를 수행하기 위에서는 재학습이 필요하며, 가중치 행렬의 모양이 고정되어 있기 때문에 새로운 모양의 graph의 경우 학습이 매우 어려워 진다.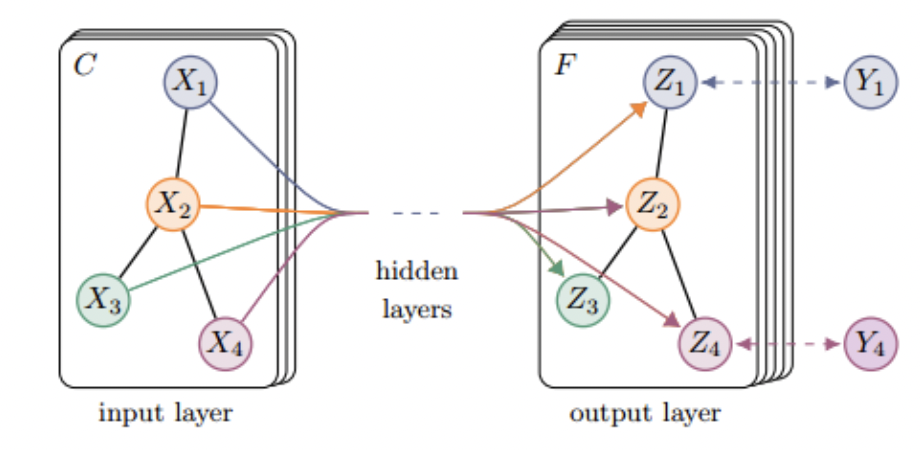
'inductive'란 하나의 instance, 그래프 내에서 task를 수행하는 것이 아니고 여러 input graph에 대해 학습을 진행하는 것이다. 즉 새로운 input graph에 대해서도 이미 학습되어 있는 GNN 모델을 이용해 task를 수행하는 것이 가능하다.

논문의 저자는 기존의 GNN 모델들은 다소 transductive한 성질을 지니고 있으며 실제 모양이 다양한 그래프를 다루기 위해서는 inductive한 GNN 모델이 필요하다. 이러한 이유로 기존의 transductive한 gcn의 일반성을 확장시켜 inductive한 성질을 지닌 GNN 모델을 제시한다.

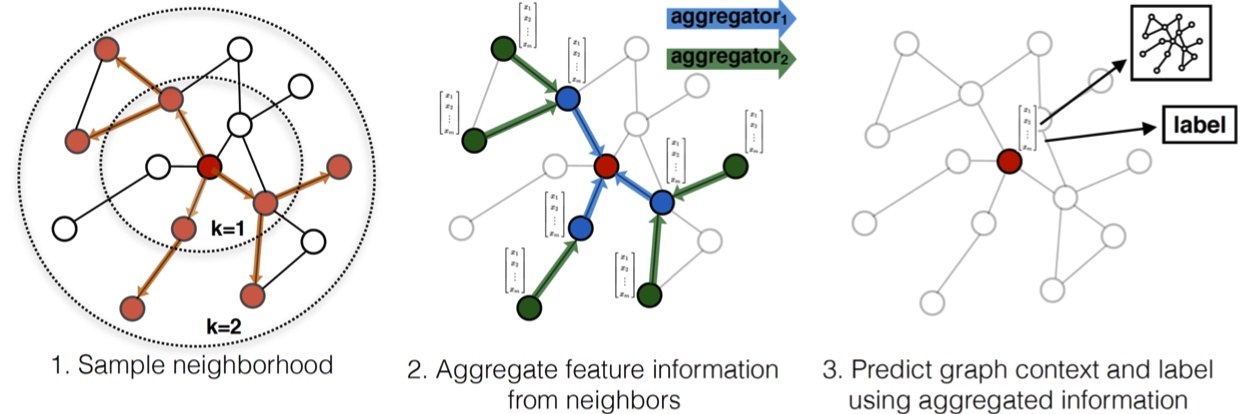
따라서 기존 일반적인 gnn 모델들과 같이 각각의 node 혹은 graph들이 구별될 수 있도록 하는 embedding에 집중하여 학습시키는 방법과는 다르게 그림과 같이 기준 노드를 중심으로 하나이상의 k-hop-aggregator를 학습시켜 노드 주변의 feature들을 집계하고 structure를 파악할 수 있도록 한다.

Related work

과감히 생략

Proposed method: GraphSAGE

Embedding generation algorithm

해달 모델에서는 다음과 같은 노드 임베딩을 수행한다.
위와 같은 알고리즘은 크게

• $AGGREGATE_{k}(\{h_{u}^{k-1}, \forall u \in \mathcal{N}(v)\})$ - $h^{k}_{v}$를 update하기 위해서 기준 노드의 주변 노드들을 집계(aggregate)하는 과정

• $\sigma(W^{k}\cdot CONCAT(h_{v}^{k-1}, h_{\mathcal{N}(v)}^{k}))$ - 주변 노드의 집계로 생성된 벡터($h^{k}_{\mathcal{N}(v)}$)와 전 층의 중심 노드의 벡터($h^{k-1}_{v}$)를 합쳐서 현재 층의 중심 노드의 벡터($h^{k}_{v}$, 각 노드에 대한 최종적인 벡터)를 생성하는 과정

의 두가지 과정으로 이루어지며 사실 각 노드에 대해 새로운 feature vector를 정의하기 위해 Aggregation과 Combine 과정을 진행하는 기존의 gnn 모델과 크게 달라 보이지는 않는다.

Relation to the Weisfeiler-Lehman Isomorphism Test

Weisfeiler-Lehman Isomorphism Test... 참 꾸준히도 나온다... 죄송하지만 이것에 대해서는 아는 것이 없다. 추후에 남는 시간에 꼭 학습하여 여러분들께 전달하도록 하겠습니다. 해당 논문에서는 WL test의 아이디어를 일부 차용했으며 여러가지 조건(K, W, Aggregator F)등을 변경한다면 위와 같이 GraphSAGE에 사용된 알고리즘은 WL test의 Instance로 볼 수 있다고 언급하고 있다.

Neighborhood definition

해당 모델에서는 기준 노드에 대한 주변 노드를 모두 사용하지는 않는다. 대신에 고정된 크기로 샘플링하여 사용한다. 이는 예상컨대 주변 노드의 개수가 계속 바뀌는 경우 이에대한 모델을 동적으로 설계하는 것은 매우 비효율적이며 주변 노드의 개수가 많을 경우 많은 계산 시간이 소요되기 때문일 것이다. 따라서 주변 노드의 갯수를 고정시키면 $O(\prod^{K}_{i=1}S_{i})$의 시간복잡도를 갖게 된다.($S$에 대한 정확한 명시는 없지만 샘플링 사이즈로 예상했다.)

Learning the parameters of GraphSAGEhg

GraphSAGE의 학습을 위해서는 output representation($z_{u}$)를 사용해야 하며 aggregator function의 parameter(무엇을 의미하는지는 솔직히 잘 모르겠다.) 최종적으로 $W_{k}$를 학습하여야 한다. 이러한 학습을 위한 손실 함수는 다음과 같다.

• $J_{\mathcal{G}}(z_{u}) = -\log(\sigma(z^{\top}_{u}z_{v})) - Q \cdot \mathbb{E}_{v_{n}\sim P_{n}(v)} \log(\sigma(-z^{\top}_{u}z_{v}))$

$v =$ 고정된 길이의 random walk에 의해 노드 $u$와 동시 발생하는 노드
$P_{n} =$ negative sampling distribution
$Q =$ negative sample의 갯수

이러한 수식은 각 노드를 unique embedding 시키는 것에 집중하기 보다는 중심 노드가 주변노드와의 관계성에 의해 representation되는 데에 집중한다. 또한 중심 노드를 비슷한 representaion(이부분은 정확히는 모르겠다)을 가지는 노드와의 유사성은 증가시키고 상이한 representation을 가진 노드와는 구별될 수 있도록 학습시킨다.

'embedding algorithm generation' 7번째 줄에서 볼 수 있듯이 해당 모델은 rpesentation 생성시 매 과정에서 정규화를 실시한다. 따라서 $z^{\top}_{u}z_{v}$식은 두 벡터터의 크기로 굳이 나누어지지 않아도 그자체로 코사인 유사도의 의미를 가지고 있다. 시그모이드 함수는 값을 0~1로 맵핑 시켜주므로 $-\log(\sigma(z^{\top}_{u}z_{v}))$는 코사인 유사도가 가장 큰 1일 때 0으로 최솟값을 가지며 유사도가 작아질수록 손실값이 커지는 기준 노드와 다른 노드간의 유사성을 측정할 수 있는 함수이다.

반대로 $- Q \cdot \mathbb{E}_{v_{n}\sim P_{n}(v)} \log(\sigma(-z^{\top}_{u}z_{v}))$는 코사인 유사도에 -기호를 붙여서 코사인유사도가 가장 큰 1일때는 오히려 손실값이 커지게 하고 가장작은 -1일때는 1의 값으로 손실값을 0으로 만들어준다. 이는 기준노드와 representation이 달라야 하는 네거티브 샘플링된 노드에 관하여 distinct를 극대화 시켜주기 위한 함수이다.
(통계나 데이터 샘플링에 관한 지식이 많이 부족하여 왜 기댓값을 취하는지 굳이 네거티브 샘플링의 갯수를 왜 곱해주는지는 아무리 생각해도 알지 못하겠다...)

Aggregator Architecture

그래프의 특성은 structure가 노드간의 연결 관계로 정의 된다는 것이다. 즉 이미지 데이타의 경우 해당 이미지의 픽셀의 좌표 자체가 구조적인 정보를 담고 있지만 그래프의 경우는 그렇지 않다.

즉 그림과 같은 두 그래프는 모양은 달라보일 수 있지만 노드와 노드들 사이의 연결관계가 동일하기 때문에 같은 그래프로 취급할 수 있다. 또한 한 그래프를 Adjacent matrix나 feature matrix로 표현할 때 표기하는 노드의 순서에 의해(위 그림에서는 feature matrix의 row(node)의 순서를 1,2,3...으로 하든 3,2,1...로하든 노드간의 연결성과 특성만 보존하고 있다면 본질 적으로 같은 그래프로 해석하여야 한다.) output에는 전혀 영향이 없어야 한다.
이러한 그래프 데이터의 특성으로 인해 Aggregator function은
노드들의 permutation에 invariant하여야 한다. 따라서 이러한 특성을 유지하는 symmetric한 특성을 지닌 Aggregator를 세가지 제안한다.

1. Mean aggregator
이전 알고리즘의 4(aggregation), 5(combine)과정을 다음과 같은 수식으로 대체한다.

• $h^{k}_{v} \leftarrow \sigma(W \cdot MEAN(\{h^{k-1}_{v}\} \cup \{h^{k-1}_{u}, \forall u \in \mathcal{N}(v)\})$

즉 기준 노드와 주변 노드의 평균값을 이용하여 기준 노드의 새로은 repersentation vector를 updata한다.

2. LSTM aggregator
LSTM은 본디 시계열 데이터를 처리하므로 보통 unsymmetric 하지만 주변 노드를 랜덤한 순서로 반복 학습시킬 경우 LSTM의 unsymmetric한 성질을 완화시킬 수 있다. 또한 LSTM을 활용할 경우 representation vector의 표현 능력이 증가하게 된다.(이부분은 잘이해가 되지 않는다. 도대체 어떤 부분에서 표현 능력이 증가한다는 것인지...)

3. Pooling aggregator
이전 알고리즘의 4(aggregation)과정을 다음과 같은 수식으로 대체한다.

• $AGGREGATE^{pool}_{k} = \max(\{\sigma(W_{pool}h^{k}_{u_{i}} + b), \forall u_{i} \in \mathcal{N}(v)\})$
  

이는 주변 노드들을 single-layer perceptron에 투입하고 그 output에 대해서 element-wise max를 취하여 aggregation을 진행하는 방식이다. 이러한 방식은 single-layer perceptron을 도입으로 인한 새로운 가중치를 사용으로 인해 최종 repregentation vector의 표현력이 증대될 것으로 예상된다. 물론 max는 mean, min등의 symmetric한 operator를 통해 치환될 수 있다.