linear regression (선형회귀)

본 글은 전문적인 관점에서 쓰여진 것이 아닌 순전히 제가 생각하고 배워온 선형 회귀에 대해 작성한 글입니다! 질문이나 같이 의논해볼 사항 또는 글의 오류에 대한 논의는 언제나 환영이니 'rnrnfjwl11@naver.com'으로 메일 보내주시거나 댓글 달아주세요 !

Linear Regression

선형 회귀는 종속변수 ($y$)와 독립변수($x$)쌍으로 이루어진 데이터는 $(x, y)$들이 주어졌을 때 이를 선형식으로 모델링하는 것입니다.

말은 복잡해 보이지만 결국엔 주어진 변수(데이터)들에 맞게 $y=wx+b$ 식의 $w$와 $b$를 찾는 것입니다. 아주 간단한 예제를 보겠습니다. 만약 데이터가 $(2, 3), (3, 4)$으로 주어졌을 때 이에 맞는 선형식을 찾는 방법은 아주 간단합니다. 중학교때 직선의 방정식 배운 것 기억하시나요?! 여기서 굳이 구하는 식은 보여드리지는 않지만 어떠한 방법이든지 활용하셔서 구하면 다음과 같은 선형식을 얻으실 수 있을 겁니다.

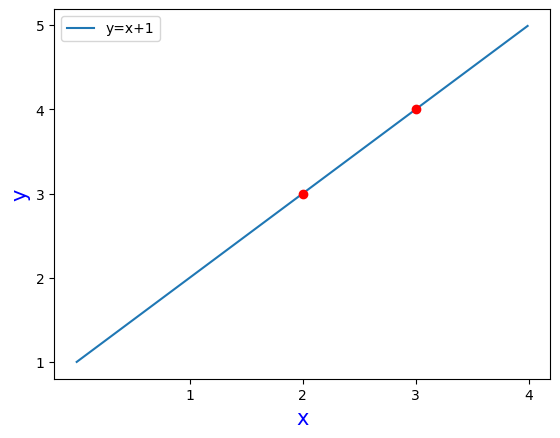
해당 그림을 보면 주어진 데이터들이 $y=x+1$이라는 식에 정확히 핏 하는 것을 알 수 있습니다. 하지만 만약 주어진 데이터들에 정확히 핏하는 선형 모델이 없으면 어떡할까요... 확실한건 중학교까지의 지식으로는 구하기 힘들 것 같네요. 그렇다면 지금부터 알아보도록 하겠습니다!

손실함수(Cost Function)

위와같은 상황에서는 주어진 데이터 $(2, 3), (3, 4)$가 $y=x+1$에 정확히 핏하지만 대개의 경우는 이러한 선형모델을 찾기 힘듭니다. 즉, 데이터 $(x_{1}, y_{1}), (x_{2}, y_{2}), \cdots, (x_{n}, y_{n})$이 주어졌을 때 실제값 $y_{n}$과 선형모델의 예측값 $\hat{y}_{i}=wx_{i}+b$의 값에 차이가 존재한다는 것 입니다. 일단은 적절한 $w, b$를 구하기 위해 두 값의 차이를 수학적인 식으로 나타내보도록 하겠습니다. 여러방법이 있겠다만 저는 다음과 같이 나타내도록 하겠습니다.

• ${{1}\over{n}}\sum_{i=1}^{n}{(y_{i}-\hat{y}_{i})^{2}}$

이렇듯 예측값과 실제값의 차이를 나타내는 함수들을 손실함수(오차함수)라 합니다. 제가 사용한 손실함수는 평균제곱오차(MSE, Mean Squared Error)라 합니다(물론 다양한 형태가 있습니다!). 이제 저희는 실제값, 예측값의 차이를 수학적인 식으로 나타내었고 이를 토대로 적절한 $w, b$를 찾아가도록 하겠습니다!

행렬을 이용한 풀이

우리는 위 손실함수를 이용한 수학적인 풀이를 통해 $w, b$를 구할 수 있습니다. $(x_{1}, y_{1}), (x_{2},y_{2})$ 두개의 데이터가 주어졌을 때 션형 모델의 예측값을 다음과 같이 행렬로 나타낼 수 있습니다.

• $\hat{y}_{1} = wx_{1} + b$
• $\hat{y}_{2} = wx_{2} + b$
• $\begin{pmatrix}\hat{y}_{1} \\\hat{y}_{2}\end{pmatrix}$ = $\begin{pmatrix}x_{1}&1 \\x_{2}&1\end{pmatrix} \begin{pmatrix}w \\b\end{pmatrix} ,\mathbf{\hat{Y}} = \mathbf{X}\mathbf{w}$

또한 각 데이터에 관한 손실(에러)는 다음과 같이 나타낼 수 있습니다.

• $\begin{pmatrix}e_{1}\\e_{2}\end{pmatrix} = \begin{pmatrix}y_{1}-\hat{y}_{1}\\y_{2}-\hat{y}_{2}\end{pmatrix} = \begin{pmatrix}y_{1}-(wx_{1}+b)\\y_{2}-(wx_{2}+b)\end{pmatrix}, \mathbf{E} = \mathbf{Y}- \mathbf{\hat{Y}}=\mathbf{Y}-\mathbf{X}\mathbf{w}$

평균제곱오차는 평균 텀(${{1}\over{n}}$)을 제외하고 다음과 같이 간단히 나타낼 수 있습니다.

• $\mathbf{E}^{T}\mathbf{E} = {e_{1}}^{2} +{e_{2}}^{2} = (y_{1}-{\hat{y}_{1}})^{2} + (y_{2}-{\hat{y}_{2}})^{2}$

이를 조금만 더 전개해보자.

• $\mathbf{E}^{T}\mathbf{E} =(\mathbf{Y}-\mathbf{X}\mathbf{w})^{T}(\mathbf{Y}-\mathbf{X}\mathbf{w})=\mathbf{Y}^{T}\mathbf{Y}-2\mathbf{Y}^{T}\mathbf{X}\mathbf{w}+\mathbf{w}^{T}\mathbf{X}^{T}\mathbf{X}\mathbf{w}$

식은 좀 복잡해 보이지만(결과 값이 스칼라 일때 $\mathbf{A}^{T}\mathbf{B}=\mathbf{B}^{T}\mathbf{A}$인 것을 기억해서 전개하면 된다!) 해당 식의 최소값을 찾는 것이 우리는 손실의 최소값을 찾는 것이므로 주어진 데이터에 가장 최적화된 $w, b$를 찾았다고 할 수 있을 것이다.

찾는 방법은 아주 간단하다! 잘 생각해보면 해당 표현된 손실함수 자체가 볼록한(convex)한 2차함수들이 합이므로 결국 볼록하다. 따라서 해당 식을 우리가 찾는 변수들에 대해 미분하고 미분값이 $0$인 부분만 찾는다면 최적화된 값들을 찾을 수 있다. $\mathbf{w}$에 대해서 미분해보도록 합시다!

• ${{\partial{\mathbf{E}^{T}\mathbf{E}}}\over{\partial{\mathbf{w}}}} = -2\mathbf{Y}^{T}\mathbf{X}+2\mathbf{w}^{T}\mathbf{X}^T\mathbf{X}=0$

즉 아래와 같이 $\mathbf{w}$를 구할 수 있습니다!

• $\mathbf{w}=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{Y}$

매우 간단한 식으로 선형 모델을 구할 수 있습니다. 다만 행렬연산의 시간복잡도는 작지 않으며 해당 식에서는 $\mathbf{w}$의 원소가 $w, b$로 고정되어있을 때 $\mathbf{X}$, $\mathbf{Y}$가 모든 데이터에 대한 정보를 포함하고 있음으로 데이터의 갯수가 $n$일때 $O(n^4)$이 됩니다. 그렇다면 다른 방법도 알아보도록 합시다!

경사하강법 (Gradient Descent)

아이디어는 매우 간단합니다. 위 행렬을 이용한 풀이에서도 알 수 있듯이 손실함수를 최소화 하는 것으로 가장 적절한 선형모델을 찾을 수 있습니다. 이렇듯 경사하강법은 매순간 손실함수를 감소시키는 방향으로 파라미터(변수)들을 업데이트하며 이 과정을 반복하여 적절한 파라미터들을 찾는 것입니다. 즉, 경사하강법을 한마디로 하면 다음과 같습니다.

경사하강법은 현재의 손실함수를 감소시키는 방향으로 파라미터들을 업데이트 하는 것이다.

손실함수를 감소시키기 위한 가장 쉬운 방법을 미분을 통한 직선의 기울기를 활용하는 것 입니다. 함수의 특정 지역에서의 미분값은 함수값이 가장 급변하는 방향의 기울기를 나타냅니다. 즉, 손실함수가 가장 빠르게 감소할 수 있는 방향을 알 수 있습니다.

현재 손실값이 $E$이고 이를 감소 시키기 위해 $w$ 값을 조정해본다고 가정하겠습니다. 그렇다면 손실값을 줄이기 위해 $w$ = 현재 $w$ 값 - (현재 $w$ 값에서 손실함수의 기울기)와 같은 식을 세울 수 있습니다. 해당식은 기울기가 양수라면 $w$의 값을 감소시켜야하고 음수라면 증가시켜야하기 때문에 -부호가 들어갔습니다. 결론적으로 이를 식으로 나타내면 아래 그림과 같이 $w = w-\alpha{{\partial{E}}\over{\partial{w}}}$과 같은 식으로 나타낼 수 있습니다. 여기서 $\alpha$는 학습률(learning rate)를 의미하며 $w$가 조정되는 정도를 조절하는 역할을 가지고 있습니다.

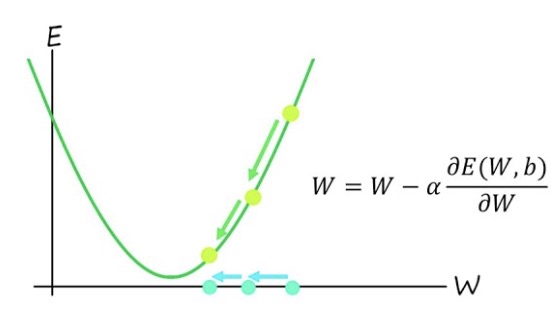
저희는 위와 같이 행렬로 인한 풀이가 없어도 이러한 경사하강법을 반복적으로 적용하여 손실값이 매우 적은 선형 모델을 찾을 수 있습니다!

코드를 통한 실험

저는 경사하강법을 통해 데이터에 적합한 선형모델을 찾을 수 있는지 코드를 통한 실험을 해보았습니다! 코드는 다음과 같습니다(제 깃허브에서도 찾아볼 수 있습니다).

import matplotlib.pyplot as plt
import numpy as np

#랜덤으로 데이터 생성
x = 5*np.random.random_sample(3)
y = 3*np.random.random_sample(3)

#랜덤으로 초기 w, b 값 설정
w = np.random.random_sample(1)
b = np.random.random_sample(1)

#에폭과 러닝 레이트를 설정
#에폭은 경사하강법 반복 횟수를 의미
epoch = 3000
learning_rate = 0.05

for _ in range(0, epoch+1):
  #현재의 선형 모델로 계산된 예측값
  predicted_y = w*x+b

  #손실 함수 값 
  cost = np.mean((y-predicted_y)**2)
  #print(f'현재 손실 값: {cost}')

  w = w - learning_rate*np.mean((-2*x*(y- predicted_y)))
  b = b - learning_rate*np.mean((-2*(y- predicted_y)))
  if _%10 == 0:
    print(f'{_} 반복 손실 값: {cost}')
    plt.scatter(x, y, color='red')
    plt.xlim(0, 5)
    sample = np.arange(0, 5, 0.01)
    plt.plot(sample, sample*w+b)
    plt.show()

해당 코드로 실험하였을 때 다음 사진이 처음에 랜덤으로 선택된 선형모델입니다.

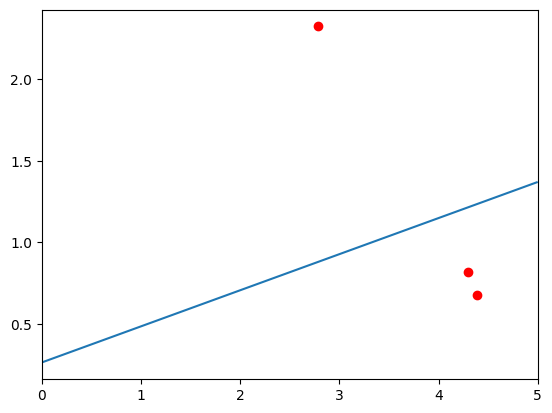
다음 사진은 경사하강법을 통해 모델링한 선형 모델입니다.

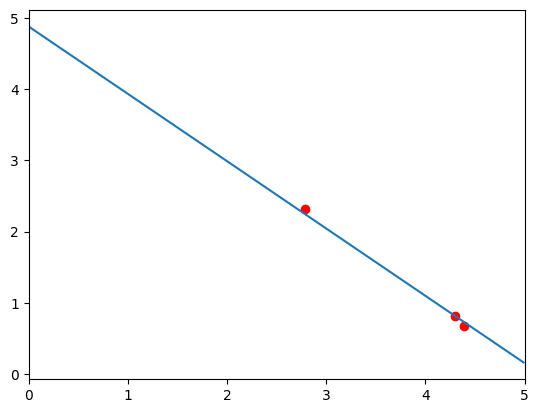
결과를 보시면 적절한 선형모델을 아주 잘 찾은 것을 알 수 있습니다 :) 이번 포스팅에서는 선형회귀가 무엇인지, 선형회귀를 풀기위한 몇가지 방법등을 포스팅하였습니다! 저는 딥러닝에 관련된 내용을 포스팅할 계획이라 다소 방법론적인 접근에만 집중하였던 것 같습니다. 다음 포스팅에서는 간단한 Perceptron에 대해 다뤄볼 수 있도록 하겠습니다!