기술 통계(descriptive statistics): 자료를 요약(summarize)하고, 정리(organize)하여 이해하기 쉽게 제시함.
1. 중심경향값(central tendency)
1) 평균(mean): 자료의 모든 숫자를 더한 뒤 값의 개수로 나눈 값
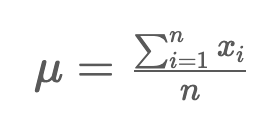
- 분포에 있는 모든 값에 민감함.
- 분포에 있는 극단값에 영향을 많이 받음.
<예시>
1, 2, 7, 100
평균: (1+2+7+100)/4 = 27.52) 중앙값 (median): 값을 크기 순서대로 나열했을 때 가장 중앙에 있는 값
- 자료의 개수가 짝수일 경우, 가장 중앙에 있는 값
자료의 개수가 홀수일 경우, 중앙에 있는 두 값의 평균 - 평균과 달리 분포에 있는 극단값에 영향을 받지 않음.
<예시>
1, 2, 7, 100
중앙값: (2+7)/2 = 4.53) 최빈값(mode): 가장 빈번하게 발생하는 값
- 연속 변수보다는 범주형 변수에서 유용함.
<예시>
1, 1, 3, 7
최빈값: 1 데이터 분석 적용점 : 데이터 분석에서 일반적으로 평균을 많이 활용함. 평균은 데이터에 있는 모든 값에 민감하고, 특히 극단값에 영향을 많이 받는다는 특징이 있음. 따라서 데이터가 정규분포가 아니거나 극단값이 있는 상황에서는 평균보다 중앙값을 사용하는 것이 자료를 더 잘 대표할 수 있음.
2. 변산도(variability)
1)범위(range): 분포에서 가장 큰 값에서 가장 작은 값을 뺀 값.
- 양 극단에 있는 값에 의해 구하기 때문에 다른 값들을 반영하지 않음.극단 값의 영향을 많이 받음.
데이터 분석 적용점: 데이터에 오류가 있는지 확인할 때 유용함. 척도가 있는 데이터라면 척도 범위를 벗어난 범위의 값이 존재한다면 데이터에 오류가 있을 가능성이 있음.
2)사분위수 범위(interquartile range): 75%와 25%에 위치한 값의 차이
IQR = Q3 - Q1
(Q1 = 25% , Q2 = 50%, Q3 = 75%)
Q2는 중앙값과 동일함.- 극단값의 영향이 적음.
<예시>
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Q1 --> 3
Q2 --> 5.5
Q3 --> 8
IQR = Q3 - Q1 = 5- 집단의 분포가 매우 흩어졌거나 양 극단에 있는 값이 변산도에 크게 영향을 준다고 판단할 때 사용하면 좋음.
3)분산(variance): 편차제곱의 평균, 값들이 평균에서 떨어진 거리를 제곱한 값의 평균
- 편차(deviation): 특정 값이 평균으로부터 떨어진 거리
*편차의 합은 0이 되기 때문에 분산 혹은 표준편차를 이용함.
[모집단의 분산]
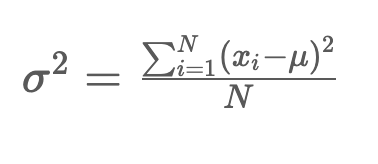
[표본집단의 분산]
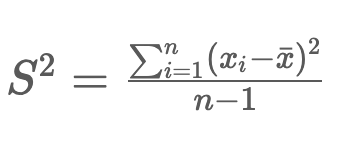
4)표준편차(standard deviation): 분산의 제곱근
- 가장 신뢰로운 변산도를 원할 때 사용함. 편차를 제곱하면 크기가 커지므로 표준편차를 많이 사용함.
[모집단의 표준편차]
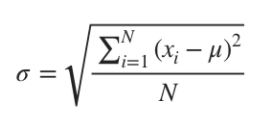
[표본집단의 표준편차]
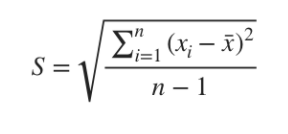
데이터 분석 적용점: 중심경향값과 변산도를 함께 고려해야함. 그렇지 않으면 분포에 대해 단편적인 정보만 얻게 됨. 보통 평균과 표준편차를 함께 제시함.

.jpg)