[통계 이론] 모집단과 표본

1. 모집단과 표본

모집단(population)	표본(samples)
연구의 관심이 되는 집단 전체	관찰을 위해 추출된 모집단의 부분 집단

➡️ 대부분의 경우 집단 전체에 대한 전수조사가 가능하지 않으므로 표본을 통해 모집단에 대해 추론함.

2. 모수와 통계량

모수(population parameter)	통계량(sample statistic)
모집단의 특성을 나타내는 값	표본의 특성을 나타내는 값
모평균( $μ$ )	표본평균 ( $\overline{x}$ )
모분산( $σ^2$ )	표본분산 ( $s_{x}^2$ )
모표준편차( $σ$ )	표본표준편차 ( $s_{x}$ )

⚠️ 주의: 표본의 모수, 모집단의 통계량으로 표현하지 않도록 하기.

모표준편차

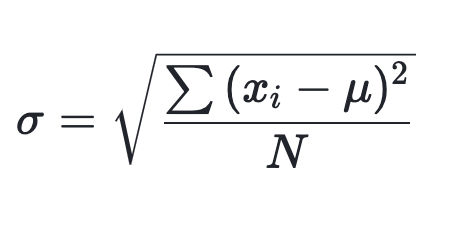
<예제>
4명의 학생들의 수학 성적은 70, 50, 80, 90이다. 다음 성적의 표준편차를 구하라.

(풀이)
𝜇 = $\frac{(70 + 50 + 80 + 90)}{4}$ = 70
$SS$ = $(70-70)^2$ + $(50-70)^2$ + $(80-70)^2$ + $(90-70)^2$ = 1000
$σ^2$ = $\frac{SS}{N}$ = $\frac{1000}{4}$ = 250
𝜎 = 15.81

정답: 15.81

표본표준편차

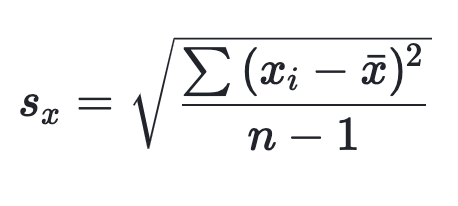
<예제>
학생들이 몇개의 과목을 수강하는지 조사하기 위해 4명을 표본으로 뽑았다. 과목 개수는 4, 6, 7, 3개이다. 다음 과목 개수의 표준편차를 구하라.

(풀이)
$\overline{x}$ = $\frac{(4 + 6 + 7 + 3)}{4}$ = 5
$SS$ = $(4-5)^2$ + $(6-5)^2$ + $(7-5)^2$ + $(3-5)^2$ = 10
$s_{x}^2$ = $\frac{SS}{n-1}$ = $\frac{10}{(4-1)}$ = $\frac{10}{3}$ = 3.33
$s_{x}$ = 1.83

정답: 1.83

• 참고: 모집단과 표본의 평균, 분산, 표준편차를 구할 수 있는 사이트
  https://www.calculatorsoup.com/calculators/statistics/variance-calculator.php