[통계 이론] 표집분포와 중심극한정리

1. 표집 방법

• 표집: 모집단에서 표본을 추출

1) 확률(무작위) 표집(random sampling)

모집단에서 각 사례가 동일한 확률로 추출됨.

(1) 단순 무작위 표집(simple random sampling)

모집단의 모든 사례를 같은 확률로 추출함.
예)모집단 사례 모두에게 번호를 부여하고 표본의 수만큼 번호를 무작위로 뽑아서 표본을 추출함.

(2) 체계적 표집(systematic sampling)

첫번재 사례를 무작위로 추출한 뒤, 매번 k번째 사례를 추출함. 주기성이 없을 때 사용해야함.
예)출구조사(투표소에서 나오는 사람들 k번째마다 조사)

(3) 층화 표집(stratified sampling)

모집단을 구성하는 계층별로 무작위로 표집함. 모집단이 서로 다른 집단으로 구성될 때 활용함. 계층은 지역, 연령, 성별 등으로 연구 목적에 따라 달라짐.
예)

• 비율 층화 표집: 모집단에 대한 각 계층의 비율대로 각 계층에서 사례를 추출.
  예) 모집단 1000명에서 표본 100명을 추출할 때 남자와 여자 비율이 6:4이면 남자 600명 중 60명을, 여자 400명 중 40명을 추출함.
• 비비율 층화 표집: 모집단에서 각 계층마다 추출할 때 모집단에 대한 계층의 비율이 아닌 다른 비율로 사례를 추출.
  예) 모집단 10000명에서 표본 100명을 추출할 때 남자와 여자 비율이 1:9이면 남자 100명 중 20명, 여자 900면 중 80명을 추출함.

(4) 집락 표집(clustered sampling)

자연스럽게 형성된 집락에 따라서 무작위로 표집함.
예) 서울시 상인 대상 설문 조사시 특정 구를 5개를 무작위로 선정해서 사례를 추출함.

2) 비확률(편파된) 표집(biased sampling)

모집단에서 어떤 사례가 다른 사례에 비해 추출될 확률이 높음.

(1) 의도적 표집 (purposive sampling)

특정 집단이 모집단을 잘 대표할 것으로 판단하여 특정 집단에서 사례를 추출함.

(2) 편의(우연적) 표집 (convenience sampling)

연구자가 쉽게 얻을 수 있는 사례를 표본으로 추출함.
예) 심리학 연구 참가자를 심리학 교양 수업을 수강하는 대학생들을 대상으로 함.

(3) 할당 표집(quota sampling)

모집단을 구성하는 계층별로 작위적으로 표집함. 층화 표집과의 차이점은 무작위로 표집하지 않는다는 점임. 층화표집과 마찬가지로 비율, 비비율로 구분됨.

(4) 눈덩이 표집(snowball sampling)

한 사례로부터 시작하여 표본을 점차적으로 늘려가는 방법. 사례로부터 얻는 다른 사례에 대한 정보를 바탕으로 표본을 늘려감. 모집단에 대한 접근이 어려울 때 활용함.

2. 표집분포(sampling distribution of the means)

동일한 모집단에서 크기가 n인 표본을 무한히 반복 추출한 뒤, 그 평균을 가지고 만든 이론적 분포.

표집분포 시뮬레이션

• n=5인 표본을 1회 추출
  
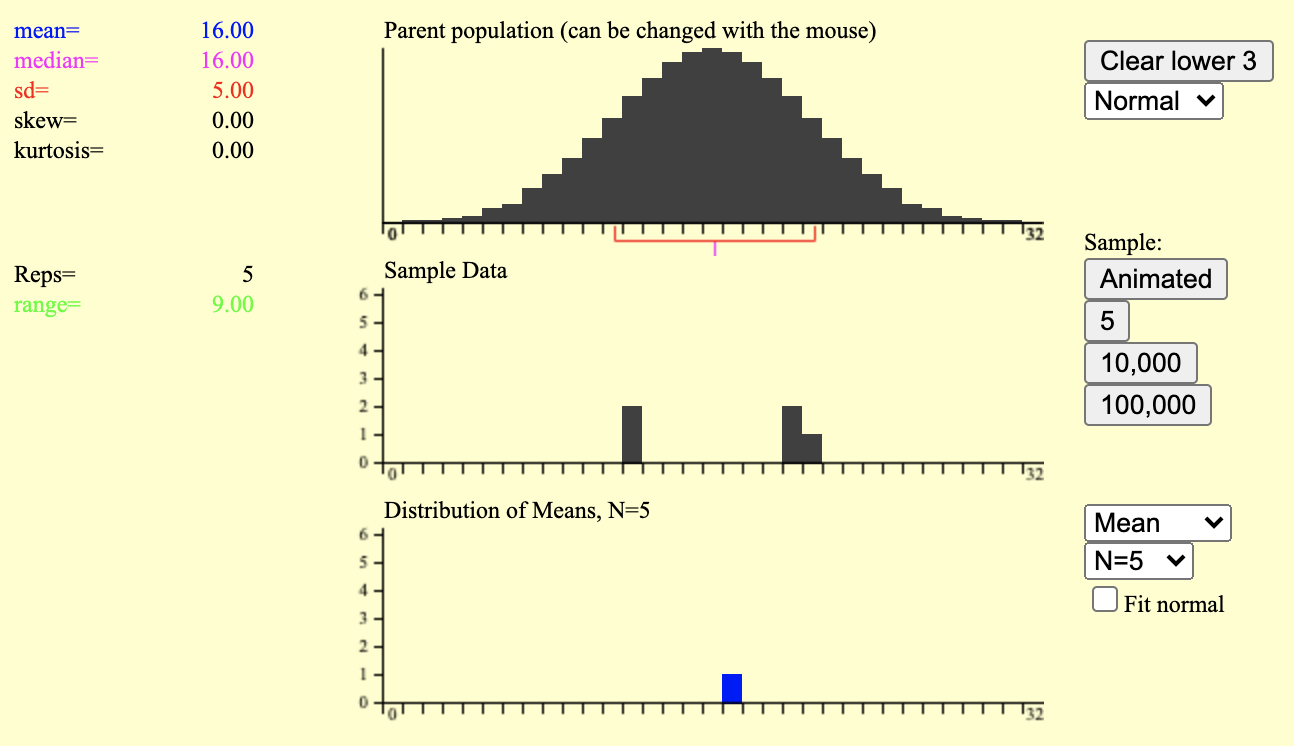
• n=5인 표본을 10회 추출
  
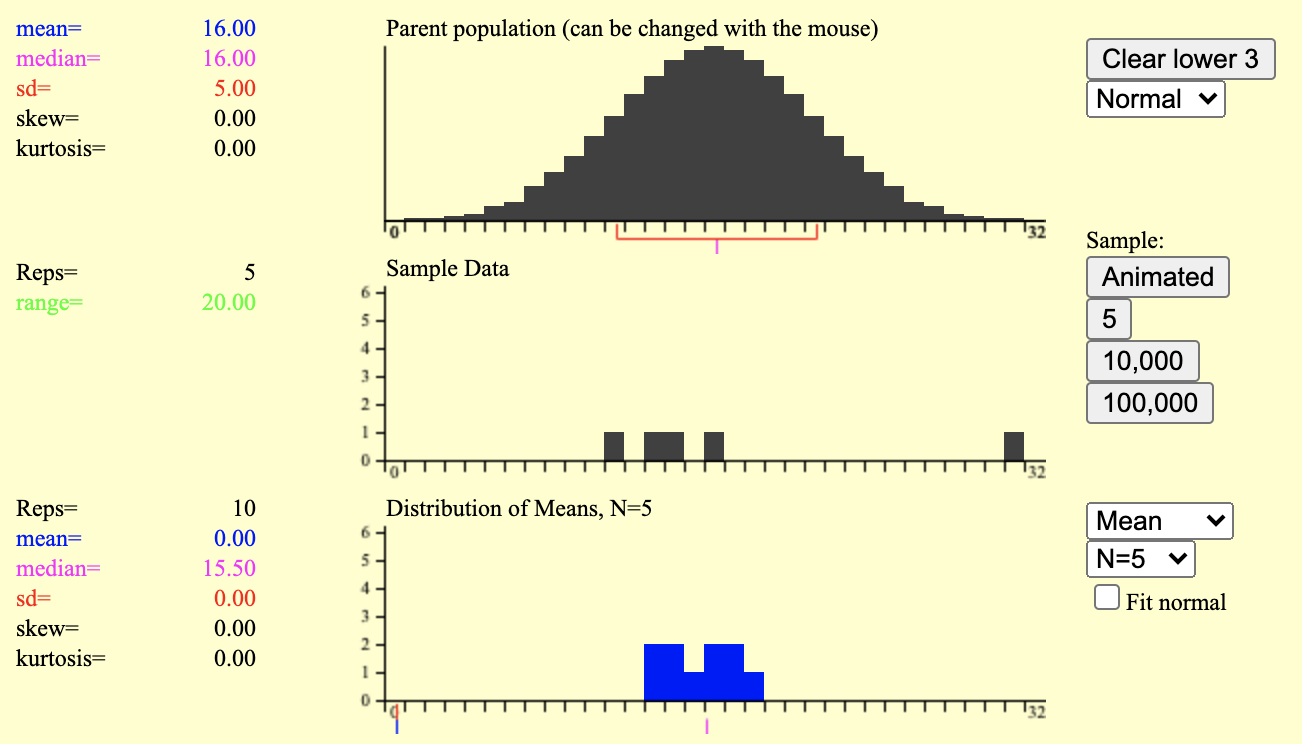
• n=5인 표본을 10,000회 추출
  
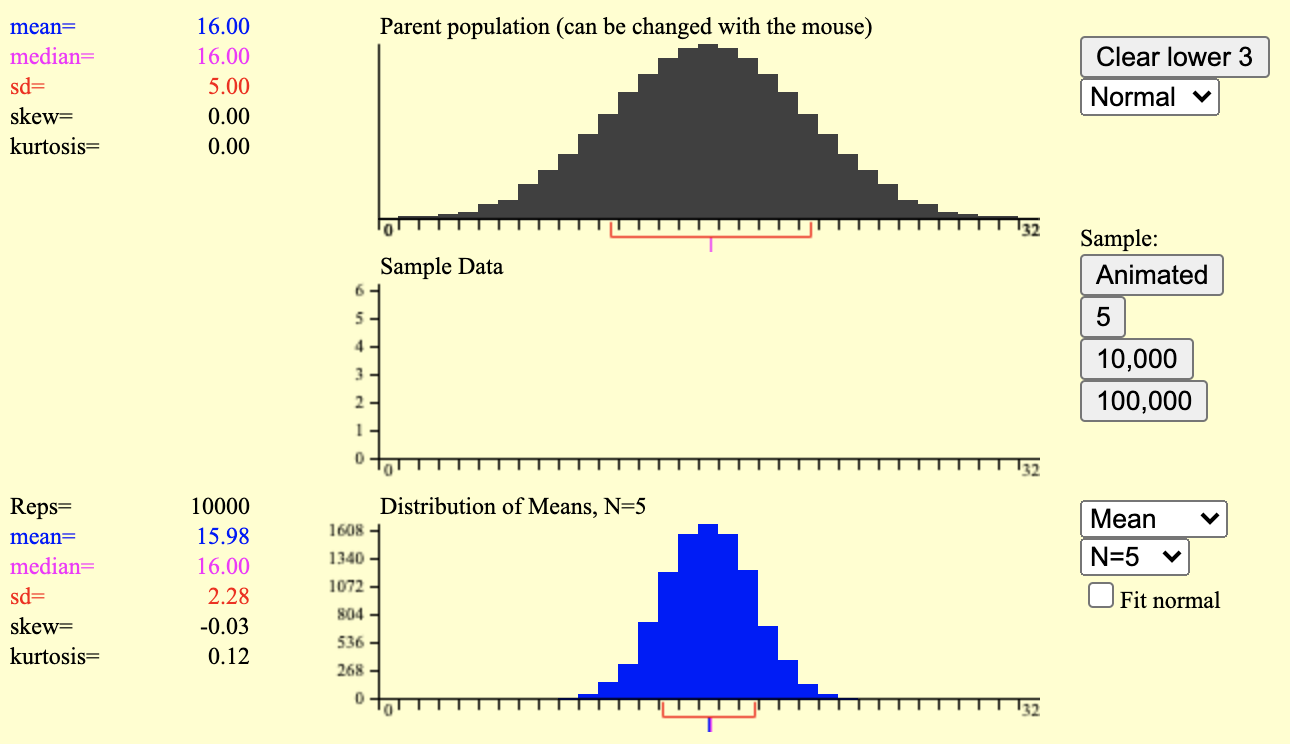
• n=5인 표본을 100,000회 추출
  

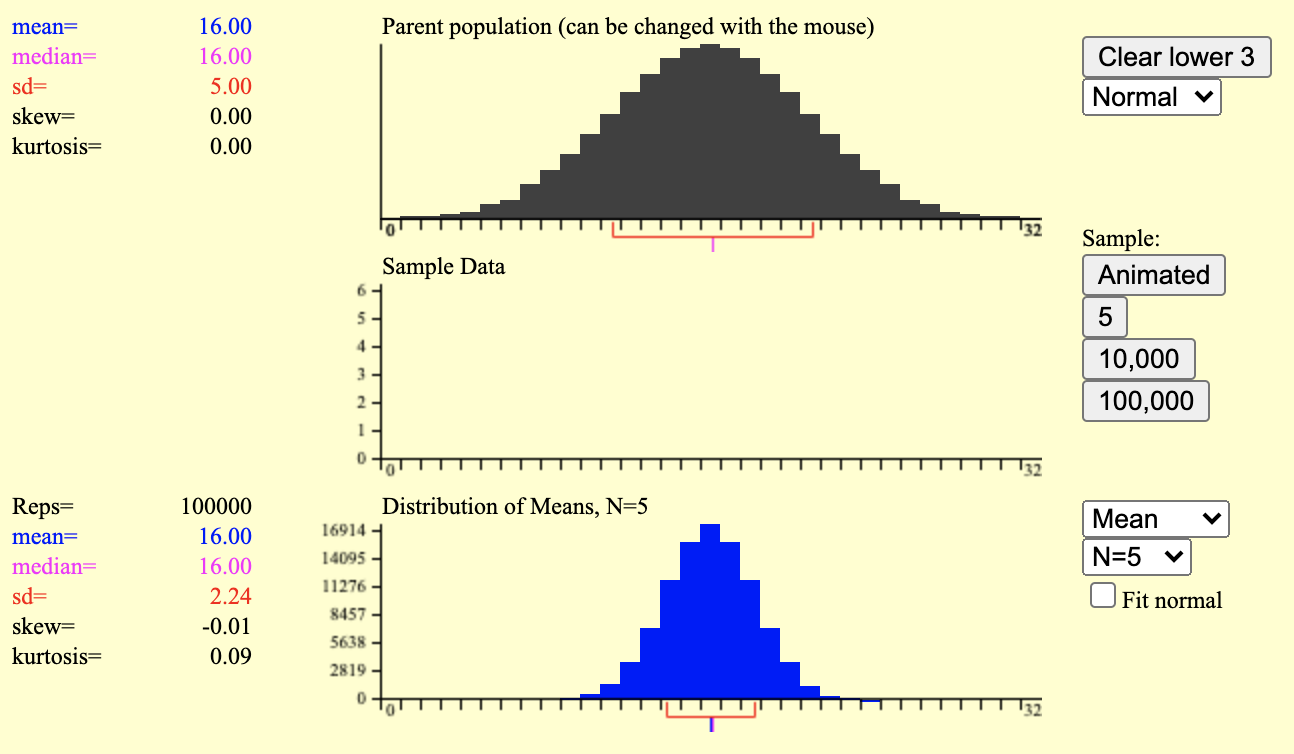
출처: https://onlinestatbook.com/stat_sim/sampling_dist/index.html

표준오차(SE: standard error)

: 표집분포의 표준편차

중심 극한 정리

1) 표본의 크기가 충분히 크면(n > 30 이면) 표집분포는 근사적으로 정규 분포이다.
2) 모집단의 분포가 정규분포이면 표본의 크기와 상관 없이 표집분포는 정규분포이다.
3) 표집분포의 평균은 $μ$ 이다.
4) 표집분포의 표준편차(표준오차)는 $\frac{σ}{\sqrt N}$ 이다.

• 표준오차의 특징
  • 표준오차는 표본의 크기가 커지면 작아진다.
    ⬅️ 표본의 크기가 커지면 각 표본의 평균 사이 거리가 가까워지기 때문이다.
  • 표준오차는 모표준편차에 비해 작다.

모집단 분포, 표본분포, 표집분포 평균과 표준편차

종류	평균	표준편차
모집단 분포	$μ$	$σ$
표본분포	$\overline{x}$	$s_{x}$
표집분포	$μ_{\overline{x}} = μ$	$σ_{\overline{x}} = \frac{σ}{\sqrt N}$