[프로그래머스] 가장 먼 노드 C++

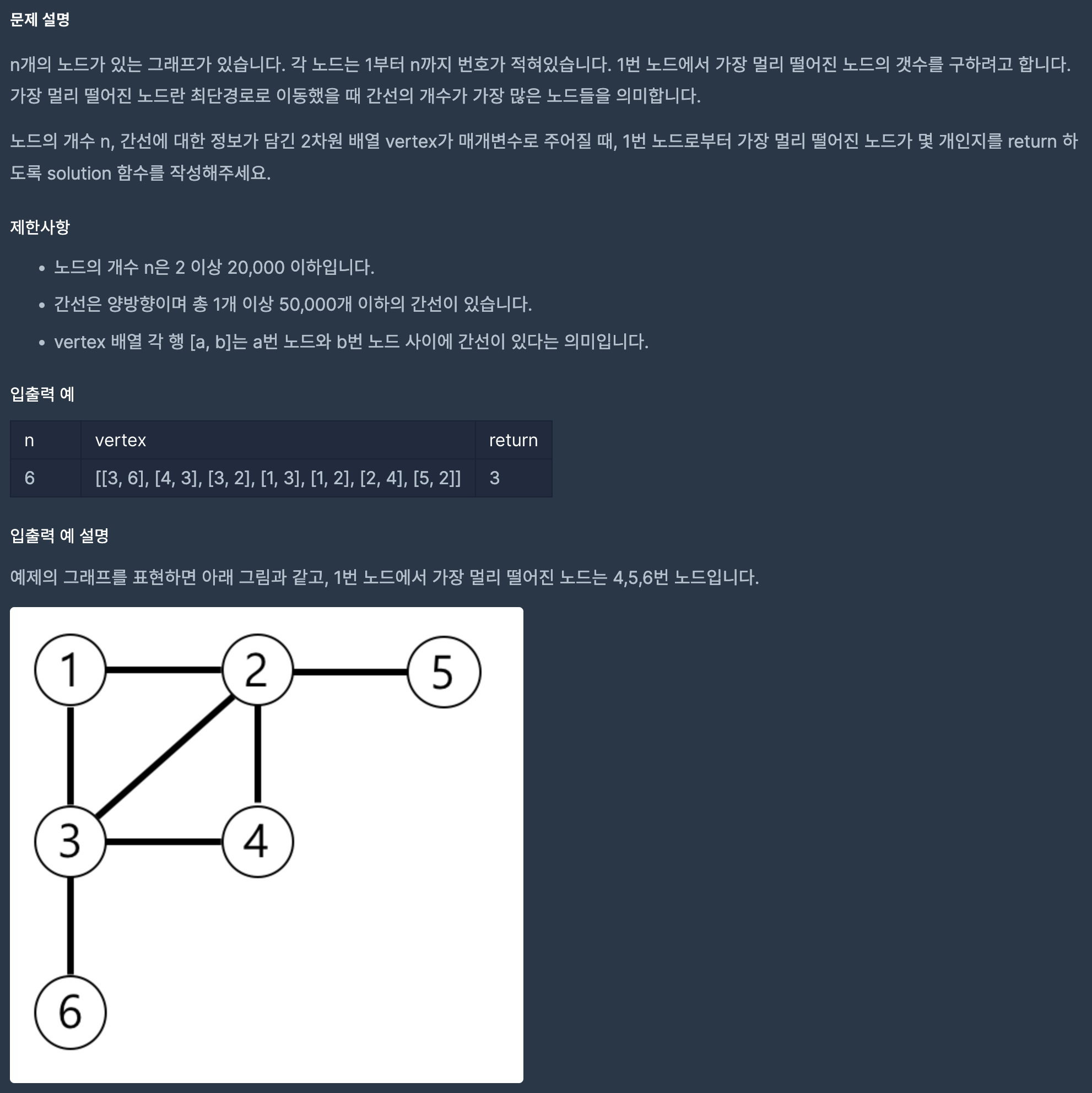
"가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다."

bfs를 안다면 단번에 해법이 떠오르는 문제다.

백준으로 알고리즘 공부를 해오던 나에게 이 문제가 level.3라는 것이 의아했다.

하지만 보통의 사람이 배경지식이 전혀 없는 상태에서 dfs나 bfs 같은 아이디어를 떠올리기란 사실 쉽지 않다. 처음으로 완전탐색 문제를 마주했을 때 좌절했던 나의 모습을 상기할 수 있었다...

---

이번 포스트에서 bfs를 어떻게 사용하는 지는 서술할 필요는 없을 것 같다. 이미 훌륭한 글들이 많다.

하지만 스스로 복습하는 차원에서 최단거리를 찾을 때 bfs를 이용하는 이유를 적어 보려한다.

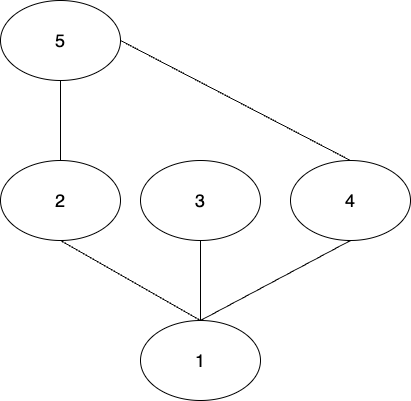
다음과 같은 그래프가 있다고 하자. 1번노드에서부터 탐색을 시작하여 '최단거리'를 구하려 한다. 이미 방문한 노드는 다시 방문하지 않는다.

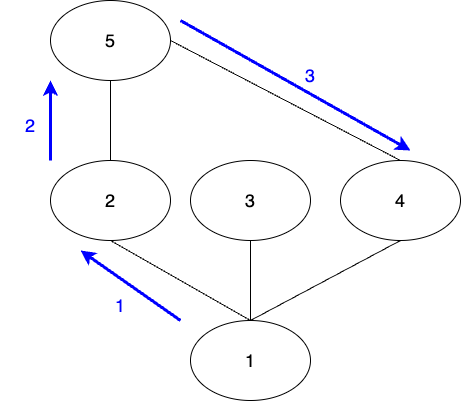
dfs로 탐색했을 때의 과정이다. 1->2 간선부터 탐색을 시작한다면 다음과 같다.

1. 1 -> 2
2. 2 -> 5
3. 5 -> 4

dfs는 깊이우선탐색이다. 말그대로 탐색을 할 때 계속해서 깊게 들어가는 것이다.

1->2->5 까지는 최단거리로 탐색을 진행했지만 1->4까지는 3번만에 탐색을 완료한다.

하지만 1->4로 한번에 갈 수 있는 간선이 존재하기 때문에 dfs로는 최단거리를 구할 수 없다.

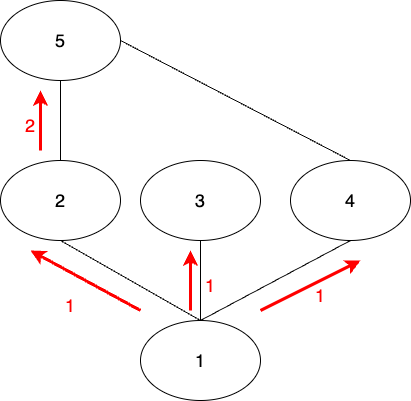
bfs에서는 방문하는 순서가 다르다.

여기선 1노드와 맞닿아있는, 그러니까 1노드와 연결되어 있는 노드부터 전부 다 방문한다.

그림을 보면 각 노드를 방문한 순서(깊이)가 최단거리인 것을 알 수 있다.

---

풀이

최단경로를 구하기 때문에 bfs를 이용한다.

'다만 가장 거리가 먼 노드들이 몇개' 인지를 구해야 하기 때문에 max_dist를 선언하고 탐색할 때마다 '최장거리'를 기록해두겠다.

그리고 탐색을 모두 마치면 모든 노드들까지의 거리를 기록해둔 dist[]를 반복문으로 돌며 dist[i] == max_dist의 갯수를 리턴한다.

#include <string>
#include <vector>
#include <queue>
#include <algorithm>

#define INF 20001

using namespace std;

vector<int> edges[20001];
int dist[20001];
int max_dist = 0;

void bfs()
{
    fill(&dist[0], &dist[20001], INF);
    queue<int> q;
    q.push(1);
    dist[1] = 0;
    
    while (!q.empty())
    {
        int here = q.front();
        q.pop();
        
        max_dist = max(max_dist, dist[here]);
        
        for (int i = 0; i < edges[here].size(); ++i)
        {
            int there = edges[here][i];
            
            if (dist[there] != INF)
                continue;
            
            dist[there] = dist[here] + 1;
            q.push(there);
        }
    }
}

int solution(int n, vector<vector<int>> edge) {
    for (int i = 0; i < edge.size(); ++i)
    {
        int a = edge[i][0];
        int b = edge[i][1];
        
        edges[a].push_back(b);
        edges[b].push_back(a);
    }
    
    bfs();
    
    int answer = 0;
    
    for (int i = 1; i <= n; ++i)
        if (dist[i] == max_dist)
            ++answer;
    
    return answer;
}