[프로그래머스] 순위 C++

'순위를 매길 수 있는 선수의 수'를 리턴하는 문제이다.

어떤 경우에 순위를 매길 수 있을까? 해당 선수의 관한 다른 모든 선수들의 승패여부를 알 수 있다면 그 선수가 몇 등인지 순위를 매길 수 있다.

문제를 단순화하기 위해 2번 선수와 다른 선수의 상관관계를 그래프로 그려보자.

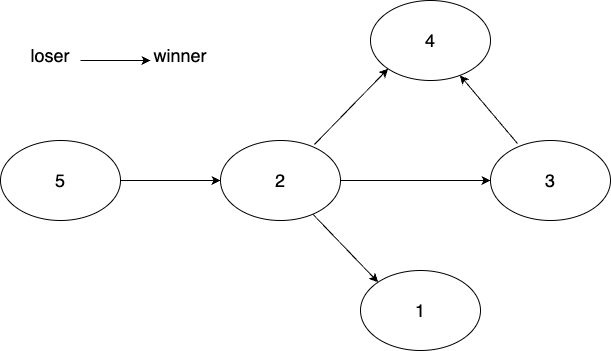
문제에서 주어진 예시를 패자에서 승자로 이어지는 단방향그래프로 그려보았다.

2번 노드에서 탐색하면 1, 3, 4번 노드를 방문하게 되며 이는 2번 선수는 1,3,4번 선수에게 패한다는 것을 나타낸다.

그럼 이 그래프 만으로 2번선수의 순위를 알 수 있을까? 아니다. 아직 5번과 2번의 관계를 알 수 없다. 정확히 말하면 우리(인간)은 그래프를 보며 5번이 2번에게 패배한다는 것을 알 수 있지만 그래프를 '탐색'하는 과정에서는 2번과 5번의 관계가 나타나지 않는다.

그러므로 우리는 역방향그래프가 하나 더 필요하다. 위 그래프는 패자->승자 그래프였지만, 승자->패자 그래프가 하나 더 필요하다.

승자->패자 그래프에서 2번노드를 기준으로 탐색하면 '2번이 누구에게 이기는 지'를 알 수 있을 것이다.

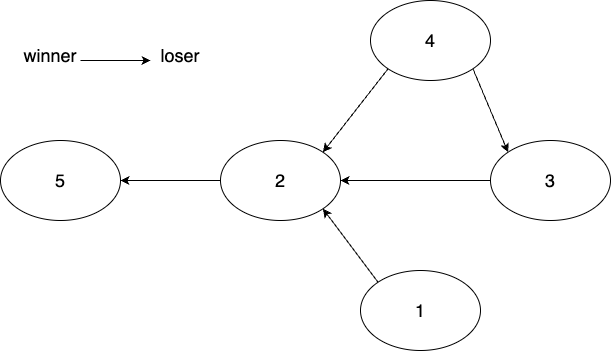
2번노드에서 탐색한다면 5번 노드를 방문할 수 있다.

그렇다면 위에서 언급한 순위를 매길 수 있는 조건을 충족한다.

두 그래프를 모두 탐색했을 때 해당 노드를 제외한 다른 모든 노드들을 방문했다면 순위를 매길 수 있는 것이다. (모순이 없는 예시만이 주어지기 때문에 두 그래프에서 중복된 노드를 탐색할 일은 없다.)

나의 경우에는 bfs를 이용해 탐색을 진행하였고 모든 노드를 두 번씩 탐색했다.

#include <string>
#include <vector>
#include <queue>
#include <string.h>

using namespace std;

vector<int> edges[2][101]; // 0 = lose_to, 1 = win_to
bool visited[2][101];

bool solve(int n, int start)
{
    int cnt = 0;
    memset(visited, false, sizeof(visited));
    
    queue<int> q;
    q.push(start);
    visited[0][start] = true;
    
    while(!q.empty())
    {
        int here = q.front();
        q.pop();
        
        for (int i = 0; i < edges[0][here].size(); ++i)
        {
            int there = edges[0][here][i];
            
            if (!visited[0][there])
            {
                ++cnt;
                q.push(there);
                visited[0][there] = true;
            }
        }
    }
    
    q.push(start);
    visited[1][start] = true;
    while(!q.empty())
    {
        int here = q.front();
        q.pop();
        
        for (int i = 0; i < edges[1][here].size(); ++i)
        {
            int there = edges[1][here][i];
            
            if (!visited[1][there])
            {
                ++cnt;
                q.push(there);
                visited[1][there] = true;
            }
        }
    }
    
    if (cnt == n - 1)
        return true;
    return false;
}

int solution(int n, vector<vector<int>> results)
{
    for (int i = 0; i < results.size(); ++i)
    {
        int winner = results[i][0];
        int loser = results[i][1];
        
        edges[1][winner].push_back(loser);
        edges[0][loser].push_back(winner);
    }
    
    int answer = 0;
    for (int i = 1; i <= n; ++i)
        if (solve(n, i))
            ++answer;
    
    return answer;
}

누가 볼 지 모르겠지만 처음으로 코드를 올리려니 부끄럽다...

---

다른 풀이

뿌듯함도 잠시 '다른 사람의 풀이'를 보고 나면 시무룩해진다.

플로이드 워셜을 응용한 듯한 멋진 풀이가 존재한다.

 for(int k = 1; k <= n; k++)
 	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= n; j++)
			if(arr[i][k] && arr[k][j])
				arr[i][j] = true;

1. i가 k에게 지고
2. k가 j에게 진다면
3. i도 j에게 진다.