[Recommendation System] Matrix Factorization

안녕하세요! 오늘은 추천시스템의 Matrix Factorization에 대해 공부한 내용을 포스팅해보겠습니다! 틀린부분 지적해주시면 매우 감사하겠습니다!

Latent Factor Model

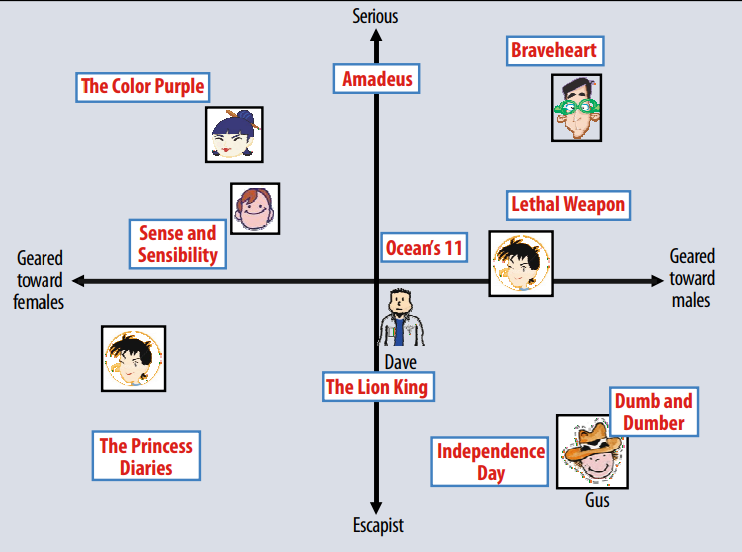
Latent Factor Model은 사용자와 아이템을 어떠한 잠재적인 특성들을 통해 나타낼 수 있다고 보는 모델입니다.

• 위 그림 처럼 실제로 아이템과 사용자가 어떠한 잠재적인 특성 (위 예시에서 남성향, 여성향 웃김, 심각함 등) 을 가지고 있다는 것입니다!

• 이러한 Latent Factor Model 에는 아래와 같은 방법들을 이용할 수 있습니다.

  • Matrix Factorization
  • Probabilistic Latent Semantic Analysis
  • Latent Dirichlet Allocation
  • Neural Networks

  방법들의 장단이 있지만 그 중 Matrix Fatorization에 집중하여 한번 알아보겠습니다.

Matrix Factorization

Matrix Fatorization의 목적은 사용자와 아이템 평점 데이터를 이용해 추상 공간을 도출하는 것입니다.

Matrix Factorization 방법은 사용자와 아이템 모두 추상 공간에서 벡터로 표현합니다.

• 사용자 벡터 : $p_u$

• 아이템 벡터 : $q_i$

이 벡터들을 이용해서

• 추상 벡터에서의 유사도를 이용해 추천 결과 생성

• 사용자에 대한 아이템의 평점 추정

  $\hat{r}_{u,i} = q_i^\top p_u$

등에 이용 가능합니다!

Matrix Factorization의 이러한 추상 벡터를 어떻게 구할까요? 그 방법은 아래 사진과 같이 사용자와 아이템의 매트릭스를 사용자의 잠재 특성 행렬과 아이템의 잠재 특성 행렬로 분해하는 것입니다.

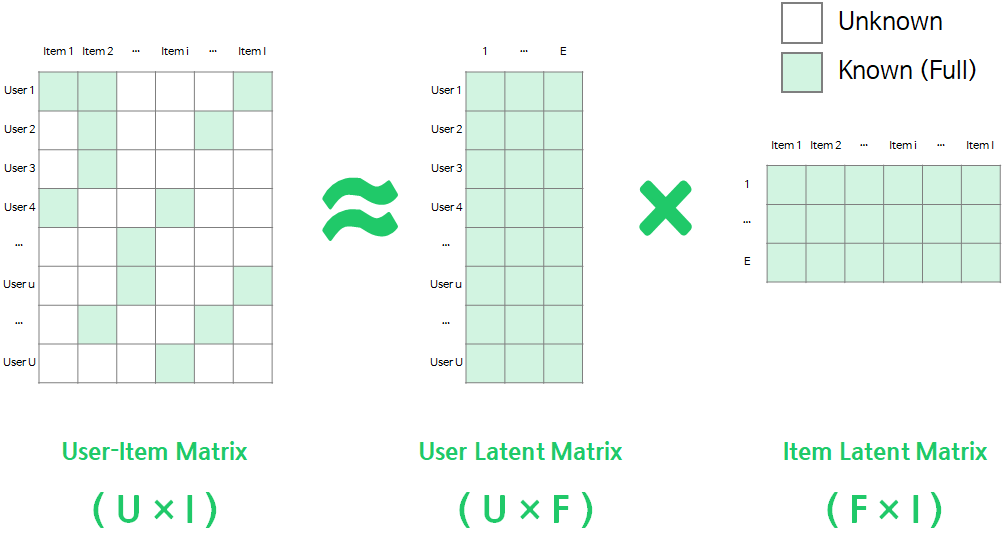
사진 출처: https://velog.io/@vvakki_/Matrix-Factorization-2

이 행렬 분해는 특이값 분해(Singular Value Decomposition)을 이용하는데요. 잠시 이 SVD에 대해 알아보고 넘어가겠습니다.

SVD

SVD는 어떠한 행렬 M이 존재할때 M이 회전과 크기 변환을 모두 포함하는 경우에 대한 해석이라고 합니다.

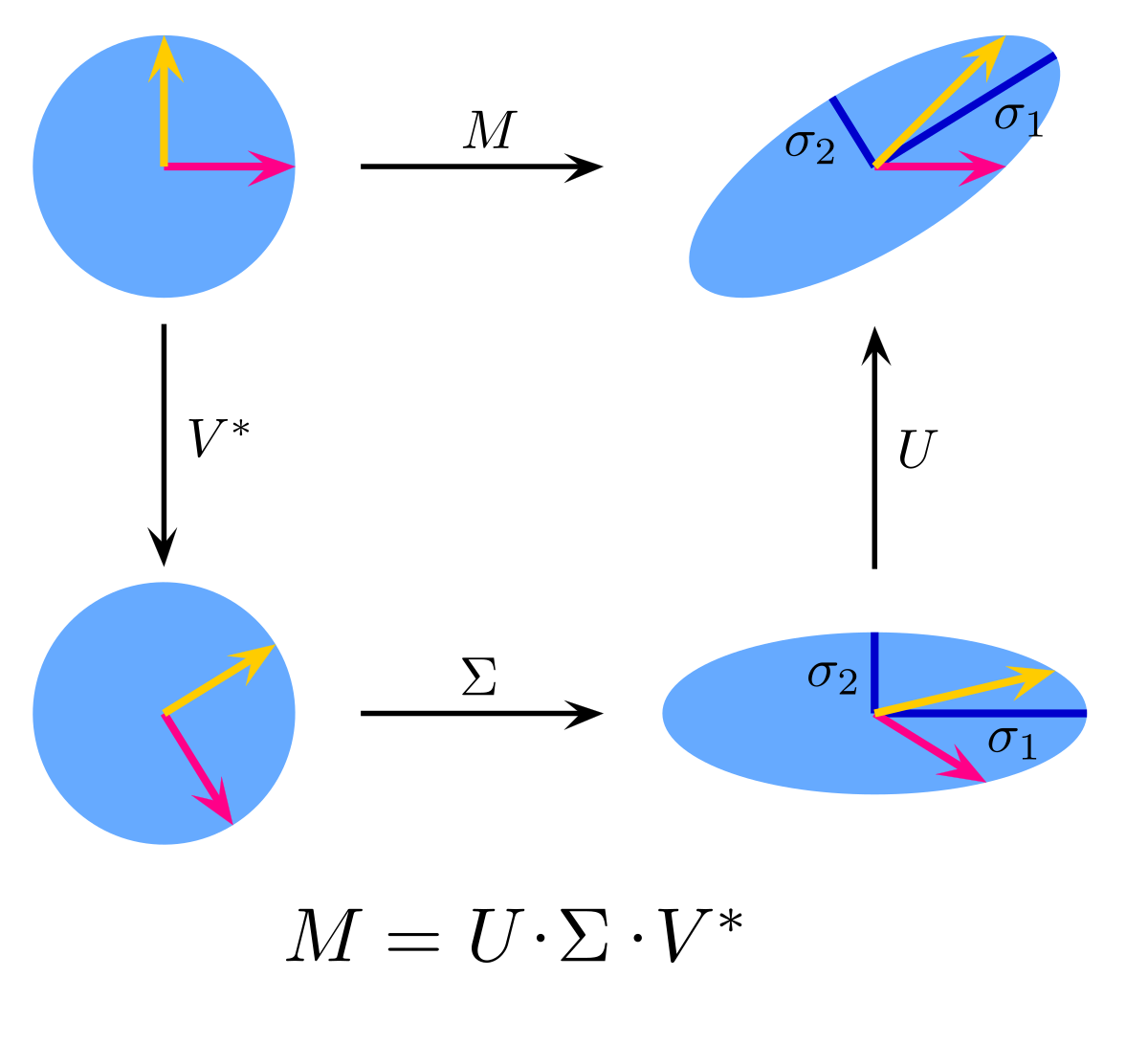
사진 출처: Wikipedia

이 사진은 SVD의 각 컴포넌트들에 대한 설명을 담고 있습니다. 사용자 입장에서는 크게 중요하지 않지만 살짝 짚고만 넘어가면 M이라는 선형변환은 $V^*$라는 회전변환 $\Sigma$라는 크기변환 그리고, $U$라는 회전변환으로 분해가 된다는 것입니다!

여기서 분해된 행렬들의 차원을 부분적으로 이용하여 차원을 축소시킬 수도 있습니다.

• 추천 시스템에 이용할때

  $M = U\Sigma V^* = U\Sigma^{1/2} \Sigma^{1/2}V^* = PQ^\top$

  로 사용자의 잠재 특성과 아이템의 잠재 특성으로 분해가 가능합니다.

• 일반적으로 위 행렬의 차원을 축소하여 이용하는데

  $M \approx U_k\Sigma_k V_k^* = U_k\Sigma_k^{1/2} \Sigma_k^{1/2}V_k^* = P_kQ_k^\top$

  로 이용합니다. 여기서 각 행렬들은 $k$ 차원의 subset 행렬을 의미합니다. 보통의 경우 버려진 성분들은 설명력이 약하기 때문에 노이즈일 가능성이 높기 때문이라고 생각되네요.

이렇게 행렬을 분해하기 위해 아래와 같은 식을 최적화합니다.

• 여기서 뒤에 $\lambda$ 항을 Regularization 항으로 데이터에 과대 적합하는 것을 막기위해 쓰이는 항입니다.

• 이 문제는 Non Convex문제 이기 때문에 해를 쉽게 구할 수 없기때문에 아래와 같은 방법을 이용합니다.

  • Stochastic Gradient Descent
  • Alternating Least Squares

  각 방법에 대한 설명은 Matrix factorization techniques for recommender systems 논문을 참고해보시기 바랍니다! 굉장히 쉬운 방법이므로 설명은 생략하겠습니다!

• 저는 이 부분에서 관측되지 않은 사용자의 평점 데이터를 어떻게 처리해야하는가가 조금 햇갈렸습니다. 관측되지 않은 element를 제외하고 위 식을 element-wise하게 loss값을 계산하여 최적화하고 이를 통해, 관측되지 않은 데이터를 추정하는 방법이라고 이해하였습니다.

  • 즉, 알 수 있는 부분만을 통하여 사용자와 아이템의 잠재 특성행렬을 얻는 것입니다.

저희는 방금 설명한 SVD 를 이용해 사용자 특성행렬 $P_k$, 아이템 특성행렬 $Q_k$로 분해가 가능함을 이용합니다. 이를 통해

를 얻어 관측되지 않은 사용자의 평점을 예측하고 추천시스템에 이용할 수 있습니다.

Bias를 고려한 성능 향상

하지만 사용자와 아이템 마다 평점 분포가 다를 것이기 때문에 $r_{u,i}$를 단순히 $q_i^\top p_u$로 예측하는 것은 이러한 분포의 차이를 고려하지 못합니다.

그렇기 때문에 아이템, 아래와 같이 사용자의 분포적인 특성을 반영하는 bias를 추가해 성능향상을 도모할 수 있습니다.

• 이때, $\mu$: 전체 평점 평균, $b_i$: 아이템 $i$의 평점 편차, $c_u$: 사용자 $u$의 평점 편차 입니다.

• 여기서 bias값들은 $q_i$와 $p_u$ 함께 최적화 하여 얻을 수 있습니다.