Matrix Factorization (2)

빠키·2020년 8월 19일

Collaborative Filtering Matrix Factorization Recommendation System 추천시스템

Recommendation System

목록 보기

3/5

Introduction

Collaborative Filtering 방법론 중 가장 대표적인 방법론인 Matrix Factorization에 대해 살펴보도록 하겠습니다. Netflix 추천 성능을 크게 상향시킨 Koren, Y., Bell, R., & Volinsky, C. (2009). Matrix factorization techniques for recommender systems. Computer, 42(8), 30-37. 논문을 참조했습니다.

Matrix Factorization

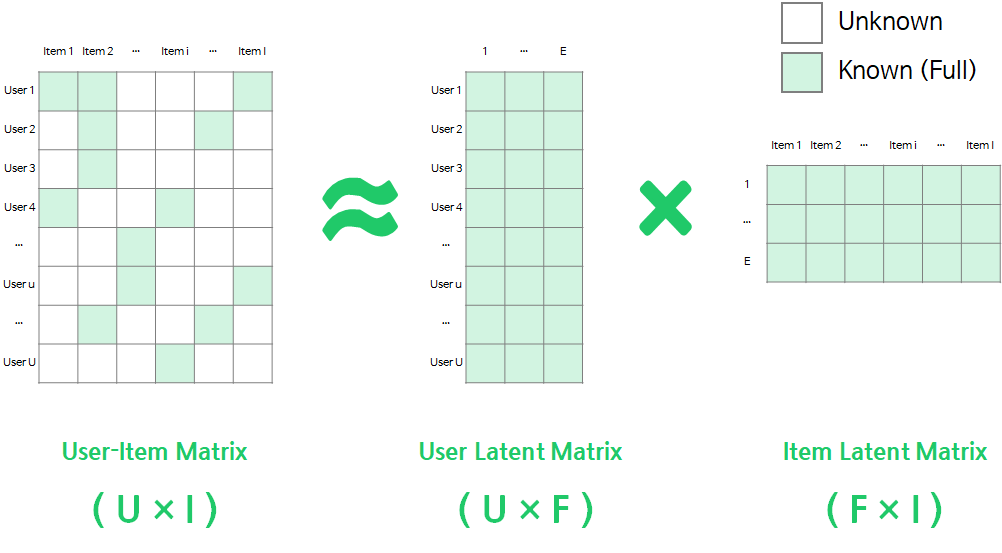Matrix Factorization은 User-Item Matrix를 F차원의 User와 Item의 latent factor 행렬곱으로 분해하는 방법을 말합니다.
User-Item Matrix의 유저 u의 아이템 i에 대한 선호도는 다음과 같이 User/Item Latent Matrix의 벡터의 곱으로 표현될 수 있습니다.

\Large\begin{aligned} \hat{r_{ui}} = q_{i}^{\intercal}p_{u} \end{aligned}

$p_{u}, q_{i} \in \mathbb{R}^f$ : User, Item Latent Matrix의 벡터
$\hat{r_{ui}}$ : 유저 u의 아이템 i 선호도 추정값

User-Item Matrix를 User/Item Latent Matrix로 맵핑(mapping)이 되면, 유저가 평가하지 않은 선호도에 대해서도 위의 수식을 통해 쉽게 추정할 수 있습니다.

비슷한 방법으로 특이값분해(Singular Value Decomposition, SVD) 방법도 있지만, User-Item Matrix와 같이 결측값이 많은 Sparse Matrix(희소행렬)에서는 적용하기가 어렵습니다.

특이값분해(Singular Value Decomposition, SVD)
특이값 분해는 (m×n)차원의 A행렬을 다음과 같이 분해하는 방법론입니다.
$\Large\begin{aligned} A = U\Sigma V^\intercal \end{aligned}$

$U$ : (m×m)차원의 직교행렬

$V$ : (n×n)차원의 직교행렬

$\Sigma$ : (m×n) 직사각 대각행렬 (대각성분 이외의 모든 값은 0)

기존의 많은 연구들이 결측치에 대한 Imputation에 집중했지만, 연산량이 많으며 부정확 Impuatation은 데이터를 왜곡시키는 단점이 있습니다.

하지만, Matrix Factorization은 Latent vector를 학습할 때, 관측된 선호도만 모델링에 활용하며, 과적합을 피하기위해 Regularized Squared Error를 사용합니다.

\Large\begin{aligned} \min_{q^*, p^*}\sum_{(u,i)\in K}(r_{ui} - q_{i}^{\intercal}p_{u})^2 + \lambda(\|q_{i}\|^2 + \|p_{u}\|^2) \end{aligned}

$K$ : 관측된 선호도 $r_{ui}$ 의 $(u, i)$

과거에 관측된 선호도에 대해서만 모델링을 하지만, 향후에 관측되지 못한 선호도를 예측하는 일반화 모델을 만드는 것이 목표이기 때문에, Regularizaion을 통해 관측 데이터에 대한 과적합을 줄이는 것입니다.

알고리즘 학습 방법

1. Stochastic Gradient Descent (SGD)

실제 선호도와 예측된 선호도의 차이를 에러로 정의
$e_{ui} = r_{ui} - q_{i}^{\intercal}p_{u}$
현재 위치의 gradient 반대방향으로 $q_{i}, p_{i}$ 를 갱신
$q_{i} ← q_{i} + \gamma \cdot (e_{ui}p_{u} - \lambda \cdot q_{i})$
$p_{u} ← p_{u} + \gamma \cdot (e_{ui}q_{i} - \lambda \cdot p_{u})$

비교적 학습시간이 짧고, 쉽게 구현할 수 있습니다.

2. Alternating Least Squares (ALS)

$q_{i}$ 와 $p_{u}$ 를 둘다 모르기 때문에 Reqularized Squared Error는 Convex 하지 않지만, 만약 둘 중 하나를 고정시키면 2차식의 최적화 문제로 해결할 수 있습니다.
ALS는 $q_{i}$ 와 $p_{u}$ 를 번갈아서 고정시키며, 최소제곱문제로 해를 구합니다.
ALS는 다음과 같은 상황에서 SGD보다 유리합니다.

병렬 시스템 : $q_{i}$ 를 학습할 때, 다른 item factor와 독립적으로 계산되기 때문에 병렬 적용이 용이함. ( $p_{u}$ 도 마찬가지)
Implicit data : Explicit data에 비해 결측치가 비교적 적기 때문에, SGD를 사용하게 되면 연산량이 증가함.

Summing up

Matrix Factorizaion : User-Item Matrix를 User/Item Latent Matrix로 행렬분해하는 방법론입니다.
유저가 평가하지 않은 결측치가 많기 때문에, SVD는 적용이 불가합니다.
SGD, ALS 알고리즘을 통해, 관측된 데이터에 대해서만 패널티를 추가하여 학습을 합니다.

Reference

빠키

하고 싶은 것이 많기에, 앞으로 할 수 있는 일들이 더 많은 Data Scientist