🚩딥러닝 기초 - part05. Linear Regression (선형 회귀 분석)

vinca·2022년 10월 25일

🌓 AI/DL - theory

목록 보기

6/24

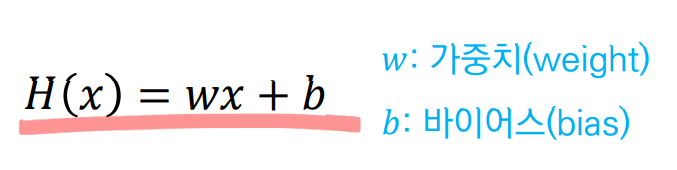
🟢 Introduction

이제 드디어 학습을 한다는 측면에서 딥러닝에 유사한 부분까지 온 것 같다!

뒤에가서 배우겠지만 퍼셉트론을 배우고, Neural Network를 배우면...진짜 딥해지는 것으로 안다.
인공지능을 맛보기로 배운지라 정확히는 모르나, CNN, RNN, GCN, GAN..생각만으로 어지러운....

🛠 회귀 분석(Regression)

Linear Regression에서 Regression부터 살펴보자! Regression은 무엇일까?

회귀 분석

자료 분석을 위한 통계학적 방법

주어진 자료의 경향성(좌표 평면에서의 data들이 나타내는 형태)를 분석하여 이러한 data들 사이의 상관관계를 추정

수학적 모델을 가정하고, 주어진 자료들을 사용하여 이 모델의 파라미터를 결정

대표적으로 선형회귀와 로지스틱 회귀가 있다.

선형회귀는 예측에 로지스틱 회귀는 분류에 사용된다. (이러한 개념은 알아두자)

이해했다면 더할 나위 없겠다만, 말이 조금 어려운가?

우리는 선형 회귀 분석부터 알아볼 것이므로, 선형회귀를 기준으로 쉽게 이해해보자.
(사실 선형회귀를 알고나면 로지스틱 회귀또한 크게 다를 빠 없다)

쉽게 말해, 사용하고자 하는 수학적 모델 ( $y=ax+b$ / 일차식이므로 선)을 가정하고, 주어진 data들로 하여금 이러한 data들을 가장 잘 나타낼 수 있는(적합한) 선을 찾는 과정. 이러한 과정을 곧 학습이라고 한다.

$a$ (기울기)와 $b$ (y절편 - bias라고 함)을 data들을 가장 잘 표현할 수 있는 선이 되도록 잘 이동하며 조정하는 것!
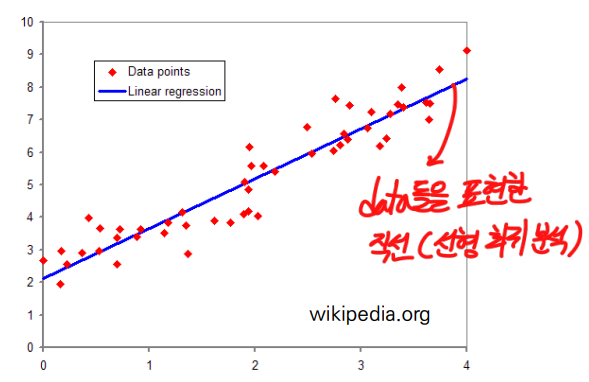
위 그림처럼 데이터들을 가장 잘 표현하는 직선(Linear)을 찾자!

🛠 Linear Regression (선형 회귀 분석)

한 개 이상의 독립 변수( $x$ )와 종속 변수( $y$ ) 사이의 선형 상관 관계를 정략적으로 추정하는 회귀 분석 방법
즉 $x$ 에 따라서 $y$ 가 결정된다.

독립 변수 : ‘x값이 변함에 따라 y값도 변한다’ 정의 하에서 독립적으로 변할 수 있는 x값

종속 변수 : 독립 변수에 따라 종속적으로 변하는 값

자 그럼 식으로 표현해보자. 사실 우리는 이미 식을 봤었다.

🛠 선형 회귀분석의 수식

다음과 같은 수식으로 표현된다!
사실상 $y=ax+b$ 에서 단순히 표현하는 변수만 조금씩 바뀌었을 뿐 동일하다.
w는 가중치(기울기)를 나타내고 b는 바이어스(y절편)을 나타낸다.
쉽게말해 그저 하나의 1차함수(직선 = Linear)일 뿐이다.

🛠 Linear Regression의 목적

일반적으로 반복적인 방법이 분석적인 방법보다 더 적합한 parameta(기울기, y절편)를 찾을 수 있다.

잘 이해가 되지 않아도 상관없다. 바로 아래 Linear Regression 예제를 통해 같은 말을 상세히 서술한다.

🛠 Linear Regression 예제

선형 회귀는 앞서 말했듯, 예측에 사용되고 이후 배우게 될 로지스틱 회귀는 분류에 사용된다.

자 그럼 선형회귀를 통해 공부시간에 대한 성적을 예측해보자.

다음과 같은 공부시간/성적에 관한 data가 있을 때, 이를 좌표평면상에 나타내면 다음과 같이 나타난다.
여기서 공부시간이 $x$ 성적은 $y$ 로 표현된다. 즉, 공부시간이 성적에 영향(변화)를 끼치므로 독립변수는 공부시간, 종속변수는 성적이 된다.

그리고나서 우리는 가설을 세우게 된다.
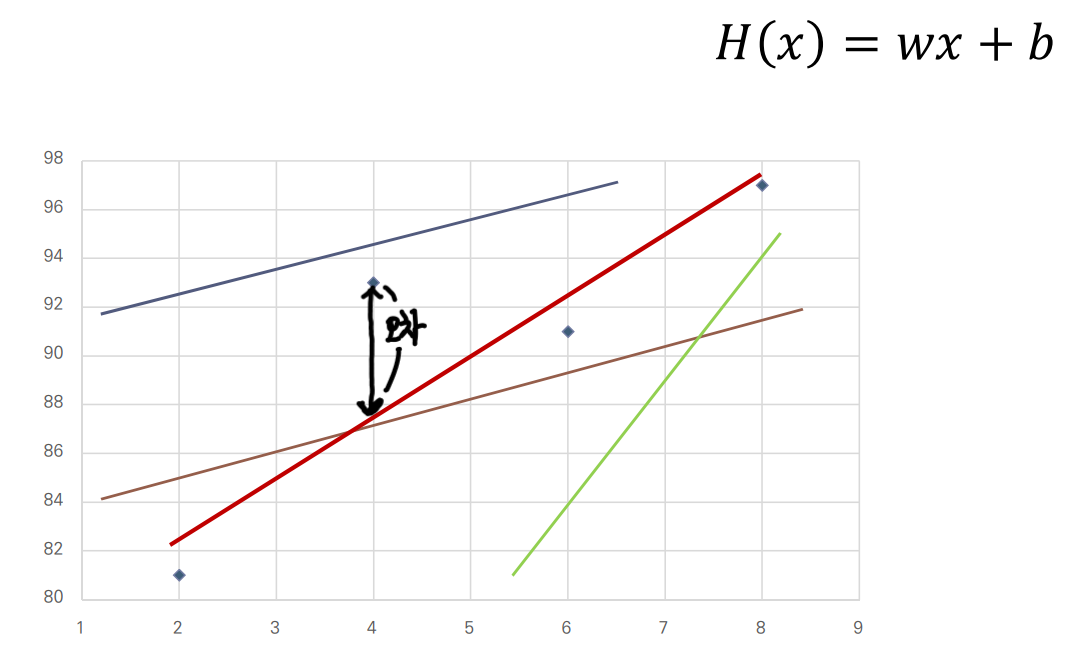
가설이라고 해야 거창할 것은 없고, 이러한 데이터를 가장 잘 표현할 수 있을것이라 예상되는 임의의 직선을 하나 긋는 것이다.

임의의 직선 $H(x)=wx+b$ 를 정의한다.

여러가지 가설 중 빨간색 선이 가장 데이터들에 가깝게 잘 표현하는 것 같다.
그럼 왜 빨간선이 가장 잘 표현하는 것 같은가?
잘 표현한다의 기준은 실제 데이터와의 오차가 된다.
오차는 가설을 세운 선과 실제 데이터간의 거리의 차다.

따라서 빨간 선이 가장 잘 표현하는 것 같다고 우리는 생각할 수 있다!

허나 저러한 선은 대략적으로 그은 것이고, 가장 잘 표현하는 빨간 선을 실제로 구하는 방법은 그럼 어떻게 될까? 바로 최소 제곱법을 이용한다.

🧩 최소 제곱법

최소제곱법이란?
근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법

Q. 제곱을하는 이유는 뭔가요?
A. 선보다 위에 있을 수도, 아래 있을 수도 있기에 각 오차에서의 부호(-/+)차이를 없애기 위해서이다.

Q. 합은 왜 합인가요?
A. 각 데이터마다 오차는 각각 발생하기 때문에 전체 데이터에서 발생한 오차를 전부 더해주는 것을 의미.

최소제곱법을 사용한 근사적인 선을 구하는 방법 2가지

잔차 제곱합(RSS: Residual Sum of Squares)을 최소화하는 가중치와 바이어스 구함

잔차 제곱합의 그레디언트(gradient) 벡터가 0이 되도록 함 (Gradient descent)

여기서는 방법 1을 사용한다. / 방법2는 Gradient descent 파트에서 기술

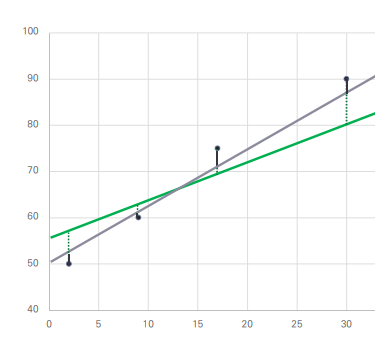
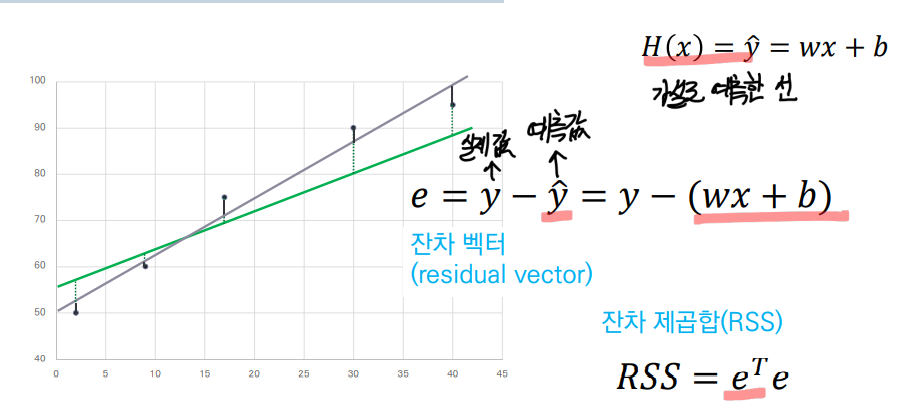
🎱 잔차란?

데이터가 가지고 있는 실제값(y)에서 예측한 $\hat y=H(x)=wx+b$ 직선을 뺀 값.
예측값은 $\hat y$ 즉, 예측한 선에 대해서 x 값을 대입해서 나온 y 결과값을 의미한다.

자, 이제 최소제곱법을 알았으니 이를 이용해서, 모델(Linear)를 계산해 보자.

🧩 최소 제곱법을 사용한 모델 추정(계산)

다음과 같은 식을 사용해서 data들을 가장 잘 표현하는 기울기 및, 절편을 추정할 수 있다.

여기서 절편(b)를 구할 때, 기울기( $w$ )가 사용되는 것을 주의하자. $w$ → $a$ 로 치환되어 표기됨

위 식을 사용해서 $x$ , $y$ 에 대한 평균/기울기/절편을 구할 수 있고, 최종적인 추정된 선을 구할 수 있다.

이를 파이썬 코드로 계산하면 다음과 같다.

#복사용 코드
import numpy as np
x = [2, 4, 6, 8]
y = [81, 93, 91, 97]
#x와 y의 평균값
mx = np.mean(x)
my = np.mean(y)
print("x와 y의 평균값:", mx, my)
#기울기 공식의 분모
divisor = sum([(mx - i)**2 for i in x])
#기울기 공식의 분자
dividend = np.sum([(mx-xi)*(my-yi) for xi, yi in zip(x, y)])
print("분모와 분자:", divisor, dividend)
#기울기와 y 절편
a = dividend / divisor
b = my - (mx*a)
print("기울기와 y 절편:", a, b)

코드 실행 결과
x와 y의 평균값: 5.0 90.5
분모와 분자: 20.0 46.0
기울기와 y 절편: 2.3 79.0
당연하지만 손으로 계산한 결과와 동일한 것을 알 수 있다.

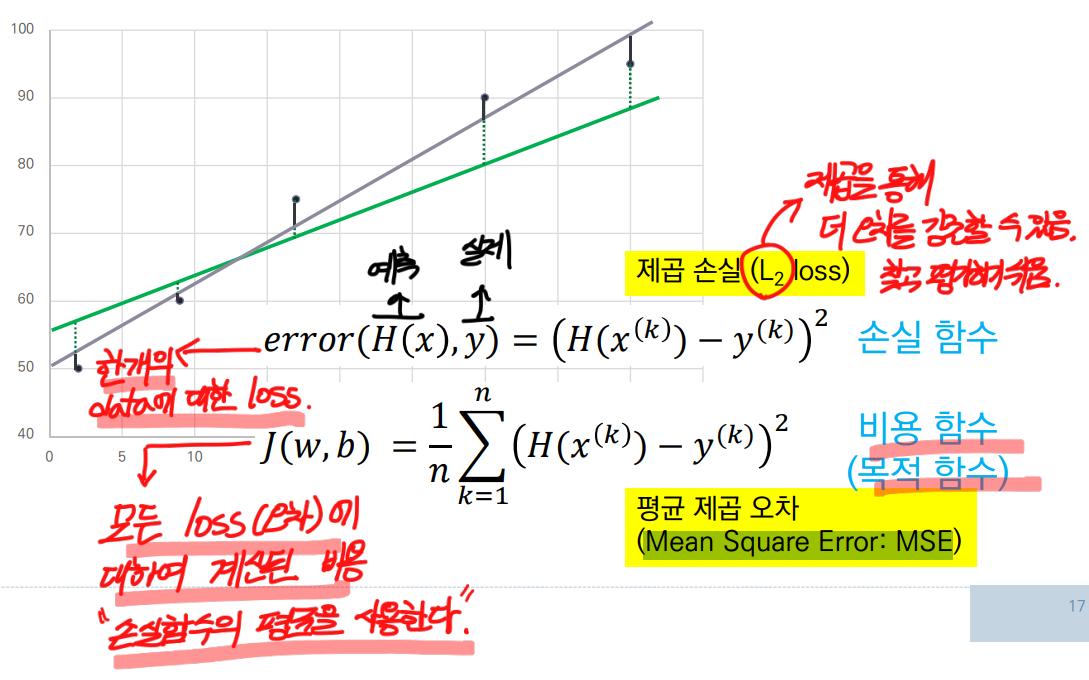
🎯 손실함수(Loss Function)와 비용함수(Cost function)

손실함수? 비용함수?

손실함수란 한 개의 data에 대한 loss(오차)

비용함수란 모든 data에 대한 loss(오차)의 평균
🎈 쉽게 말해 비용함수란, 손실함수를 전부 더해서 평균을 낸 것
이를 MSE(Mean Square Error: 평균 제곱오차)라고 한다.

오차를 구하는 방법
$(H(x^{(k)})$ - $y^{(k)})^2$ = 예측 값 = 추정한 직선의 결과 y값 = $\hat y$ ) - 실제 데이터의 결과 $y$ 값 계산 후 제곱
🎈 ex.) 실제 데이터 (2, 4)라는 값이 있는 경우, 추정 직선 $y=wx+b$ 에 2를 대입하여 나온 y 값이 예측값( $\hat y$ )이 되고, 실제 데이터의 결과값 $y$ 는 4이다. 이를 빼주고 제곱한다.

평균 제곱 오차(MSE : Mean Square Error)를 Cost function으로 사용한다

🎯 손실함수, 비용함수의 목적은?

자 마지막으로, 깔끔하게 다시 정리해보자.
자, Linear regression이란 선형 회귀를 통해 최적의 Model을 추정하는 과정이다.
손실함수는 데이터와 예측 함수 간 오차를 기반으로 유도된다.
비용함수는 이러한 손실함수를 기반으로 유도된다.
따라서, 비용함수 $J(w,b)$ 의 $w, b$ 값이 최소가 된다면 "모든 data에 대한 오차를 최소화"하는 것이라고 할 수 있다.