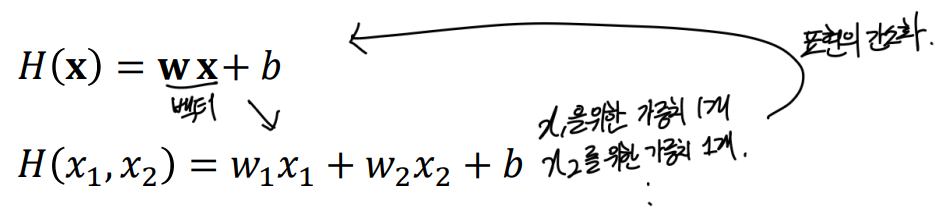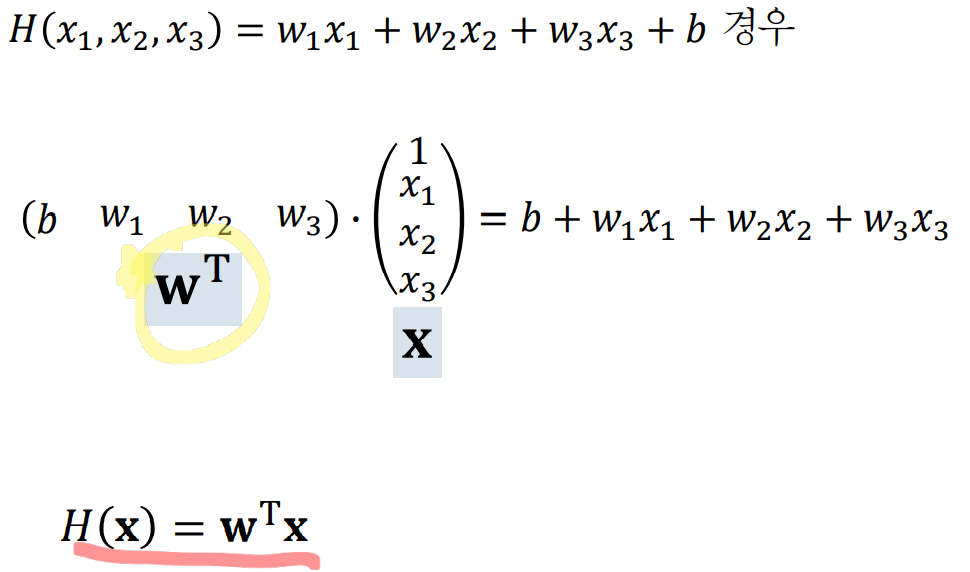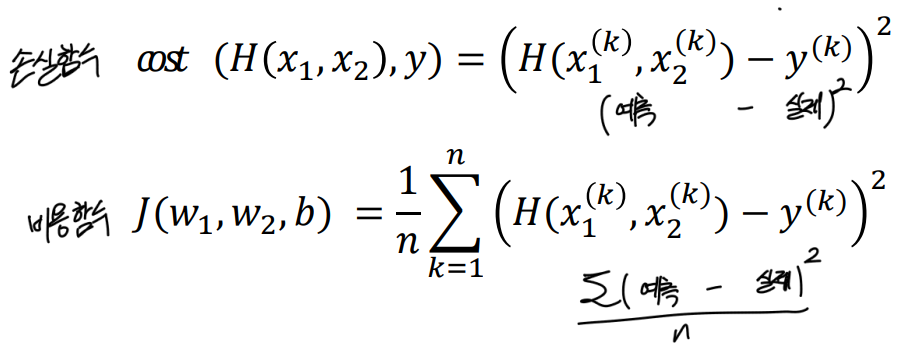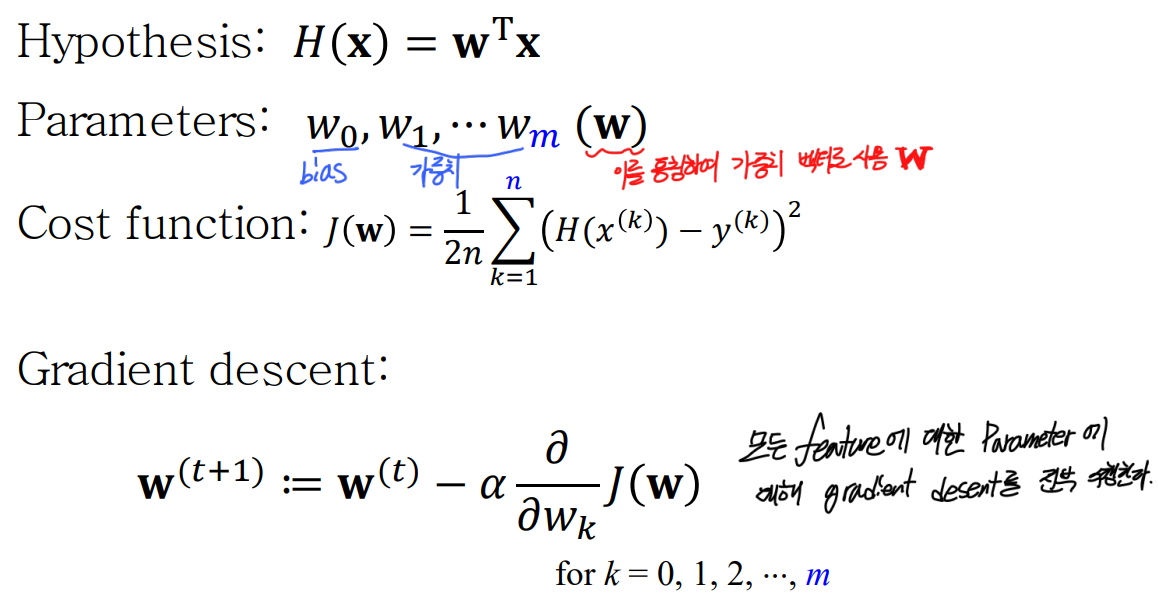🚩딥러닝 기초 - part07. Multi-Variate Linear Regression (다중 선형 회귀)

🟢 Introduction

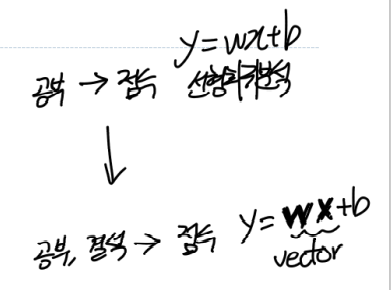
현재까지는 $y=wx+b$ 즉 $x$ 한 가지 독립변수를 통해, 종속변수 $y$를 구하였다.

• (bias는 input 데이터가 나타내는 feature가 아닌 적절한 조정에 사용되는 단순한 파라미터이므로 제외)

예를들어, 학생의 공부시간 이라는 x 데이터 하나만으로 과목점수 y를 지금까지 예측한 것이다.

이것만으로 충분히 과목점수 y를 잘 예측할 수 있을까?

당연히 공부시간, 결석일, 집중도, 컨디션.. 등 많은 요소 즉, feature 들을 포함 한다면 더 정확한 과목점수 y를 예측할 수 있을 것이다.

따라서 이번 part07에서는 이러한 feature값이 여러개인 Multi-Variate Linear Regression (다중 선형 회귀) 를 알아보자!

📊 다중 선형 회귀

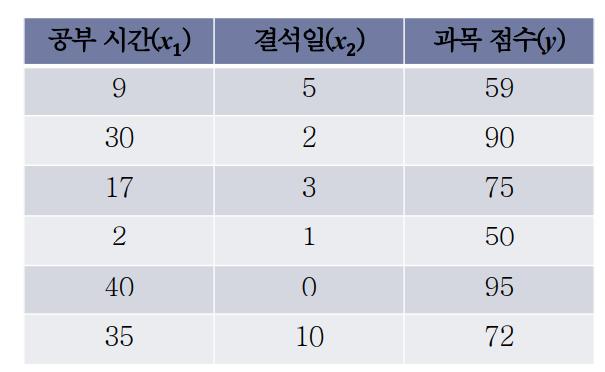
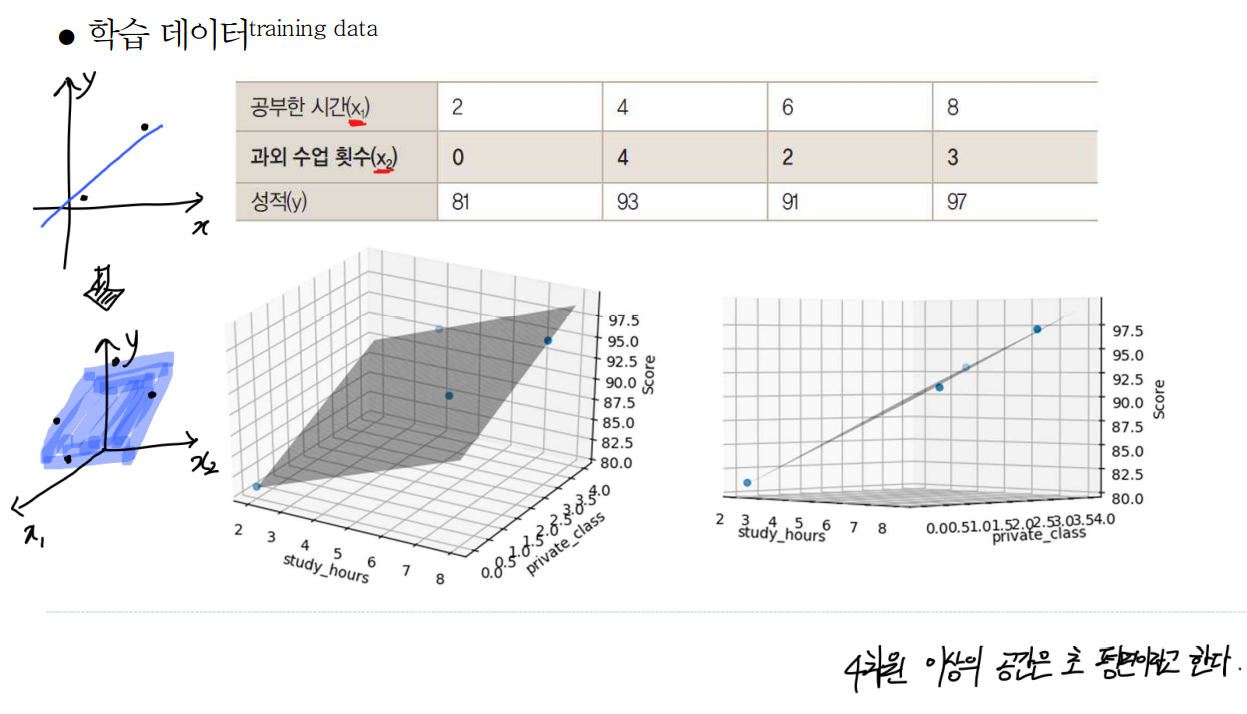
공부시간, 결석일 2가지의 feautre을 통해 과목점수 y를 예측하는 모델을 만든다고 가정하자.

• 이와 같은 샘플 데이터(학습 데이터)를 활용하여 우리는 다중 선형 회귀를 수행하고, 적절한 예측 모델을 만드는 것이 목적이다.
• 그저 변수가 하나 추가되었을 뿐, 선형 회귀와 동일하다 쉽게 생각하자!
  

♍ 수식

수식은 다음과 같다.

• 예측에 있어 하나의 feature가 있을 때는 단순히 변수로 쓰나, 2개이상의 변수가 사용될 때는 이들을 묶어 벡터화 시키고 $WX$ 대문자로 표현한다.
  
• $WX$를 뜯어보면 별 거 없다.
  단순히 길게 쓰기 싫어서 줄인 거라 생각하면 된다.
  
  feture $x1$, $x2$에는 각각의 weight가 붙는다. (조정될 값이니까 당연)

✅ 벡터를 사용한 표현의 단순화

벡터화가 어떻게 이루어 졌길래, 저 식이 저식이랑 같은 것인지 궁금하지 않은가?

그렇다 나도 안 궁금하다. 그래도 feautre가 많아지는대로, 그걸 길게 끝도 없이 쓸 수는 없다.
그렇기에 알아야 할 것이다. 알아두도록 하자.

1. b를 생략하고 벡터화

쉽게 이해하기 위해 b를 생략하고 생각해보자
weight와 bias를 를 각각 묶어 행렬 곱 형태와 유사하게 나타낼 수 있다. 이는 연산결과 동일하다는 것을 보인다.
이후 이러한 부분을 Bold체로 W, X로 표현하면, 이것이 벡터화이다.

2. bias를 포함시켜서 벡터화를 한다면?

별반 다를 거 없다!

bias또한 갱신되는 파라미터이므로 $W$의 행렬과 함께 묶고,
feature augmentation을 통해 상수항 1을 feature을 나타내는 $x_ n$ 행렬에 추가한다.

• feature augmentation
  쉽게 생각해서, 연산을 위해서는 bias랑 짝을 맞춰야 하므로, 단순히 feature 부분에 1을 추가한 것이다.

💥 문제점 - 벡터는 기본적으로 열벡터

위에 그림들이 표현을 위해서 저렇게 했지만...사실..벡터는 기본적으로 열 벡터이다..

• 열벡터와 행벡터
  

따라서 (1x3) x (3x1)가 아닌 실제로는 (3x1) x (3x1)의 연산이므로 이는 이루어 질 수 없다. (행렬 곱의 개념)

그렇기에 행렬을 $W^T$ 즉 Transpose 해주게 되면 해결된다.

• transpose의 예
• 이렇게 표기함으로써 해결되었다!
  

👨‍💼 여러 샘플에 대한 표현의 단순화

자 앞선 예시들은 하나의 샘플 즉, 사람 한명의 x1(공부시간), x2(결석), x3(고액 과외 횟수)의 freature에 대해서 식을 세웠다.

근데 샘플(사람) data는 당연히 1개가 아닌 수십 수백개가 될 수있다. (학습을 data 하나로 할 수는 없지 않은가?)

그럼 어떻게 나타내면 될까?

각 사람의 feature 값들 " x1(공부시간), x2(결석), x3(고액 과외 횟수)" 의 종류는 모든 사람이 동일하므로, weight의 경우 따로 해줄 이유는 없다.

각 feature 별 하나씩만 있으면 되기 때문이다.

따라서 변경되는 부분은 각 사람마다 다른 x1(공부시간), x2(결석), x3(고액 과외 횟수)" 의 값 이다.

• 핵심만 보자.
  100개의 샘플(사람)이 있는 경우 4x1 크기의 $X$ 가 100명의 모든 feature 값을 표현해야하므로 4x100 크기가 된다. 끝
  

📉 손실함수와 비용함수

이 또한 최소한의 오차를 가지는 모델을 만드는 것이 목적이므로, 오차를 이용하여 최적의 모델을 만든다.

이를 위해서는 다중선형 회귀또한 선형회귀와 동일하게 손실/비용 함수가 필요하다.

• 하나의 data에 대해서 Loss를 결정하는 손실함수
• 모든 data에 대해서 Loss의 평균을 구하는 비용함수
  

🎢 Multi-Variate Gradient Descent

최소의 Cost를 가지는 선형 회귀식을 만들기 위한 Gradient Descent를 수행!.

이전 하나의 feature에 대하여 Gradeint Descent를 수행하기 위해서는 $w$편미분, $b$편미분을 통해서 우리는 weight, bias를 각각 갱신했다.

이번에는 feature값이 N개(2 이상)이고, 이에따른 weight또한 같은 N개(2 이상)가 되는 Multi-Variate한 상황이다.

어떻게 해야할까?

별 수 있나..다해야지

• 각 $w _1, w _1, w _1, ....w _N$ 에 대해서 다 편미분을 따로 한 뒤, 각 feaute에 대한 weight를 업데이트 해줘야한다..

모든 weight에 대해서 gradient desent(경사하강법)를 수행한다.

📉 Multi-Variate 일때의 그래프

• feature가 1개일때는 2차원 평면에 표현했다.
• 2개로 늘어났으니 3차원 평면에 표현하게 된다.
  
• 4차원 이상은 초평면이라고 한다.

이것으로 Multi-Variate Linear Regression (다중 선형 회귀) 를 마친다.