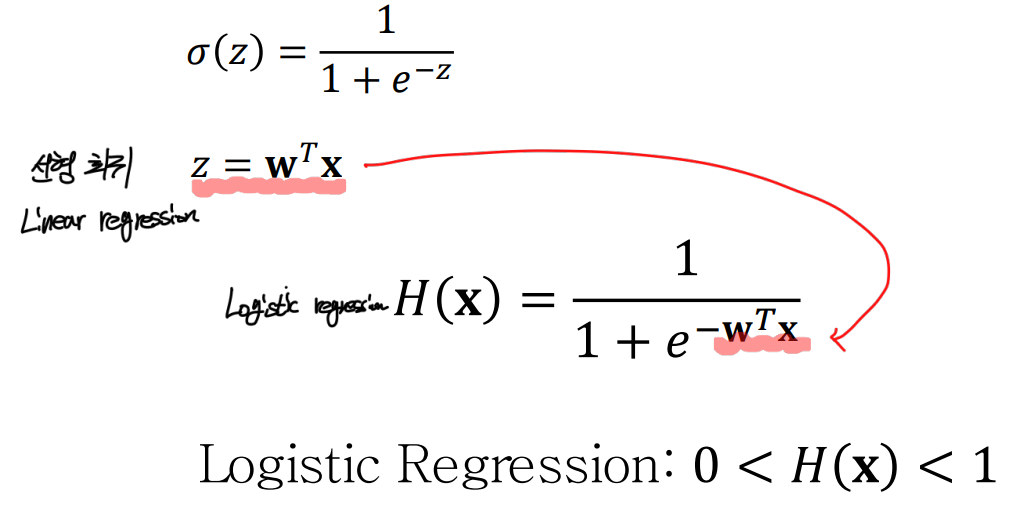🚩딥러닝 기초 - part08. Logistic Regression 로지스틱 회귀 분석 (feat. Use sigmoid function)

Introduction

이전까지는 선형회귀로 예측을 수행하는 모델을 만드는 방법을 공부해 보았다.

이번에는 참과 거짓, YES와 NO등 2진값으로 분류하는 모델을 만들어보도록 한다.

• 이진분류의 예
  

+) 🎈 글을 들어가기 전, 참고사항

• 참 == true == positive / 거짓 == false == negative
  이들을 글을쓰다보니 계속 혼동해서 사용하게 되나, 이진분류이므로 이들은 다 같은 말이구나 생각하면 된다.

What is Logistic?

이전에 공부한 Linear Regression을 다시 생각해보자.
Linear은 즉 그래프의 개형이 1차 함수로써 선형을 의미했다. (직선)

그럼 Rogistic은 어떤 그래프의 개형을 가질까?

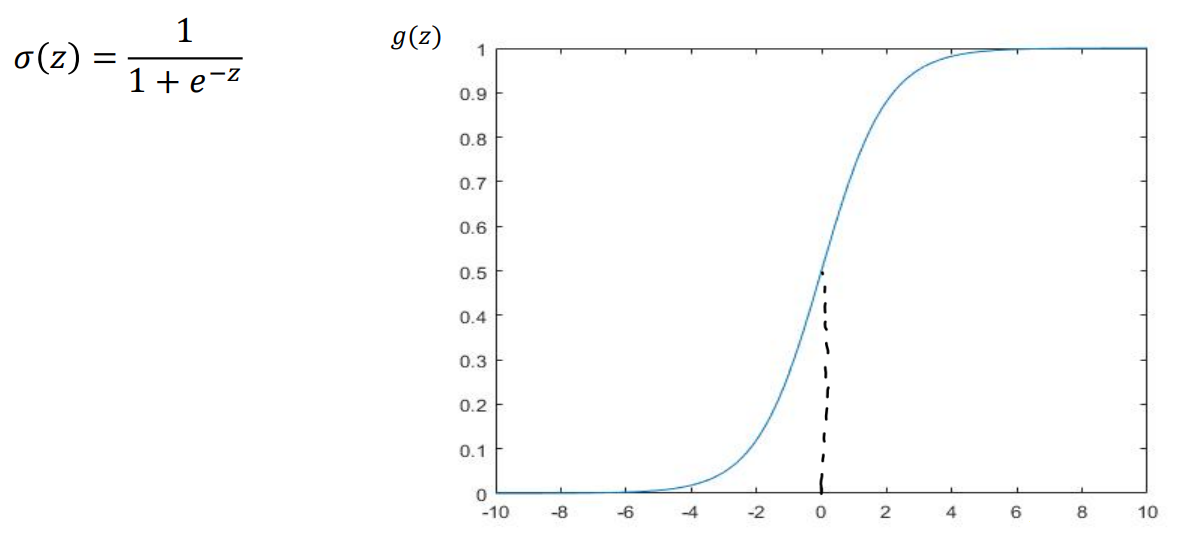
미리 보자면 Sigmoid 함수 그래프를 사용한다.

• 시그모이드 함수
  그렇다. 아무리봐도 직선(Linear)은 아닌 것 같다... 그렇기에 Rogistic이라 부른다.

그럼 Logistic Rregression이란 무엇일까?

Logistic Regression 이란?

Introduction에서 이미 답을 말했지만, 참과 거짓을 분류하기 위한 과정이다.
이러한 로지스틱 회귀를 통해서 우리는 이진 분류하는 모델을 만든다.

• 이진 분류의 최적 모델을 만드는 과정이 Logistic Regression이고, 이를 통해 만들어 진 것이 Model이다.

자 이제 이러한 함수를 사용하는 이유를 알아보도록 하자.

Why use Logistic(Sigmoid)?

그냥 쉽게 이진분류에도 Linear를 그대로 사용하면 안 되는가?

그래. 당연히 안되니까 Rogistic을 쓰는 것이다.
다음 예시를 보자.

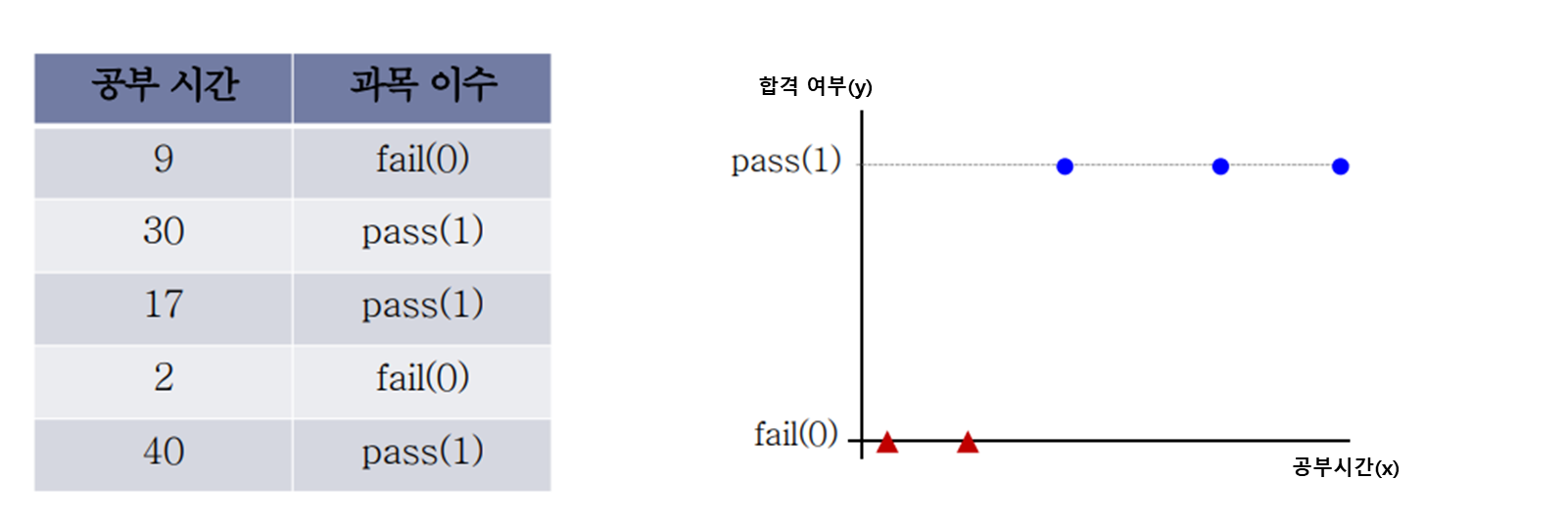
공부시간에 따른 과목이수 여부(fail, pass)두 가지를 판단하는 분류기를 만든다고 가정하자.

학습을 시키기 위한 입력 데이터는 왼쪽과 같고, 이를 좌표 평면상에 표현한다면 오른쪽과 같을 것이다.

이들을 잘 표현할 수 있는 최적의 직선 (Linear)을 그어볼 수 있겠는가?

어찌저찌 선은 그엇다만...잘 표현한다고 할 수 있을까?

• 이진 분류이므로 0또는 1이라는 값만 나오도록 해야한다. 따라서 결과는 중간값인 0.5를 기준으로 분류한다.
  (즉, 결과($y$)는 중간이 없다)
• $y=0.03x+0.02$의 선형 모델을 하나 만들었고, 공부시간($x$)를 모델에 대입했을 때, 해당 값이 0.5이상이면 합격(1)로 0.5미만이면 불합격(0)으로 $y$(합격 여부)를 결정한다. (결과($y$)는 중간이 없다)

공부시간 $x$(17)을 $y=0.03x+0.02$의 선형 모델에 적용했을 때, 아슬아슬하게 0.53의 값으로 0.5이상의 값이 나왔다. 데이터를 잘 반영하는 것 같이 보인다!

Linear Regression 사용의 문제점 1

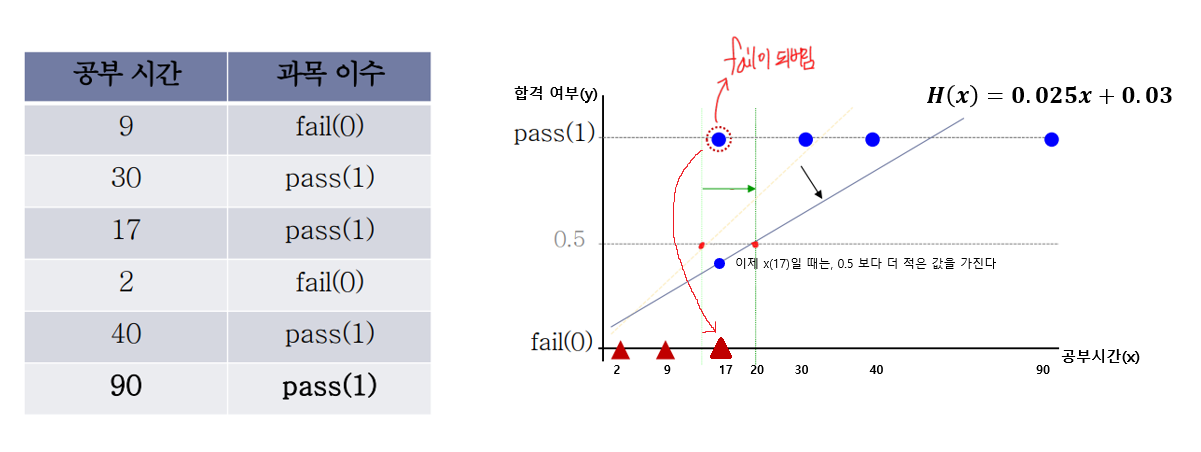
하지만, 여기에 새로운 데이터 샘플이 하나 더 추가된다고 생각해보자. 그럼 우리는 이러한 추가된 데이터를 반영해야 하므로 그래프를 약간 update해 주어야할 것이다. 이러한 update는 Linear Regression의 과정을 거친다.

• 17시간이면 합격을 했는데, 이제는 fail이 되어야 한다??

그림에서 보듯, 공부시간 $x$(17)을 update된 $y=0.025x+0.03$의 선형 모델에 적용했을 때, 이제는 0.455의 값으로 0.5미만의 값이 나온다.

실제로 17시간을 공부하고 합격한 학생이지만, 저 그래프대로 생각한다면 사실상 불합격이라는 얘기다.
이렇게 Linear을 사용할 경우 참 억울한 상황이 연출되게 된다..o(TヘTo) (이는 제대로 된 학습이라 볼 수 없다)

Linear Regression 사용의 문제점 2

데이터의 반영또한 문제지만 또 다른 문제점이 있다.

선형 함수라는 것은 y축의 양과 음의 방향으로 사실상 무한하게 이어져 있다는 점이다. (제한이 없다)
y = 1x 라는 함수가 있다면, x에 100을 넣으면, y는 100이되고, 1000을 넣으면 1000까지... y의 범위가 무궁무진하다.

그래서 이게 무슨 문제인가?

y는 0또는 1만을 가져야하는 이진분류에서 음의 무한대, 양의 무한대로 출력값이 나올 수 있다는 것은 출력의 범위가 너무나 광범위 해진다는 것이고 threshold 즉, 어디를 기준으로 이수, 불이수로 해야하는지 임계값의 지정하는 것 또한 너무나 어렵게 된다.

따라서 Logistic Function(Sigmoid Function)을 사용하는 것이다!

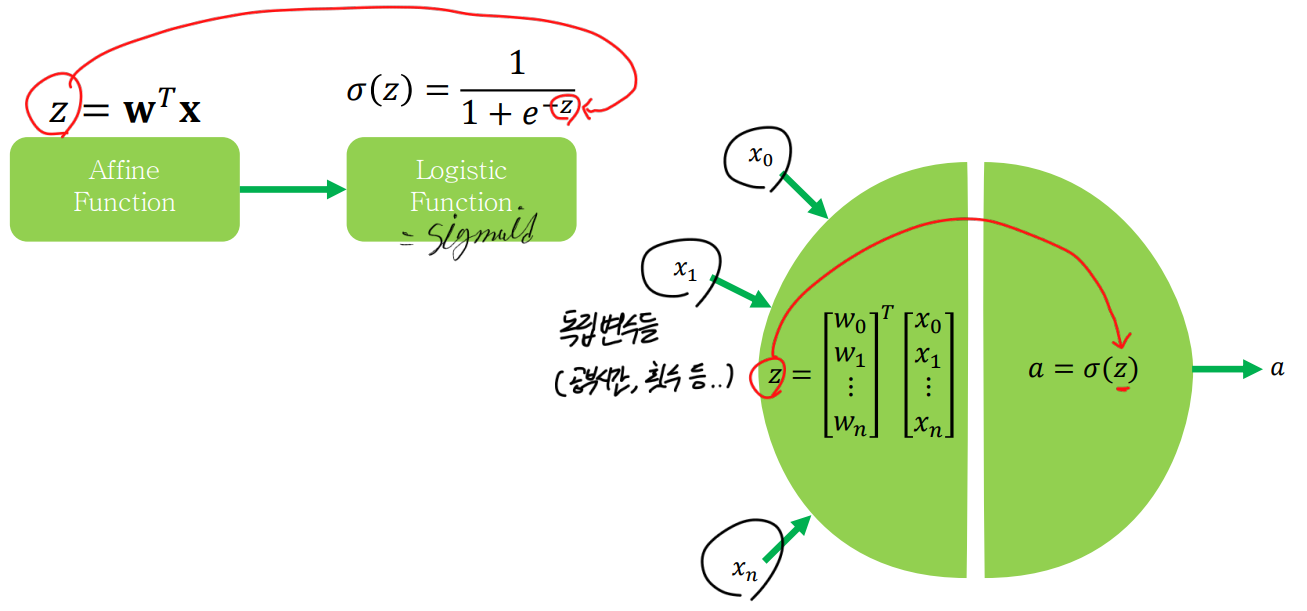
Logistic Regression 함수

• 함수 및 그래프의 개형
• (결과 값 $\sigma(z)$가 0 과 1 사이의 값을 가진다.)
  

• 수식 (선형회귀 수식 $Z$를 그대로 분자의 자연상수($e$)의 지수 값으로 사용한다.)
  이를 통해 출력(예측값)이 0<$H(x)$< 1사이에 위치하도록 사용할 수 있다!

  🎈 참고

  • 이러한 Logistic Regression의 ($Z$)로 들어가는 선형회귀 수식을 Affine Function 이라고한다.
    

Logistic Regression (Sigmoid 함수)의 개형

• Weight와 Bias에 따른 개형을 살펴보록하자. 수식은 다음과 같다.

  $H(x)=$ $1 \over 1+e^{-(wx+b)}$

• 식에서의 $W^TX$ 즉, $(Z)$를 풀어서 썼다.

  

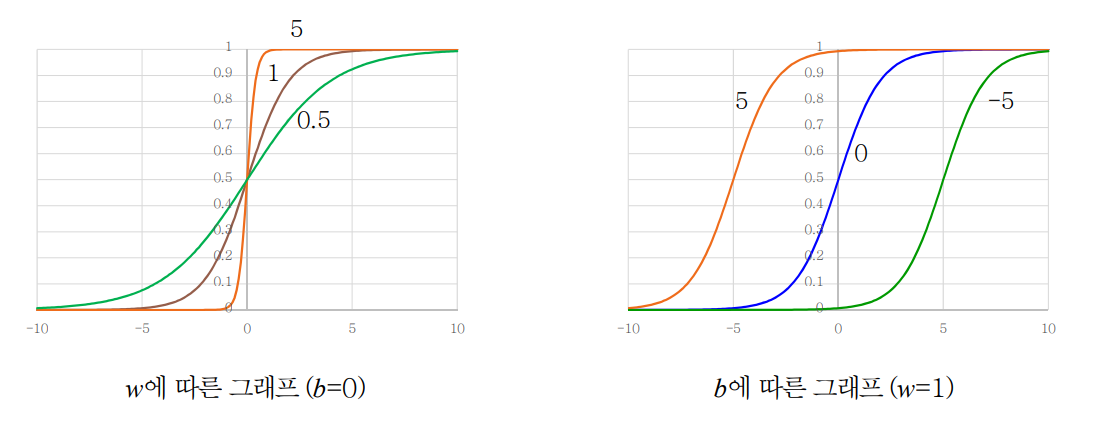
• w가 작아질수록 점점 각도가 낮아져 느슨한 형태의 sigmoid함수가 되며, 오차가 증가하게 된다.
  반대로 w가 커질수록 오차는 감소하게 된다.

• b는 값이 너무 커지거나, 너무 작아지는 경우 오차가 증가하게 된다.

Cost function과 Loss function

기존에 공부했던 Cost function은 평균제곱오차를 사용했다.

• 평균 제곱 오차
  

이 식을 Linear한 즉, 일차방정식 $H(x) = W^TX$ 대해서 적용한다면 다음과 같은 오차를 나타내는 Cost Function이 그려진다.

• 일차방정식(직선)에 대한 평균제곱오차의 그래프
  이 부분이 잘 이해가 되지 않는다면 다시 part06 - 경사하강법(Linear 예제)를 읽어보면 된다.

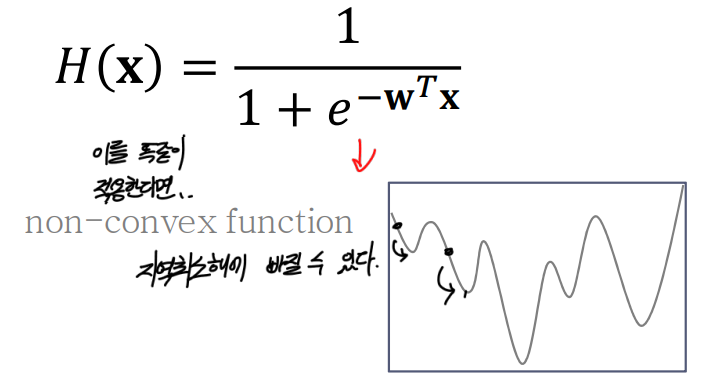
하지만, 이를 Linear하지않은, Sigmoid함수가 $H(X)$로 평균제곱오차(MSE)의 식에 들어가게되면 Cost Function은 어떻게 나올까?

이러한 그래프가 나온다!

• Sigmoid에 대한 평균제곱오차의 그래프(예시)
  

평균제곱오차(MSE) 사용의 문제점

하지만, 이는 경사하강법을 수행하다보면 오차의 시작하는 위치에 따라서 위 그림과 같이 지역최소해에 빠질 수 있다.

지역최소해 : 실제 최소 오차는 저~아래 있지만, 다른 굴곡의 끝 부분을 최소 오차라고 생각하게 되는 것.

따라서, 우리는 Sigmoid를 잘 반영할 수 있는 새로운 오차 함수를 만들어야한다.

MSE야 잘가! 👋

로그 함수

새로운 오차 함수를 만들기 위해서 시그모이드 함수를 다시 살펴보자.

시그모이드 함수의 특징은 y값이 0과 1사이라는 점이다.

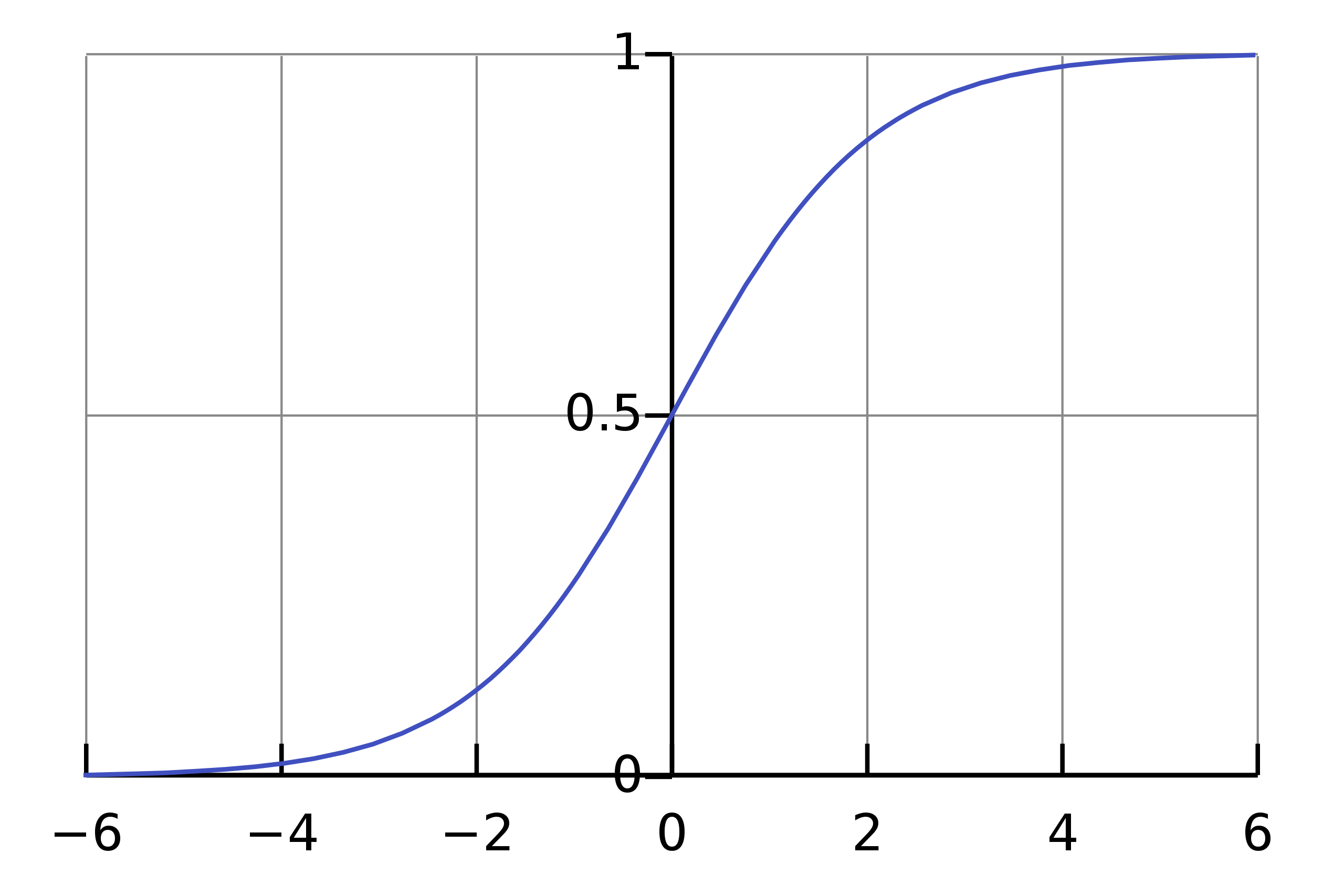
즉, 실제 값(결과$y$)이 1(true)일 때, 0(false)에 가까워 질수록 오차가 증가할 것이고,
반대로 실제 값(결과$y$)이 0(false)일 때, 1(true)에 가까워 질수록 오차가 증가할 것이다.

이 특징을 잘 표현할 수 있는 방법이 무엇일까?

바로 로그함수!

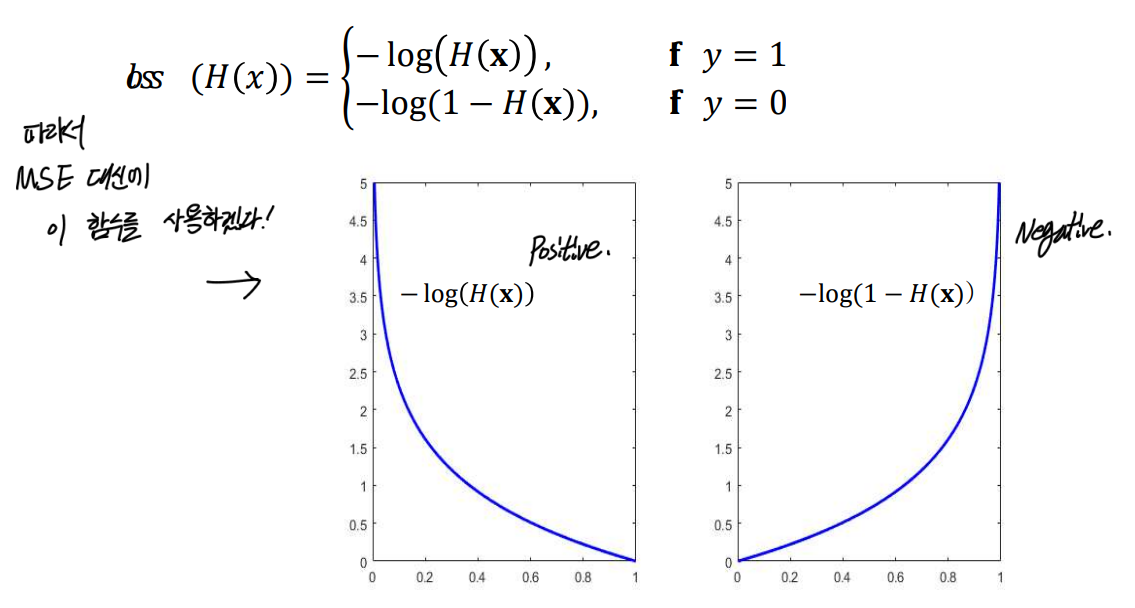
로그함수로 Cost function(비용 함수)를 나타내면 다음과 같다.
참일때와 거짓일 때를 따로 분리해서 그려진다.

• Convex logistic regression cost function
  
• 실제 데이터의 값이 참(1)인 경우 (좌) : 거짓(0)의 값에 $x$의 값이 가까워질수록 오차(y)의 값은 증가한다. (반대로 참(1)에 가까워지면 오차가 감소)
• 실제 데이터의 값이 거짓(0)인 경우 (우) : 참(1)의 값에 $x$의 값이 가까워질수록 오차(y)의 값은 증가한다. (반대로 거짓(0)에 가까워지면 오차가 감소)

어떤가? 로그로 표현하니 아까 말했던 sigmoid의 특징을 잘 반영하지 않았는가?

• 방금봤던 특징

(최종) Cost function for logistic regression

참, 거짓 두개로 분리해서 Cost function을 사용하기에는 여간 불편한 일이 아니다.
따라서 해당 함수 2개를 참/거짓 둘 다 반영할 수 있도록 합쳐보도록 하자.

합치면 다음과 같이 된다.

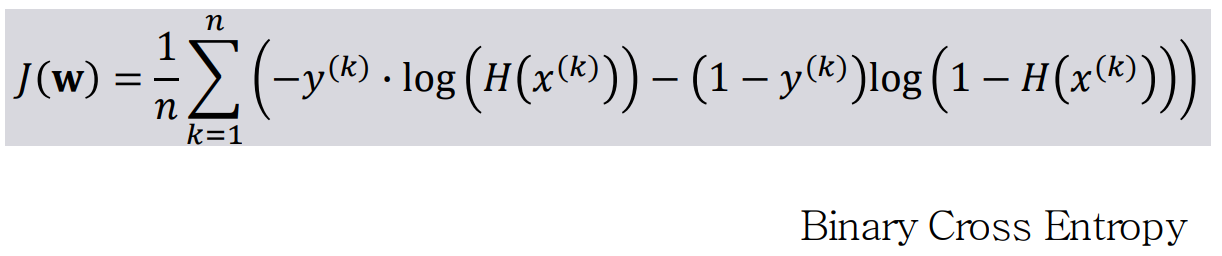
이렇게 합쳐진 cost function을 Binary Cross Entrop 라고 부른다.

Gradient Descent 과정

새로운 cost function(Binary Cross Entrop)을 얻었으니 이제, Gradient Dscent과정을 수행해서 최소의 오차를 구해보자!

Gradient Descent를 어떻게 수행 했는가?
바로 확인해보도록 하자.

1. cost function을 현재($w,b$)를 기준으로 각각 편미분
2. 미분을 통해 얻은 (기울기 값 x lr)를 기존 $w, b$에서 빼준다.
   
   경사하강법이므로, 식이 조금 복잡해졌을 뿐. 기존 Linear와 경사하강법을 하던 방식이 동일하다.

최종 정리

마지막으로 로지스틱 회귀분석의 과정을 최종적으로 정리해보고 끝내도록 하자.

1. 선형 회귀에서 정의되는 일차방정식을 Affine function으로 활용 $Z = W^TX$
2. Logistic function을 정의 (sigmoid 함수의 $Z$값에 Affine function $W^TX$를 넣음)
3. 로지스틱 회귀분석에 맞는 Cost Function인 Cross Entropy Loss(BCE)를 정의
4. BCE를 편미분($w, b$ 각각)한 값에 적절한 lr를 곱해 빼줌으로 써, Gradient Desent를 수행한다.

고생했다! 내가!