Transformer

• 구글에서 공개한 "Attention is all you need" 논문에서 처음으로 공개된 구조
• Attention 기반
• 순환구조 때문에 오래걸리는 RNN, seq2seq의 단점을 보완
• BRET, GPT-3등의 언어 모형에서 사용
• 컴퓨터 비전 등 다른 분야에서도 강력한 도구로 사용중

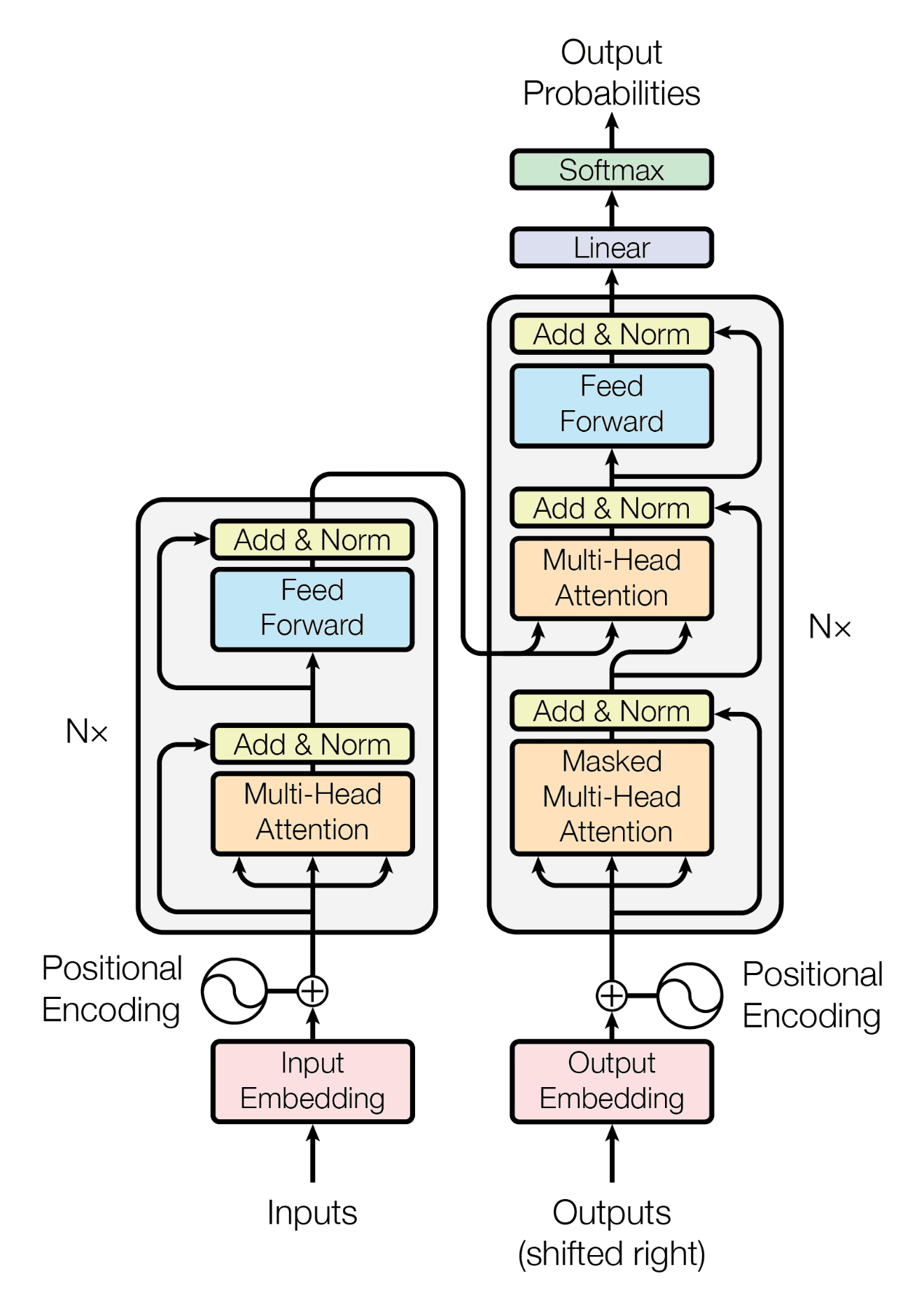
Transformer 구성 요소

• Multihead Attention
• Add & Norm
• Feed Forward
• Masked Multihead Attention
• Positional Encoding
• Linear
• Softmax

Transformer 구조

• 크게 인코더와 디코더로 나눈다.

인코더

• Multihead Attention과 Feed Forward로 이루어진 층이 N번 반복된다.

디코더

• Masked Multihead Attention과 Multihead Attention, Feed Forward로 이루어진 층이 N번 반복

• 디코더를 통과하여 나온 결과는 차원을 맞추기 위해 Linear(FNN 신경망)을 한번 통과한 후 softmax를 통과

• 인코더와 디코더에 입력될 때에는 Positional Encoding이라는 것을 더한다. 이로 인해 순환구조가 아니라도 위치를 인지할 수 있다.

• Add&Norm은 Residual Connection과 Layer Normalization을 의미함

Transformer를 알기전에 알아야 할 용어들

1. Batch Normalization

• 입력 데이터를 정규화 하는 것은 학습 속도 증가 및 정확한 학습에 필수적이다.
• 하지만 처음 입력을 정규화를 했다고 해서 dense, convolution, Relu, Softmax등 수많은 Layer를 거치고 나서도 정규화가 유지될 지는 확실하지 않다.
• 실제로 층이 깊어질수록 입력 데이터를 정규화한 효과는 없어진다.
  -> 층을 거칠때 마다 정규화 시켜준다.
  

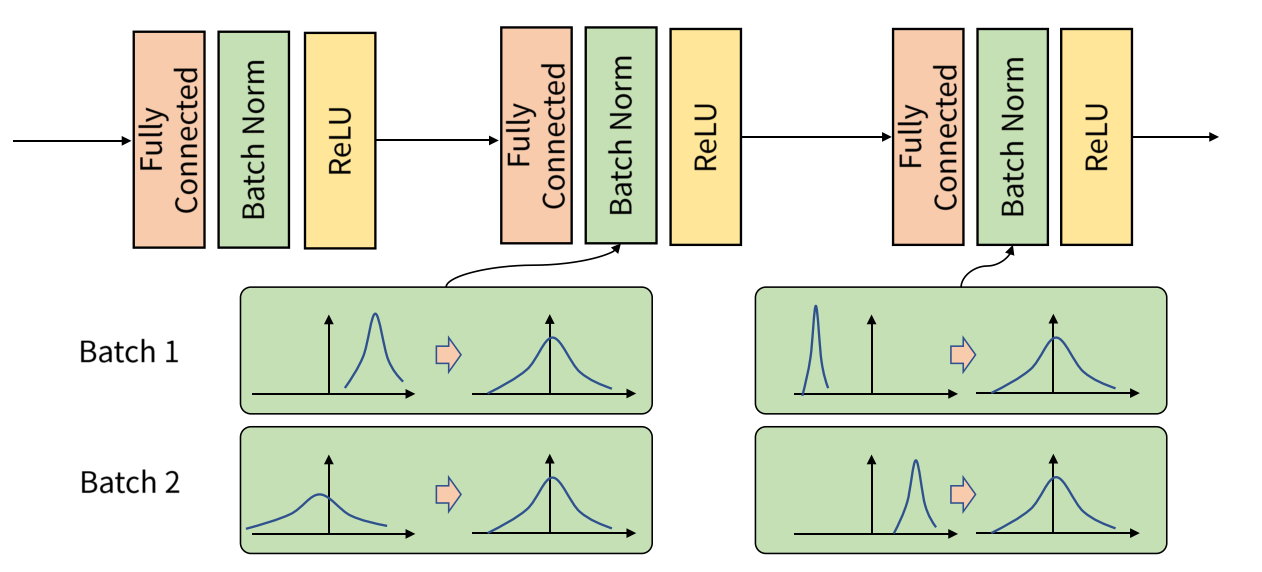
Batch Normalization

• Batch Normalization은 Layer를 통과한 이후에 정규화를 적용하여 모든 층이 정규화된 데이터를 입력으로 받을 수 있게 해준다.
• 테스트 시에는 training data에서 학습한 평균과 표준편차 값을 사용하여 정규화 한다.
  

단점

• batch의 크기가 어느 정도 커져야 한다.
• 테스트용 데이터의 차원이 트레이닝 데이터보다 커지면 사용이 불가능(NLP에서 사용이 부적절)

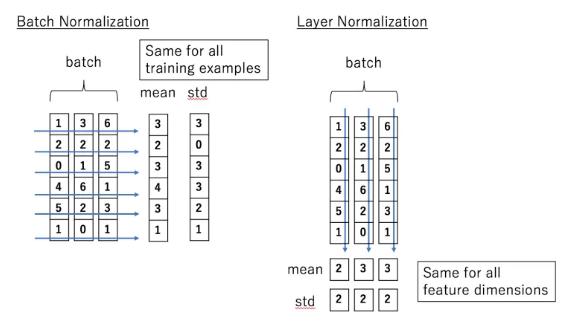
2. Linear Normalization
   데이터셋 내의 데이터별로 모든 차원에 대한 평균과 표준편차를 구한다.

• 데이터마다 차원의 개수가 바뀌는 것에 무관하게 적용 가능하다.
• NLP에서 사용하기 적합하다.
• 시퀀스가 길어져도 정교화를 적용 할 수 있다.
  

3. Residual Connection
   

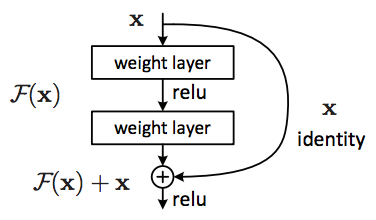
• H(x) = F(x) + x
• F(x)의 결과에 대한 출력이 0에 가까운 값이라도 H와 x에 대한 기울기는 1 근처로 보장됨
  -> gradient vanishing에 대한 해결책

Scaled Dot Product Attention

• Transformer의 핵심은 '디코더의 hidden state를 어떻게 정확하게, 효율적으로 산출할 것인가?'이다.

• 총 3가지 변수를 이용하여 다음 hidden state를 구한다.

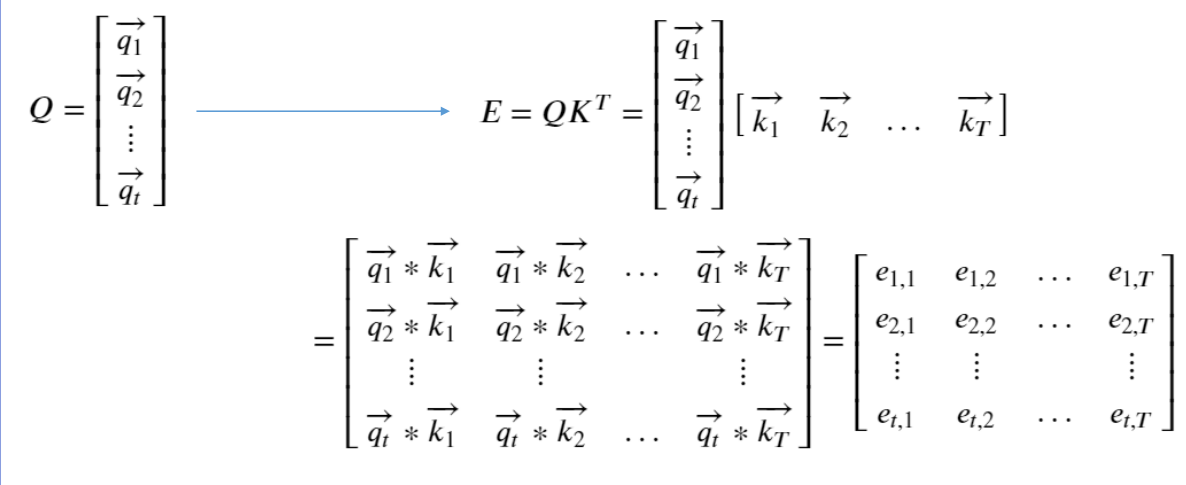
• Q(쿼리) : 직전 디코더의 hidden state -> shape-(t, d)

• K(key) : 인코더 전체의 hidden state -> shape-(T, d)

• V(value) : 인코더 전체의 hidden state -> shape-(T, d)

• 총 attention score를 Q와 K의 내적(dot product)을 통해 계산한다.
  

• attention score에 softmax를 취해 attention weight를 계산해 주려고 한다.

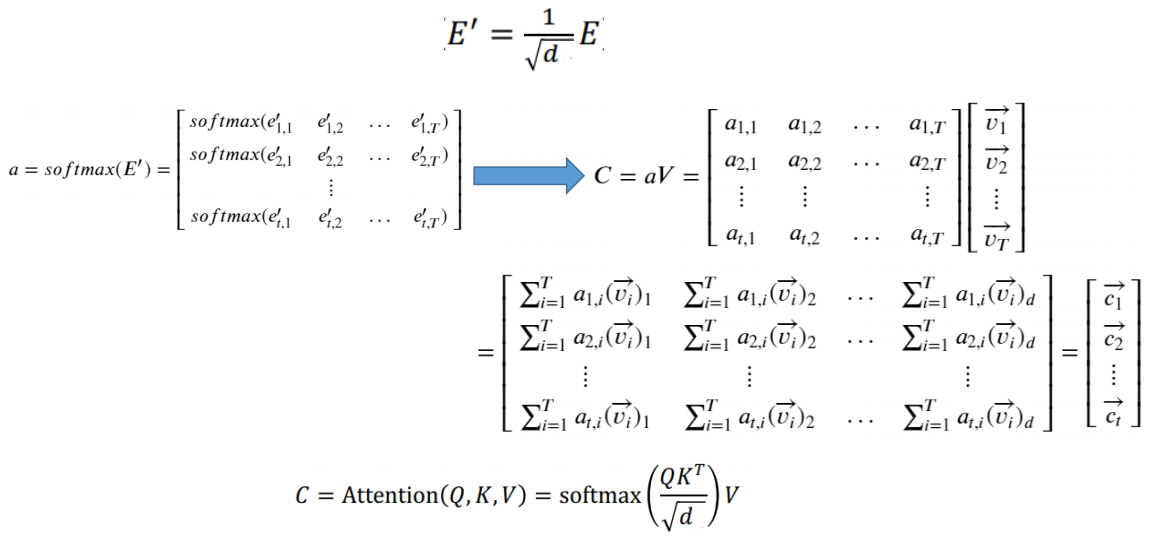
• 그 전에, 내적값이 너무 커져서 0에 가까운 값이 되는 것을 방지하기 위해서 attention score를 root(d)로 나누어 준다.
  

Multihead Attention

• Scaled Dot Product Attention의 경우 연산 과정이 직렬적으로 이어져 있기 때문에 병렬화가 불가능 하다. 이론 인해 시간이 너무 오래 걸린다.

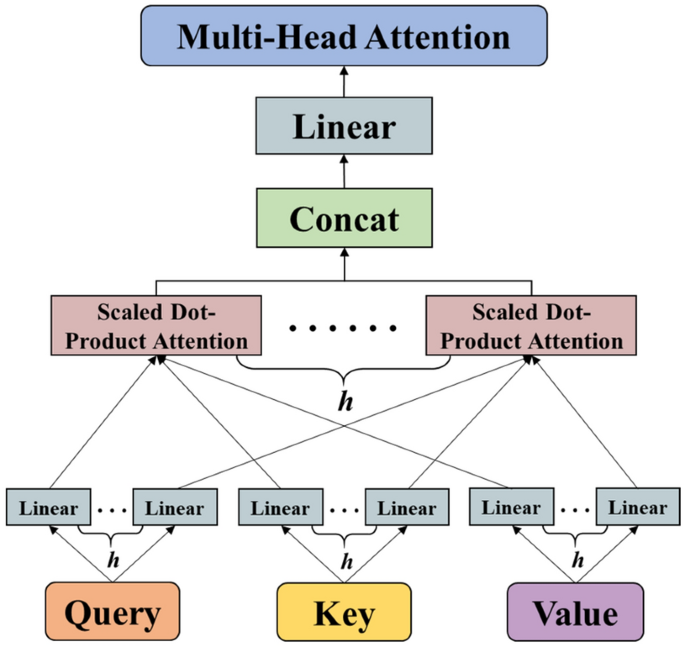
• 이를 해결한 것이 Multihead Attention

• 하나의 Attention연산을 h개로 쪼개어 동시에 진행하는 방법

• 앞에서 살펴본 Attention(Q,K,V)함수 하나하나를 attention head라고 부른다.

• 각 attention head마다 다른 feature가 학습되도록 한다.

• 각각의 attention head를 병렬적으로 연산한다.
  

• i번째 attention head(i = 1,2,...,h)에 각각 앞에서 구한 Q(i), K(i), V(i)를 넣어서 C(i) = Attention(Q(i), K(i), V(i)) = softmax(Q(i)K(i)T/root(dk))V(i)를 계산하여 (t, dv)모양의 행렬 h개를 얻는다. (이때 dk = dv = [d/h]) 이를 모두 이어 붙이면 차원이 (t,h[d/h])인 하나의 행렬 C를 얻는다.

• Multihead Attention을 통해 나온 결과는 단일 attention head를 사용하여 나왔던 결과의 차원 (t,d)와 같아야 한다. 따라서 Wo = R^(h[d/h]Xd)를 곱하여 최종 출력 Cout = CWo를 얻는다.

• 지금까지의 과정은 하나의 sequence(text분야에서는 하나의 문장을 의미)를 처리하는 과정을 배운 것이다.

• 우리는 수많은 sequence 즉, 여러 문장을 학습시켜야 한다.

• 따라서 하나의 문장을 의미하는 Batch를 한번에 처리할 수 있어야 한다. 즉, N개의 sequence로 이루어진 Batch를 한번에 처리할 것이다.
  

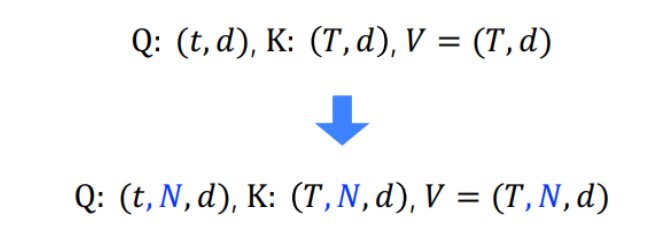
• 마찬가지로 dot product로 attention score 계산 후 softmax 적용하여 attention weight 얻는 과정을 거쳐야 한다. 우선 Q와 K를 dot product하여 E를 구한다.

• E = Q' X K' : (t,N,h,dk)X(T,N,h,dk) -> (t,N,h,T)

• N과 h는 행렬 연산을 통해서 변하지 않는다. N은 batch즉, 문장의 개수이고 h는 attention head의 개수이다. 이 둘은 사용자가 지정하는 hyper parameter이다. (즉, N과 h는 계산을 할 때 무시하고 계산해도 된다.)

• 이렇게 얻은 E를 root(dk)로 나눠주고 softmax를 통과하여 attention weight인 α계산 이때 차원은 그대로 (t,N,h,T)
  α = softmax(QK^T/root(dk))

• attention weight와 V를 행렬곱하여 attention head별 context vector를 얻는다.
  C' = αXV' : (t,N,h,T) X (T,N,h,dv) -> (t,N,h,dv)

• attention head별로 얻어진 context vector를 모두 합쳐서, 단일 attention일 때와 같은 차원의 결과가 나오도록 Linear를 한번 통과시킨다.
  C' -> C : (t,N,h,dv) -> (t,N,hdv)
  Cout = CXWo : (t,N,hdv)X(hdv, d) -> (t,N,d)

• dk = dv = [d/h]

masked multihead attention

• transformer의 decoder는 incoder와 다르게 target sequence가 입력되어야 한다.
  -> 답을 예측하기 위해서 학습을 진행하는데 입력으로 답을 넣는거는 이상하다. 근데 왜 target sequence를 넣는건가?
  => teacher forching을 위해서 !!

• NLP는 전통적으로 현재 예측값을 가지고 다음 토큰을 예측하는 구조를 가진다.(순서가 중요)

• 이런 구조면 첫 토큰의 예측이 실패한다면 이후 토큰들은 점점 정답과 멀어지게 된다.

• 즉, 예측이 올바르지 못하면 그 이후의 토큰 예측은 정상적으로 수행되지 못한다. 이를 방지하는 것이 Teacher Forcing
  -> 그럼 Teacher Forcing이 뭔지 알아보자

Teacher Forcing

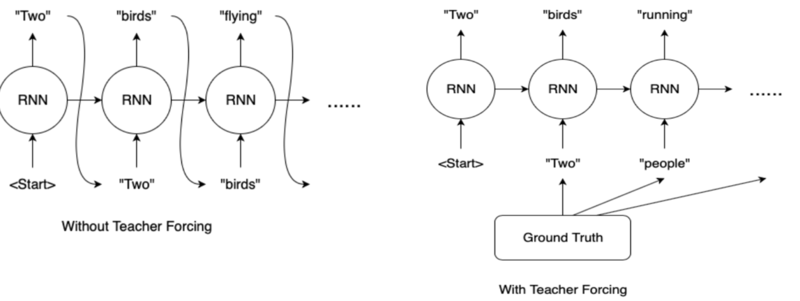
• 잘못된 예측이 있을 경우에 다음 예측에 사용될 입력 값으로 올바른 예측값을 넣는 것이 Teacher Forcing

• Transformer의 decoder에서도 Training과정에서 Teacher Forcing기법을 활용하기 위해 target sequence를 입력해 준다.

• 그런데, 이 과정에서 target sequence의 모든 원소를 그 값 그대로 입력해주면 신경망은 그 값을 그대로 외우게 될 것이다. 이를 방지하기 위해서 입력되는 tagret sequence에 제한을 걸어준다.

• t번째 토큰을 예측하고자 한다면, t+1번째 이후 토큰들에 대한 정보는 알면 안된다. 이를 위해 mask를 attention층을 거친 target sequence에 씌워준다.

masked multihead attention

• 예를 들어 target sequence에 self-attention을 적용한 결과가 다음과 같다면

np.array([[0.1,0.7,0.2],
		  [0.4, 0.2, 0.4],
          [0.1,0.8,0.1]])

• 위 배열의 첫번째 행을 보면, 첫 토큰을 예측할 때 두번째 토큰의 attention값이 0.7로 상당히 많은 부분을 관여하는 것이 보인다. -> 이는 바람직하지 않다.

• 첫 토큰의 경우 첫번째 토큰만이, 두번째 토큰의 경우 첫 토큰과 두번째 토큰의 영향만을 받아야 한다.(즉, 토큰 예측은 현재 토큰과 그 이전의 토큰들만을 가지고 예측을 해야한다.)

• 따라서 다음과 같이 0으로 masking하여 현재 토큰 이후에 나오는 토큰들의 영향을 제거해야 한다.

np.array([[0.1,0,0],
		  [0.4, 0.2, 0],
          [0.1,0.8,0.1]])