메타러너

이상억·2024년 8월 5일
인과추론

인과추론

목록 보기
3/3

메타러너

  • ML Algorithm 활용하여 처치 효과를 추정하는 간단하면서도 강력한 방법론
  • 조건부 평균 처치 효과(CATE, Conditional Average Treatment Effect)를 추정하는 데 주로 사용
  • 실험 대상이 어떻게 처치에 따라 다르게 반응하는지를 식별하는 데 중점

기본 개념

  • 기존 예측 ML Algorithm 활용해 처치효과를 추정하는 간단한 방법

  • ATE 추정에 사용할 수 있지만, 일반적으로 고차원 데이터를 잘 처리 하기 때문에 CATE 추정에 사용

  • 예측 모델을 인과추론에 재활용하는 역할

  • 메타러너는 다양한 머신러닝 알고리즘과 결합하여 사용할 수 있음.

    • 선형 회귀(Linear Regression): 간단한 예측 모델로, 해석이 용이.
    • 부스트 의사결정 트리(Boosted Decision Trees): 고차원 데이터를 잘 처리하며, 강력한 예측 성능을 보임.
    • 신경망(Neural Networks): 복잡한 비선형 관계를 잘 학습 함.
    • 가우스 과정(Gaussian Processes): 확률적 모델로, 예측의 불확실성을 평가할 수 있음.

이산형 처치 메타러너

온라인 소매업체의 마케팅 팀에서 일한다고 가정하고, 목표는 어떤 고객이 마케팅 이메일에 긍정적으로 반응하는지 파악하는 것. 마케팅 이메일은 고객의 소비를 늘릴 잠재력이 있지만, 일부 고객은 이를 선호하지 않을 수 있다. 이를 해결하기 위해, 이메일이 고객의 미래 구매량에 미치는 조건부 평균 처치 효과(CATE)를 추정. 이를 통해 효율적인 이메일 발송 전략을 수립.

import pandas as pd
import numpy as np
data_biased = pd.read_csv("./data/email_obs_data.csv")
data_rnd = pd.read_csv("./data/email_rnd_data.csv")
print(len(data_biased), len(data_rnd)) data_rnd.head()

mkt_emailnext_mnth_pvagetenure...jewelbooksmusic_books_movieshealth
002442661.01.0...1002
10296736.01.0...1022
20117364.00.0...0100
30414174.00.0...0410
404478959.00.0...1121
  • 실험 데이터와 관측 데이터에는 동일한 열
  • 여기서 이메일 발송 여부인 처치변수 mkt_email가 이메일을 받고 한 달 후의 구매 금액인 next_mnth_pv에 미치는 영향을 알아보겠음
  • 이 열 외에도 데이터에는 나이, 첫 구매 이후의 기간, 각 카테고리에서 구매한 금액과 같은 다양한 공변량이 포함
  • 이러한 공변량에 따라 적합시키려는 이질적 처치가 결정

CATE 모델 개발을 간소화하기 위해 처치, 결과, 공변량, 훈련 및 테스트 셋을 저장하는 변수를 생성 할 수 있음, 이를 다 갖추면 대부분의 메타러너를 구성하는 일이 간단해짐

y = "next_mnth_pv"
T = "mkt_email"
X = list(data_rnd.drop(columns=[y, T]).columns)
train, test = data_biased, data_rnd

T 러너

  • 범주형 처치를 다룰 때 첫 번째 시도해 볼 메타러너는 T 러너
  • T 러너는 매우 간단, 잠재적 결과 YiY_i를 추정하기 위해 모든 처치에 대한 하나의 결과 모델 ut(x)u_t(x)를 적합
  • 이진 처치에서는 추정해야 할 모델이 두 개뿐이므로 T 러너라고 불림

u0(x)=E[Y∣T=0,X]u_0(x)=E[ Y|T=0, X]
u1(x)=E[Y∣T=1,X]u_1(x)=E[ Y|T=1, X]

이러한 모델을 만들면 각 처치에 대한 반사실 예측을 하고 다음가 같이 CATE를 추정할 수 있다.

τ^(x)i=u^(Xi)−u0^(Xi)\hat{\tau}(x)_i=\hat{u}(X_i)-\hat{u_0}(X_i)

  • τ^(x)\hat{\tau}(x) 는 특성 𝑋=𝑥𝑋=𝑥 를 가진 고객의 조건부 평균 처치 효과(CATE)
  • u^(Xi)\hat{u}(X_i)는 마케팅 이메일을 받은 경우의 예상 구매량
  • u0^(Xi)\hat{u_0}(X_i) 는 마케팅 이메일을 받지 않은 경우의 예상 구매량

T러너 다이어그램

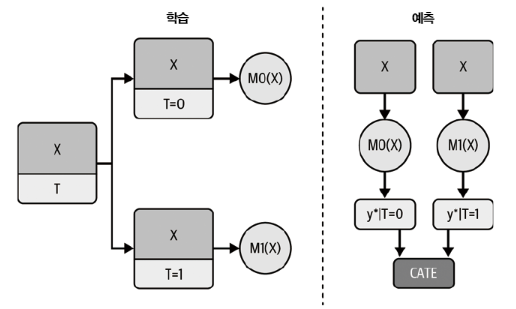
  • 러너가 각자 T = 1 그리고 T = 0에서 머신러닝 모델을 학습. 예측 시점에 두 모델을 모두 사용해서 실험군과 대조군의 차이를 추정함

결과 모델로 boosted regression tree 사용해서 구현
회귀 모델인 LGBMRegressor를 적용

from lightgbm import LGBMRegressor np.random.seed(123)
m0 = LGBMRegressor()
m1 = LGBMRegressor()
m0.fit(train.query(f"{T}==0")[X], train.query(f"{T}==0")[y])
m1.fit(train.query(f"{T}==1")[X], train.query(f"{T}==1")[y]);

두 개의 모델이 있으므로 test set 에서 CATE 예츠갛기 매우 쉬움

t_learner_cate_test = test.assign( cate=m1.predict(test[X]) - m0.predict(test[X])

이 평가 방법은 처치효과가 가장 높은 고객부터 가장 낮은 고객까지 올바르게 정렬했는지에만 관심

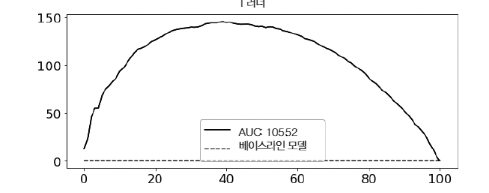
T 러너는 이 데이터셋에서 잘 작동

  • T 러너는 단순한 모델이므로 처치가 이산형으로 주어진 상황일 때 처음 시도하기 좋음
  • 상황에 따라 정규화 편향이 발생하기 쉬움

대조군은 많고 실험군의 데이터는 매우 적은 상황을 생각 -> 이는 처치에 큰 비용이 들어가는 적용 사례에서 매우 흔한 상황
결과 Y에 약간의 비선형성이 있지만, 처치효과는 일정하다고 가정

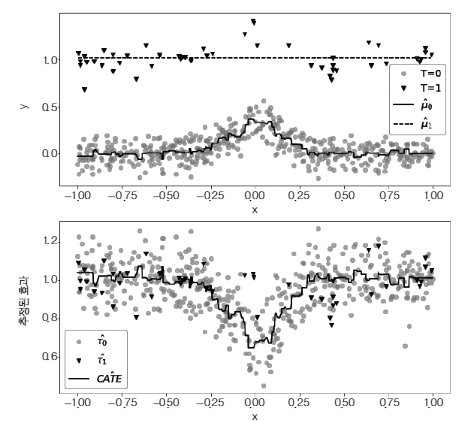
  • 데이터에서 처치를 받은 관측값이 적고 처치를 받지 않은 관측값이 많은 경우, 과적합을 피하기 위해 모델이 과적합되지 않도록 주의
  • 처치를 받은 그룹의 모델 u1^\hat{u_1} 모델은 단순해질 가능성이 크고, 처치를 받지 않은 그룹의 모델 u0^\hat{u_0} 모델은 더 복잡할 수 있지만, 데이터가 풍부하므로 과적합 방지
  • 동일한 하이퍼파라미터를 사용하더라도, 각 그룹의 데이터 크기에 따라 모델의 복잡도와 정규화 정도가 달라짐
  • LightGBM Regressor 모델을 사용하여 min_child_samples=25로 설정했을 때, 데이터가 적으면 트리가 더 작아지고 단순해지는 경향이 있습니다. 이는 모델의 자기 정규화(self-regularization) 효과로 설명할 수 있다.
  • 실제 예시에서 u1^\hat{u_1} 모델은 선형성을 띠고 u0^\hat{u_0} 모델은 비선형성을 포착할 수 있다. 이는 두 모델 간의 차이로 인해 비선형 CATE가 계산될 수 있다.
  • 그러나 실제 CATE는 일정하게 1이므로, 이는 잘못된 결과를 초래할 수 있다.

X-러너(X-learner)는 이러한 문제를 해결하는 방법으로 등장. X-러너는 각 그룹의 데이터를 더욱 효과적으로 활용하여 처치 효과를 추정할 수 있도록 도와줌

X 러너

  • X-러너는 데이터 크기에 따른 모델의 차이와 비선형성 문제를 해결하기 위해 고안된 방법.
  • 처치를 받은 그룹과 처치를 받지 않은 그룹의 모델을 각각 학습한 후, 이들을 결합하여 보다 정확한 CATE를 추정.
  • 이를 통해 데이터가 적은 그룹에서도 비선형성을 잘 포착할 수 있다.

더 복잡하지만 보다 정확한 처치 효과를 추정

단계 1: T-러너와 동일한 과정:

  • 먼저, 고객을 두 그룹으로 나눔: 이메일을 받은 그룹과 받지 않은 그룹.
  • 각 그룹에 대해 모델을 적합시킴:
    • u1^\hat{u_1}: 이메일을 받은 그룹의 구매 예측
    • u2^\hat{u_2}: 이메일을 받지 않은 그룹의 구매 예측

단계 2: 누락된 잠재적 결과 추정:

  • 각 그룹의 모델을 사용해 누락된 결과를 예측:
    • 이메일을 받지 않은 그룹의 데이터로 이메일을 받은 경우의 결과를 예측
    • 이메일을 받은 그룹의 데이터로 이메일을 받지 않은 경우의 결과를 예측

단계 3: CATE 계산:

각각의 그룹에서 CATE를 계산:

  • τ1^(x)=u1^(X)−u0^(X)\hat{\tau_1}(x)=\hat{u_1}(X)-\hat{u_0}(X)
  • τ0^(x)=u1^(X)−u0^(X)\hat{\tau_0}(x)=\hat{u_1}(X)-\hat{u_0}(X)

단계 4: 두 모델 결합:

  • 두 모델을 결합할 때, 더 정확한 모델에 더 많은 가중치를 부여. 이는 성향점수(propensity score)를 사용해 가중치를 설정:
    • τ1^(X)=e(X)τ1^(X)−(1−e(X))τ0^(X)\hat{\tau_1}(X)=e(X)\hat{\tau_1}(X)-(1-e(X))\hat{\tau_0}(X)
    • 여기서 e(X)는 성향점수로, 특정 고객이 이메일을 받을 확률을 나타냄.

왜 X-러너가 더 나은가 ?

  • 정확한 가중치 부여: X-러너는 더 정확한 모델에 더 많은 가중치를 부여하여 잘못된 결과를 최소화합니다.
  • 데이터 활용: 이메일을 받지 않은 그룹의 많은 데이터를 잘 활용하면서, 적은 데이터를 가진 이메일 받은 그룹의 모델도 적절히 활용합니다.
  • 비선형성 보정: 데이터 불균형으로 인한 비선형성을 보정하여 더 정확한 CATE를 추정

연속형 처치 메타러너

  • 레스토랑 체인은 데이터를 분석하여 고객의 할인 민감도를 파악하고, 이를 바탕으로 최적의 할인 시기를 결정할 수 있다.
  • CATE를 정확히 추정하면, 고객 반응을 극대화할 수 있는 할인 정책을 설계할 수 있다.
rest_iddaymonthweekday...is_novcompetitors_pricediscountssales
002016-01-0114...False2.88079.0
102016-01-0215...False2.64057.0
202016-01-0316...False2.085294.0
302016-01-0410...False3.3715676.5
402016-01-0511...False3.79066.0
  • 할인이 처치이고 매출이 결과
  • 일련의 날짜 관련 특성들(월, 요일, 휴일 여부 등)도 포함
  • 목표는 CATE 예측이므로 데이터셋을 학습 및 테스트 데이터셋으로 분할하는 것이 가장 좋음
  • 이 경우, 시간 차원을 활용하여 이러한 데이터셋을 구성 할 수 있음

tain = data_cont.query("day<'2018-01-01'")
test = data_cont.query("day>='2018-01-01'")

가장 먼저 S 러너 시도

S 러너

  • 가장 기본적인 방식
  • 단일 머신러닝 모델 u1^\hat{u_1} 를 사용하여 추정

S 러너의 기본 개념

  • 단일 모델 사용: S 러너는 단일 머신러닝 모델을 사용하여 처치 변수와 결과 변수를 함께 학습
  • 모델 적합: 처치 변수(T)와 다른 모든 특징(X)을 사용하여 결과(Y)를 예측
  • CATE 계산: 모델의 예측값을 이용해 조건부 평균 처치 효과를 추정

수식

us^(x,t)=E[Y∣X=x,T=t\hat{u_s}(x,t) = E[Y|X =x ,T=t]
1.모델 학습:

  • 단일 모델 us^\hat{u_s}를 학습시켜 𝑌를 X와 𝑇에 대해 예측.
  • 예를 들어, us^(x,1)\hat{u_s}(x,1)은 특정 고객이 할인을 받았을 때의 예측 매출, us^(x,0)\hat{u_s}(x,0)은 할인을 받지 않았을 때의 예측 매출을 의미.

2.CATE 계산:

  • 특정 고객의 CATE는 다음과 같이 계산:
    • τ^(x)=us^(x,1)−us^(x,0)\hat{\tau}(x) = \hat{u_s}(x,1)-\hat{u_s}(x,0)

EX

CATE를 추정하려면 결과 Y를 예측하려는 모델에 처치변수를 특성으로 포함하면 됨

X = ["month", "weekday", "is_holiday", "competitors_price"]
T = "discounts"
y = "sales"
np.random.seed(123)
s_learner = LGBMRegressor()
s_learner.fit(train[X+[T]], train[y]);

  • 이 모델은 처치효과를 직접 출력하지 않고, 오히려 반사실 예측값을 구함
  • 즉 다양한 처치에서의 예측 가능
  • 처치가 이산형인 경우에도 이 모델은 여전히 작동할 것
  • 실험군과 대조군의 예측값 차이가 CATE 추정값이 됨

연속형 처치는 약간의 추가작업이 필요

  • 처치의 그리드를 정의
  • 예시에서는 할인율이 0부터 40%까지 변하므로 [ 0,10,20,30,40 ] 그리드 사용 가능
  • 예측하고자 하는 데이터를 확장하여 각 행이 그리드의 각 처칫값을 한번씩 복사해야 함
  • 이를 수행하는 가장 쉬운 방법은 그리드의 값이 있는 데이터 프레임을 예측하려는 데이터에 교차조인 하는 것

    t_grid = pd.DataFrame(dict(key=1, discounts=np.array([0, 10, 20, 30, 40])))
    test_cf = (test .drop(columns=["discounts"]) .assign(key=1) .merge(t_grid) # 확장된 데이터에서 예측하기 .assign(sales_hat = lambda d: s_learner.predict(d[X+[T]])))
    test_cf.head(8)

rest_iddaymonthweekday...saleskeydiscountssales_hat
002018-01-0110...251.51067.957972
102018-01-0110...251.5110444.245941
202018-01-0110...251.5120793.045769
302018-01-0110...251.51301279.640793
402018-01-0110...251.51401512.630767
502018-01-0211...541.01065.672080
602018-01-0211...541.0110495.669220
702018-01-0211...541.01201015.401471

앞 단계에서 각 실험 대상(이 경우 날짜 ) 에 대해 처치 반응 함수 Y(t)의 대략적인 버전을 추정했음
몇몇 실험 대상(일) 에 대한 곡선을 그려서 어떤 모습인지 확인해보겠음
다음 그래프에서 크리스마스인 2018년 12월 25일에 추정된 반응 함수가 2018년 6월 18일보다 더 가파른 모습을 볼 수 있다. 이는 고객이 6월의 특정 날보다 크리스마스에 할인에 더 민감함을 모델이 학습했음을 의미

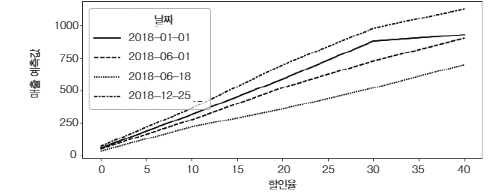
각 날짜와 할인율에 대한 반사실 예측을 수행했지만 CATE 예측을 하지 않아 배운 평가방법을 사용할 수 없음

  • 실험 대상 수준의 곡선을 단일 숫자로 요약하여 처치효과를 나타내는 CATE 추정값을 얻어야 함.
  • 방법: 선형회귀를 사용하여 각 실험 대상에 대해 회귀분석을 수행하고, 처치의 기울기 매개변수를 추출하여 CATE 추정값으로 활용.

단순선형회귀 계수를 사용하여 기울기 매개변수를 추출

β^=Cov(t,y)/Var(t)\hat{\beta}=Cov(t,y)/Var(t)

1.기울기 매개변수 요약 함수 정의:

  • 각 실험 대상의 곡선을 기울기 매개변수로 요약하는 함수를 정의.

2. 데이터 그룹화 및 함수 적용:

  • 확장된 테스트 데이터를 rest_id와 day별로 그룹화하고, 각 그룹에 기울기 함수를 적용.
  • 결과는 인덱스가 rest_id와 day인 판다스 시리즈가 되며, 이 시리즈의 이름을 cate로 지정.

3. CATE 예측값 조인:

  • 생성된 시리즈를 원래 테스트 셋에 조인하여 각 날짜 및 레스토랑의 CATE 예측값을 얻음.

from toolz import curry
@curry
def linear_effect(df, y, t): return np.cov(df[y], df[t])[0, 1]/df[t].var()
cate = (test_cf .groupby(["rest_id", "day"]) .apply(linear_effect(t="discounts", y="sales_hat")) .rename("cate")) test_s_learner_pred = test.set_index(["rest_id", "day"]).join(cate)
test_s_learner_pred.head()

이제 CATE 예측값이 있으므로 모델을 평가 할 수 있음


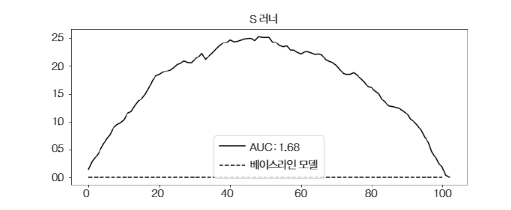
누적 이득 곡선에서 볼 수 있듯이 S 러너는 간단하지만 이 데이터셋에서 괜찮은 성능을 보임

  • 랜덤화된 데이터가 많고 상대적으로 쉬운 해당 데이터셋에 특화된 성능
  • 실제로 S 러너는 그 단순함 때문에 어떤 인과 문제에도 처음 시도하기 좋은 선택
  • 첫째, S 러너는 랜덤화된 데이터가 없어도 괜찮은 성능을 보이는 경향
  • 둘째, S 러너는 이진 및 연속형 처치 모두 활용

S 러너의 단점과 해결책 요약

문제점: S 러너의 편향

  • 정규화 문제: S 러너는 일반적으로 정규화된 머신러닝 모델을 사용하기 때문에, 추정된 처치효과(ATE)가 0으로 편향되는 경향.
  • 실제 사례: 빅터 체르노주코프 등이 작성한 논문에서 시뮬레이션 데이터를 사용하여 S 러너의 ATE 추정을 분석한 결과, 추정된 ATE가 실제 ATE보다 왼쪽으로 편향되어 0에 가까운 경향을 보임.
  • 추정된 ATE의 분포: 시뮬레이션과 추정을 500회 반복한 결과, 추정된 ATE가 실제 ATE보다 작게 나타나는 경우가 많음.
  • 처치변수의 영향력: 처치변수가 다른 공변량보다 결과를 설명하는 데 영향력이 작을 경우, S 러너는 처치변수를 완전히 무시할 수 있다. 이는 선택한 머신러닝 모델과 정규화 정도에 따라 문제가 더 심해질 수 있다.

해결책: 이중/편향 제거 머신러닝 (R 러너)

  • R 러너 소개: 체르노주코프 등이 제안한 방법으로, S 러너의 편향 문제를 해결하기 위해 고안된 방법
  • 방법: 이중/편향 제거 머신러닝을 통해 처치효과 추정에서 발생하는 편향을 줄이고, 보다 정확한 ATE 추정을 가능하게 함.

    이중/편향 제거 머신러닝 (Double/Debiased Machine Learning)

    개념

  • 이중/편향 제거 머신러닝(또는 R 러너)은 FWL 정리의 정제된 버전
  • 결과와 처치의 잔차를 구성할 때 머신러닝 모델을 사용하는 간단하면서도 강력한 방법.
  • 이 접근법은 복잡한 상호작용과 비선형성을 잘 포착하며, 다음과 같은 단계로 이루어짐:

1. 결과 Y 추정

  • 머신 러닝 회귀 모델 uyu_y를 사용하여 특성 X로 결과 Y를 추정
  • uy^(X)=E[Y∣X]\hat{u_y}(X)=E[Y|X]

2. 처치 T 추정

  • 머신 러닝 회귀 모델 utu_t를 사용하여 특성 X로 처치 T를 추정
  • ut^(X)=E[T∣X]\hat{u_t}(X)=E[T|X]

3. 잔차 계산

  • 결과의 잔차 : Y~=Y−μ^y(X)\tilde{Y} = Y - \hat{\mu}_y(X)
  • 처치의 잔차 : T~=Y−μ^t(X)\tilde{T} = Y - \hat{\mu}_t(X)

4. 잔차 회귀 :

  • 결과의 잔차를 처치 잔차에 대해 회귀하여 인과 매개변수(ATE)를 추정

    Y~=τT~+α\tilde{Y} = \tau \tilde{T} + \alpha

  • 여기서 (τ)(\tau)는 OLS를 사용하여 추정된 인과 매개변수입니다.

이중/편향 제거 머신러닝(R 러너)은 복잡한 상호작용과 비선형성을 잘 포착하여 정확한 인과 추정을 가능하게 한다. R 러너는 잔차를 사용하여 처치 효과를 추정하는 방법이다.
하지만

  • 동일한 데이터에서 모델을 적합하고 잔차를 구하면 과적합이 발생할 수 있다.
  • 교차 예측(cross prediction)과 아웃 오브 폴드(out-of-fold) 잔차를 사용. 데이터를 K개의 폴드로 분할하고, K-1개의 폴드에서 모델을 학습한 후 남겨진 폴드에서 잔차를 계산

이중 머신러닝으로 CATE 추정

CATE 추정

τ^(X)=Cov(T,Y)Var(T)\hat{\tau}(X) = \frac{\text{Cov}(T, Y)}{\text{Var}(T)}

손실 함수

R 러너는 다음의 손실 함수를 최소화합니다.

L(τ)=1n∑i=1n(Y~i−τT~i)2L(\tau) = \frac{1}{n} \sum_{i=1}^{n} \left( \tilde{Y}_i - \tau \tilde{T}_i \right)^2
profile
이상억
이상억
이전 포스트

인과추론-그래프 인과모델

0개의 댓글