Binary lifting

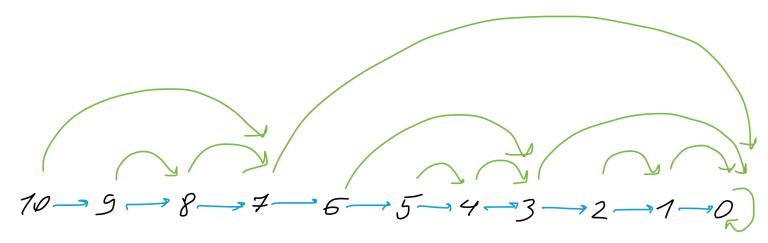
What is Binary lifting?

Binary lifting이란 Binary Search와 Divded & Conquer와 비슷하게 O(logN)에 특정 값을 찾는 것이다. 주로 트리에서 사용된다.

예를들어 현재 노드 V에서 K번째 조상 노드를 찾고 싶다하면 그냥 연산을 통하면 O(n)의 연산, 정확하게 말하자면 트리의 깊이만큼 연산이 이루어진다. 하지만 Binary lifting을 사용하면 값을 찾는데에 O(logN) 만큼의 시간이 걸린다.

How to use it?

이름에서 알 수 있듯이 2의 제곱만큼의 조상 노드를 미리 다 구해놓는 것이다. 따라서 K = 19 라는 값이 주어진다면 16개의 노드를 한번에 점프하고 2개의 노드를 점프하고 1번 점프함으로써 바로 조상의 노드를 찾을 수 있다. 그렇다면 우선 조상 노드들의 배열을 미리 구해놓아야 한다.

int parent[n] // 각 노드의 부모노드가 저장되 있는 배열
vector<vector<int>> up // 2^n번째 노드를 저장할 벡터

LOG = 0;
while((1 << LOG) <= N){
	LOG++; // 해당 트리의 최대 2^log 의 값을 구한다.
}

up = vector<vector <int>>(n, vector<int>(LOG));

parent[0] = 0;
//문제의 조건 i < parent[i] 때문에 이런식으로 작성
//보통은 지수를 구하는것이 제일 바깥 for문이 되어야함
for(int V =0; V < n; V++){
	up[V][0] = parent[V];
    	for(int j = 1; j < LOG; j++){
        	up[V][j] = up[ up[V][j - 1] ][j - 1];
           
        }
}

//time complexity = O(N*logN)

up[V][j] = up[ up[V][j - 1] ][j - 1]; 코드에 대해 설명하자면,

• up[v][0]에는 현재 v노드의 부모 노드가 들어간다.
• up[v][1]에는 up[v][0]의 부모노드의 부모노드가 들어간다.
• up[v][2]에는 up[v][1]의 조부모 노드, 즉 현재 V노드의 조부모 노드의 조부모 노드가 들어간다.

말로 풀어쓰면 어려운데, 각각의 up[v][j]에는 현재 v노드의 2^j번째의 조상노드가 들어간다고 생각하면된다.

이렇게 조상노드들을 미리 계산해놓으면 조상노드를 찾는 방법은 매우 쉽다.

int node; // v노드
int k; // k번째 노드

for(int i = 0; i < LOG; j++){
	if( k & (1 << i)){
    		node = up[node][i]
    }
}

return node;

//time complexity = O(logN)

즉 K = 19라면 이진수로 16 + 2 + 1 = 10011로 바꿀수 있고 i를 미리 구해놓은 LOG의 값까지 증가시키면서 켜진 비트를 찾는 과정이다. 켜져있는 비트만큼 점프를 하면 그게 찾고있는 k번째에 존재하는 조상노드이다.

그렇다면 만약 k 가 현재 노드의 깊이보다 긴 값을 요구할 경우에는 어떻게 해야할까? 미리 해당 노드의 깊이를 구해놓고 해당 노드의 깊이보다 큰 값을 요구 할 경우 문제의 조건에 따라 최상위 노드 혹은 원하는 값을 반환하면 된다.

해당 부분까지 수정한 최종 코드는 다음과 같다.

구현

int parent[n] // 각 노드의 부모노드가 저장되 있는 배열
vector<vector<int>> up // 2^n번째 노드를 저장할 벡터
vector<int> depth // 노드의 깊이를 저장

LOG = 0;
while((1 << LOG) <= N){
	LOG++; // 해당 트리의 최대 2^log 의 값을 구한다.
}

up = vector<vector <int>>(n, vector<int>(LOG));
depth = vector<int>(n);

parent[0] = 0;
for(int V =0; V < n; V++){
	up[V][0] = parent[V];
        if(V != 0){
            depth[V] = depth[parent[V]] + 1; //depth
        }
    
    	for(int j = 1; j < LOG; j++){
        	up[V][j] = up[ up[V][j - 1] ][j - 1];
           
        }
}

//time complexity = O(N*logN)

int getKthAncenstor(int node, int K){
	if( depth[node] < K){
    	// 문제 조건에 맞게 수행
    	}

        for(int i = 0; i < LOG; j++){
            if( k & (1 << i)){
                    node = up[node][i]
            }
        }
  
	return node;
    //time complexity = O(logN)
}