이분 매칭(Bipartite Matching)이란?
이분 그래프에서 A 그룹의 정점에서 B 그룹의 정점으로 간선을 연결 할 때,
A그래프의 하나의 정점이 B그래프 하나의 정점만 가지도록 구성된 것이 이분 매칭이다.
이분 그래프(Bipartite Graph)란?
이분 그래프 :: 정점을 두개의 그룹으로 나누었을 때,
존재하는 모든 간선의 양 끝 정점이 서로 다른 그룹에 속하는 형태의 그래프를 의미한다.
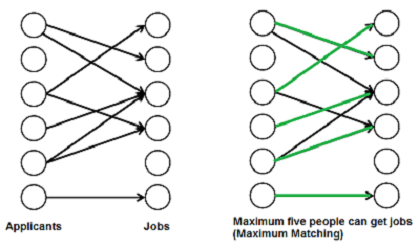
좌측은 이분 그래프이지만 이분 매칭은 아니고 우측은 둘다 맞다.
이분 매칭의 원리
A그룹과 B그룹으로 나누어서 A그룹을 기준으로 설명하겠다.
- DFS로 푼다.
- A 집단의 첫 번째 노드가 연결할 수 있는 B 집단의 노드와 연결한다.
- A 집단의 두 번째 노드가 연결할 수 있는 B 집단의 노드와 연결한다.
만약 현재 A집단의 두번째 노드가 연결하려는 B 집단의 노드가 이미 A집단의 첫 번째 노드와 연결된 상태이면,
1) A 집단의 두 번째 노드가 B 집단의 다른 노드를 찾거나,
2) 연결할 다른 노드가 없는 경우는 첫 번째 노드에게 B 집단의 다른 노드와 연결할 수 있는 지 요청해서 있는 경우, 첫 번째 노드가 다른 노드와 연결하고, 두 번째 노드가 A의 첫 번째 노드와 연결되어 있던 B 집단의 노드와 연결된다.
구현
시간 복잡도: O(n*m)
n, m = 4, 4 # A집단과 B집단의 정점의 개수
adj = [[0 for _ in range(n)] for __ in range(m)]# A집단의 노드와 B집단의 노드가 연결 돼있는가 확인하는 배열
aGroup = [-1 for _ in range(n)] # A그룹의 노드들
bGroup = [-1 for _ in range(m)] # B그룹의 노드들
visit = [0 for _ in range(MAX_N)] # 방문을 체크하는 배열
visitCnt = 0 # visitCnt를 통해 몇번째 노드가 방문중인지 체크한다.
// A의 정점i와 B의 정점 j가 연결되어 있으면 1로 표시
adj[0][0] = 1;
adj[0][1] = 1;
adj[0][3] = 1;
adj[1][0] = 1;
adj[1][1] = 1;
adj[2][0] = 1;
adj[2][2] = 1;
adj[3][2] = 1;
adj[3][3] = 1;
size = 0
for i in range(n):
visitCnt +=1
if dfs(i):
size += 1 #연결된 노드의 개수
#A의 정점인 An에서 B의 매칭되지 않은 정점으로 가는 경로를 찾는다.
def dfs(current):
if visit[current] == visitCnt: # 만약 visitCnt와 값이 같다면 이미 연결된 노드가 방문중임
return False
visit[current] = visitCnt
for next in range(m):
if adj[a][b]: #서로가 연결되있고
if bMatch[b] == -1 or dfs(bMatch[b]) # B노드가 연결이 안되있거나 연결 돼있던 A노드가 다른 갈곳이 있다면
bMatch[b] = a #a와 b를 매치시킨다.
aMatch[a] = b
return True
return False
