본 포스트는 KAIST AI대학원 신진우 교수님의 AI602 강의자료를 참고하였습니다.

Normalization

정규화는 왜 필요한 것일까?

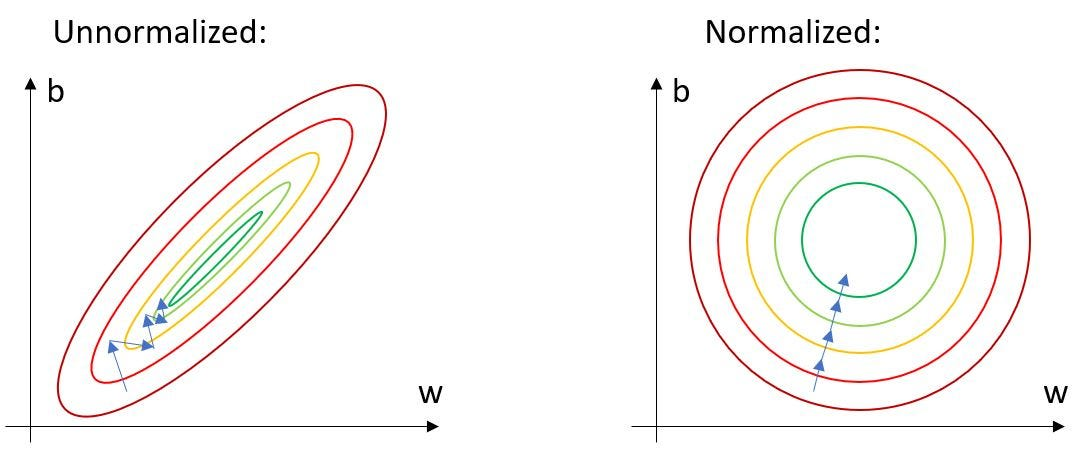
위와 같은 그림에서 unnormalized 상태라면 initial point가 어디냐에 따라 수렴속도도 다를 것이고 높은 learning rate를 사용하기 어려울 것이다.

반면 normalized 데이터에서의 학습은 원형이므로 initial point가 중요하지않고 더 높은 learning rate를 사용하면서 더 작은 error로 수렴할 수 있다.

따라서 입력값에 대해 정규화를 적용하는 것은 optimal parameter를 빠르게 찾기 위한 노력이라고 볼 수 있다.

또한 floating point issue에 대해서도 더 robust하게 대응할 수 있다.

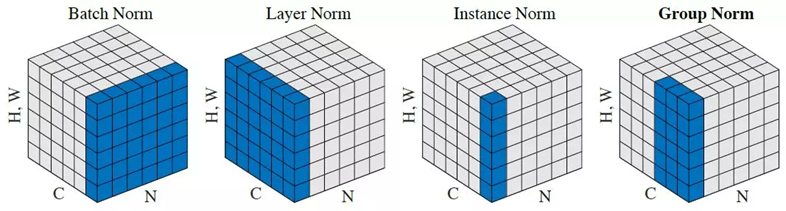
Normalization은 여러가지가 있다.
Batch Norm, Layer Norm, Instance Norm, Group Norm, Weight Norm

이번 포스트에서는 Batch Norm에 대해 다뤄볼 예정이다.

Internal Covariant Shift

Internal Covariant Shift는 네트워크에서 학습이 진행되면서 layer 별로 입력의 데이터 분포가 달라지는 현상을 의미한다.

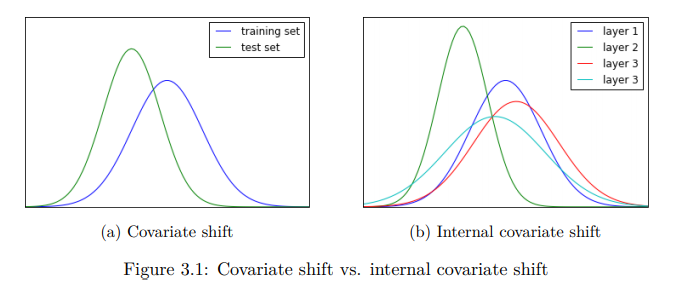
위 figure의 (b)에서 첫번째 layer가 layer 1이고 마지막 layer가 layer 4라고 할 때, 보이는 바와 같이 각 layer의 연산을 마치고 나면 데이터의 분포가 달라질 수 있다. 이 경우 앞선 설명처럼 데이터의 분포가 상이하기 때문에 네트워크의 학습을 위해 높은 learning rate를 사용할 수 없고 가중치 초기값 설정에 영향을 크게 받게 된다.

또한, 한 layer의 output이 다음 layer의 input이 된다는 점을 고려한다면, deep network일수록 네트워크의 각 layer를 지날 때마다 입력 데이터 $x$의 분포에서 점점 멀어질 가능성이 높아진다.

Batch Normalization (배치 정규화)

지금부터의 설명은 Batch Normalization을 최초로 제안한 저자들의 주장을 정리한 것이다.

Batch normalization (BN)은 neural net 안의 internal covariate shift를 줄여 네트워크의 학습을 가속시키는 방법이다. [loffe et al., 2015]

BN은 배치 별 평균과 분산을 구해 정규화 하는 것이다. batch와 layer의 input에 따라 데이터가 서로 다른 분포를 갖고 있더라도 이를 이를 정규화시켜 zero mean gaussian 형태로 만드는 것이다.

zero mean gaussian에서 평균은 0, 분산은 1을 갖게 된다.

무엇에 대한 평균과 분산인가?

우리는 이후 layer normalization을 다룰 것이기 때문에 무엇에 대한 평균과 분산인지 잘 구분해놓아야 한다.

BN에서의 평균과 분산들은 parameters에 대한 batch 속 instance들의 평균과 분산이다.

따라서 Convolution Neural Network (CNN)의 관점에서 parameters는 채널이고, 평균 및 분산은 Batch, Height, Width에 대한 것이 된다.

마찬가지로 Fully Connected Layer (FC)에서는 각 뉴런이 parameters이다.

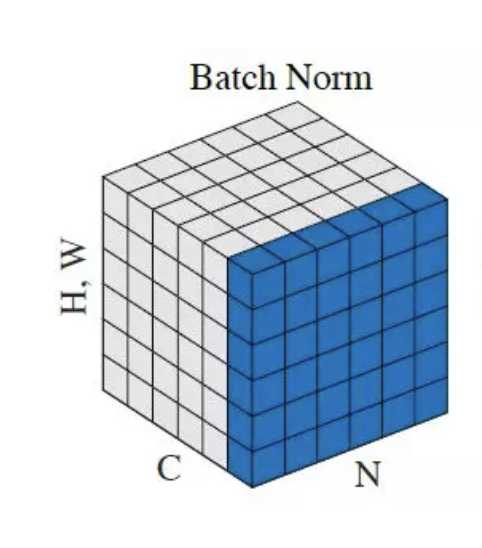
평균과 분산은 다음과 같이 계산된다.

$\mu_{\mathcal{B}} = \frac{1}{m}\sum^{m}_{i=1}x_{i}$

$\sigma^{2}_{\mathcal{B}} = \frac{1}{m}\sum^{m}_{i=1}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2}$

입력값 $x$을 정규화시키면 다음과 같다.

$\hat{x}_{i} = \frac{x_{i} - \mu_{\mathcal{B}}}{\sqrt{\sigma^{2}_{\mathcal{B}}+\epsilon}}$ ($\epsilon$은 divide-by-zero를 방지하기 위한 term이다)

이후 $\hat{x}_{i}$가 affine transform을 거친다.

$y_{i} = \gamma\hat{x}_{i} + \beta = \text{BN}_{\gamma, \beta}\left(x_{i}\right)$ where $\gamma$ and $\beta$ are learnable parameters

이 때, $\gamma$와 $\beta$는 데이터의 분포를 옮길 수 있는 여지를 주는 learnable parameters이다.

앞서 언급한 zero mean gaussian의 분포에서 데이터를 약간 움직일 수 있도록 해주는 것인데, 이러한 유연함이 학습에 더 효과적일 수 있다.

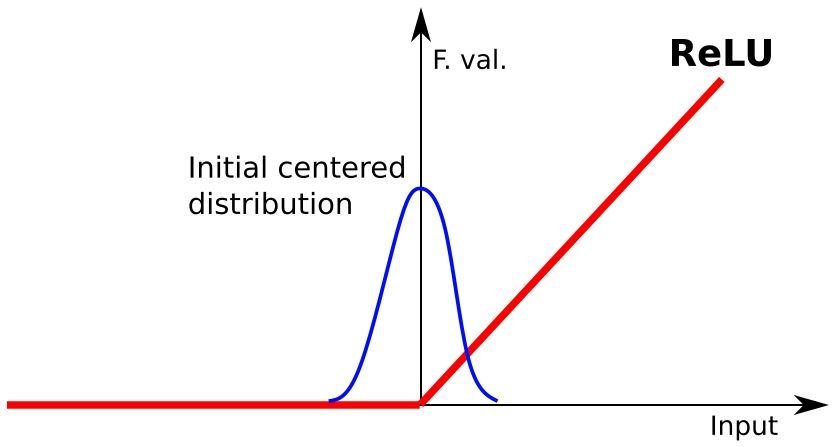
이는 ReLU activation function을 생각해보면 알 수 있다.

zero mean gaussian 분포에서는 절반의 데이터는 0이 되어 이후 layer들의 학습에 활용되지 못하게 된다.

따라서 learnable parameter를 통해 분포를 움직여 주게 됨으로써 gradient vanishing problem도 해소할 수 있다.

결과적으로, BN의 수식을 정리하면 다음과 같다.

$BN(X)=\gamma({X-\mu_{\mathcal{B}} \over \sigma_{\mathcal{B}}})+\beta$

BN in Training Time

BN은 training time과 testing time이 다르게 동작하는데, 그 이유는 testing time에서는 batch 단위로 들어오지 않아 batch 별 평균과 분산을 구하는 것이 어렵기 때문이다.

이미지 10장을 mini-batch로 사용하는 training의 상황과 이미지 1장에 대해 네트워크를 통과시켜야하는 testing 상황을 가정해본다면 쉽게 이해할 수 있다.

Training time에서는 평균과 분산을 batch별로 계산한다.
따라서 평균과 분산도 다음과 같이 계산된다.

다음으로 Training time에서 mini-batch의 분포를 해석해보자.

앞서 살펴본 BN의 식은 다음과 같다.

즉, training time에서 $y$의 분포는 오직 $\gamma$와 $\beta$에만 의존한다. training time의 mini-batch는 항상 0과 1로 normalize되기 때문이다.

BN in Testing Time

Testing time에서의 BN은 batch별 평균과 분산을 구하는 것이 어렵기 때문에 training time에서 구했던 batch 별 평균의 분산을 평균내어 사용한다.

따라서 평균과 분산이 다음과 같이 계산된다.

$\sigma^2$의 식은 표본 분산의 평균 공식에서 자유도(degree of freedom)를 하나 잃어 M-1로 나누는 개념과 동일하다.

당연히, $\mathbb{E}_{\mathcal{B}}[\mu_{\mathcal{B}}]$과 ${m \over m-1}\mathbb{E}_{\mathcal{B}}[\sigma^2_{\mathcal{B}}]$는 testing time input의 $\mu$, $\sigma^2$와 차이가 있을 것이다.

이는 각 mini-batch에 Noise Injection Effect를 부여하는 것으로 Regulariation Effect를 갖는 것과 같다.

Analysis of Batch Normalization

Batch size는 결국 중심 극한 정리(CLT; Central Limit Theorem)의 sample size와 같다. Batch Norm이 잘 작동하는 수학적인 background도 CLT인 셈이다.

CLT에 따르면 모집단이 어떠한 분포를 따르던 sample size가 클수록 정규분포에 가까워진다. 반면, sample size가 너무 작을 경우에는 분포가 skewed되는 등 정규분포를 따르지 않는 문제가 발생한다.

그렇다면 Batch Norm에서도 무조건 큰 sample size가 좋은가?

그렇지 않다. 적절한 batch size를 고르는 것이 좋다.

지나치게 큰 batch size더라도 noise를 감소시켜 모델이 빠르게 수렴할 수 있을 것으로 기대되지만 다음의 두 가지 이유로 좋지 않다.

1. batch size가 매우 크다면 전체 training set의 gradient를 구하는 BGD (Batch Gradient Descent) 방식에 가까운 것인데, DNN에서 mini-batch SGD (Stochastic Gradient Descent)가 BGD보다 local-minima에 더 robust함이 밝혀져있으므로 지나치게 큰 batch size는 좋지 못하다.

2. Computational Problem (GPU의 한계)

반대로 지나치게 작은 batch size는 다음과 같은 이유로 좋지 않다.

1. 중심 극한 정리를 만족하지 못해 평균과 표준 편차가 데이터의 전체 분포를 잘 설명하지 못한다.

2. noise가 커지게 되므로 regularization 효과가 지나치게 커져 성능이 좋지 못할 수 있다.

3. 모델의 수렴이 불안정하다.

따라서 적절한 크기의 batch size를 잡는 것이 중요하다. 적절한 크기의 batch size는 regularization 효과도 가지면서 training speed도 빠르게 할 수 있다.

Facebook의 TASKNORM: Rethinking "Batch" in BatchNorm (2021) 에서도 32~128 사이의 batch size를 선택할 것을 권장하고 있다.

이러한 Batch Normalization의 한계를 극복하기 위해 Layer Norm과 Weight Norm 등이 등장하였다.

Conclusion

1. BN은 더 큰 learning rate를 사용할 수 있게하여 학습을 가속한다.
2. BN은 saturating non-linearities에서의 gradient vanishing을 안정화한다.
3. BN은 regularization effect가 있어 weight decay와 dropout layers를 줄일 수 있다.
4. BN의 batch size는 적당한 크기로 잡는 것이 좋다.
5. 사실 BN은 Internal Covariant Shift를 해결하지 못한다. 따라서 학습 속도 개선도 ICS와 무관하다. 아래 후속 논문에서 자세히 다룰 예정이다.

References

https://arxiv.org/abs/1502.03167
https://towardsdatascience.com/how-to-calculate-the-mean-and-standard-deviation-normalizing-datasets-in-pytorch-704bd7d05f4c
https://medium.com/geekculture/tagged/internal-covariate-shift
https://www.researchgate.net/figure/Schematic-of-the-distribution-of-incoming-information-to-a-ReLU-activation-function-a_fig5_339470869
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2771718/
https://subinium.github.io/introduction-to-normalization/