[논문 요약] Layer Normalization

🎈 Introduction

고성능의 Deep Neural Network(DNN)의 학습에는 계산 비용이 굉장히 크게 든다.

DNN의 훈련 시간을 줄이는 방법에는 뉴런들을 Normalize(정규화)하는 것이 있다.

대표적인 Normalize 기법에는 Batch Normalization이 있는데, 이는 DNN의 훈련 시간을 줄이는 것에 크게 기여했다.

하지만, mini-batch 사이즈에 영향을 받고, RNN에는 어떻게 적용되어야 하는지 명확히 알려지지 않았다.

본 논문에서 소개하는 Layer Normalization을 Batch Normalization과 비교하면 다음과 같다.

공통점

• 각 뉴런마다 adaptive bias와 gain 파라미터를 보유한다

차이점

• Train 모드와 Test 모드에서 똑같이 동작한다
• RNN 의 은닉층들을 안정화시키는 것에 매우 효과적이다.

Feed Forward Network는 각 layer마다 Normalization에 이용되는 통계를 저장하고 계속해서 사용할 수 있지만, Recurrent Neural Network는 인풋의 길이가 달라지기 때문에 Time-step에 따라서 다른 통계를 써야 한다.

이와 같은 네트워크의 차이 때문에 Batch Normalizatoin은 사용할 수 없지만, Layer Normalization은 각 layer에서 곧바로 은닉층 인풋의 정규화 통계를 계산할 수 있기 때문에 RNN에 적용시킬 수 있다.

🎨 BackGround

Deep Learning의 문제점
특정 layer 가중치의 gradient가 이전 layer 출력값들에 크게 영향을 받는다.

Batch Normalization은 배치의 모든 샘플에 대해서 은닉층의 각 뉴런으로 들어오는 인풋들의 총합을 정규화하여 이 문제를 해결한다.

$\overline{a}^l_i=\frac{g^l_i}{\sigma^l_i}(a^l_i-\mu^l_i)$

$\mu^l_i= \underset{\textbf{x}\sim \textbf{P(x)}}{\mathop{\mathbb{E}}}\,[a^l_i]$

$\sigma^l_i=\sqrt{\underset {\textbf{x}\sim\textbf{P(x)}}{\mathop{\mathbb{E}}}[(a^l_i-\mu^l_i)^2]}$

$\overline{a}^l_i$ : $l^{th}$ layer의 $i^{th}$ hidden unit으로 들어가는 인풋 총합의 정규화값
$g_i$ : 비선형 활성화 함수 이전에 정규화 활성화의 크기를 결정하는 값
$\mu$, $\sigma$ : mini-batch의 샘플들을 이용해 추정된다.

🍳Layer normalization

연구진은 Batch Normalization의 단점을 극복하기 위해 Layer Normalization을 구상하게 되었다.

Covariate Shift
특정 layer output의 변화가 다음 layer로의 인풋 총합에 correlated 변화를 크게 일으킨다.

이러한 covariate shift 문제는, 각 layer에서의 인풋 총합의 mean과 variance를 고정시킴으로써 해결할 수 있다.

연구진은 다음과 같은 공식에 의해 특정 layer의 모든 은닉층 뉴런에 대해 정규화 통계를 계산한다.

$\mu^l={1\over H}{\underset{i=1}{\overset{H}{\sum}}}a^l_i$

$\sigma^l = \sqrt{{1\over H}{\underset{i=1}{\overset{H}{\sum}}}{(a^l_i-\mu^l)^2}}$

Batch Normalization 수식과의 차이점

• Layer Normalization에서는 같은 layer에 있는 모든 은닉층 유닛들이 정규화 통계량($\mu$, $\sigma$)를 공유한다
• 하지만 배치의 각 훈련 샘플은 서로 다른 정규화 통계량을 갖는다
• mini-batch의 크기에 영향을 받지 않기 때문에 batch size 1의 온라인 학습에도 이용될 수 있다

Layer normalized recurrent neural networks

NLP 문제에서는 훈련 샘플마다 문장의 길이가 달라지는 것이 일반적이다.

RNN은 모든 time-step에서 같은 weight를 사용하기 때문에 이러한 문제를 푸는 것에 효과적이다.

하지만 만약 RNN에 Batch Normalization을 적용한다면 매 time-step마다 다른 통계량을 계산하고 저장해야 할 것이다.

이러한 방식은 test 문장의 길이가 train 문장들보다 길 때 통계량을 이용할 수 없다는 문제를 발생시킨다.

반면 Layer Normalizaion은 현재 time-step에서 특정 layer로 들어오는 인풋 총합의 통계량에 기반하기 때문에 위와 같은 문제가 생기지 않는다.

또한 이 방식은 모든 time-step에 대해서 한 쌍의 gain, bias 파라미터만 공유한다.

$\textbf{h}^t=f[{\textbf{g}\over{\sigma^t}}\odot (\textbf{a}^t-\mu^t)+\textbf{b}]$

$\mu^t={1\over H}{\underset{i=1}{\overset{H}{\sum}}}a^t_i$

$\sigma^t = \sqrt{{1\over H}{\underset{i=1}{\overset{H}{\sum}}}{(a^t_i-\mu^t)^2}}$

표준 RNN에서 위와 같은 수식에 의해 정규화가 진행된다.

🧶Related work

Batch Normalization on RNN

이전에 RNN에 Batch Normalization을 적용하려는 시도가 있었다.
(Batch Normalized Recurrent Neural Networks)

해당 연구진은 각 time-step마다 독립적인 normalization 통계량을 사용하였고, gain 파라미터를 0.1로 초기화했다.

Weight Normalization

Weight Normalization에서는 variance 대신에 앞단 weight들의 L2 norm이 뉴런 인풋 총합을 정규화하는 것에 이용된다.

위의 두 방식은 기존의 feed-forward network에 다른 parameterization을 적용한 것과 같다고 볼 수 있다.

하지만 Layer Normalization은 이러한 re-parameterization이 아니며, 특별한 invariance 성질을 갖는다는 점에서 다르다.

🔍 Analysis

Invariance under weights and data transformations

Layer Normalization이 Batch Normalization, Weight Normalization과 다르다고 하더라도, 이들은 다음과 같은 공통점을 갖는다.

정규화 기법들의 공통점

• 뉴런의 인풋을 두 스칼라값($\mu$, $\sigma$)로 정규화한다
  $h_i = f({g_i \over \sigma_i}(a_i-\mu_i)+b_i)$
• 각 뉴런에서 정규화 이후에 adaptive bias $b$와 gain $g$를 학습한다.

⚽ Weight re-scaling and re-centering

Batch Normalization & Weigth Normalization

단일 뉴런에서 앞단의 가중치 $w_i$의 re-scaling은 정규화된 인풋에 영향을 주지 않는다
weight vector가 $\delta$만큼 scale되면 두 스칼라값 $\mu$, $\sigma$의 값도 $\delta$만큼 scale된다.

따라서, 해당 정규화 기법들은 가중치의 re-scaling에 invariant하다.

Layer Normalization

단일 뉴런 weight vector의 re-scaling에 invariant하지 않다.
대신에 전체 weight matrix의 re-scaling과 shift에 invarant하다.

아래는 이를 증명하는 공식이다.

$\textbf{h}'=f({\textbf{g}\over \sigma'}(W'\textbf{x}-\mu')+\textbf{b})=f({\textbf{g}\over \sigma'}((\delta W'+\textbf{1}\mathbf{\gamma^\top})\textbf{x}-\mu')+\textbf{b})$
$\,\,\,\,\,\,\,=f({\textbf{g}\over \sigma}(W\textbf{x}-\mu)+\textbf{b})=\textbf{h}$

$W$ : 기존 weight matrix
$W'=\delta W'+\textbf{1}\mathbf{\gamma^\top}$  : $\delta$만큼 scale, $\gamma$만큼 shift된 weight matrix

⚾ Data re-scaling and re-centering

모든 정규화 기법이 데이터셋의 re-scaling에 invariant하다.
나아가 Layer Normalization은 개별 훈련 샘플의 re-scaling에도 invariant하다.

$h'_i=f({g_i\over \sigma'}(w_i^\top \textbf{x}'-\mu')+b_i)=f({g_i\over \delta\sigma}(\delta w_i^\top \textbf{x}-\delta\mu)+b_i)=h_i$

$\textbf{x}$ : 기존 훈련 샘플
$\textbf{x}'=\delta\textbf{x}$ : $\delta$만큼 re-scaling된 훈련 샘플

Geometry of parameter space during learning

이론상으로는 위와 같이 안정하더라도, 실제 훈련에서는 예상과 매우 다른 현상이 나올 수 있다.

따라서 이번에는 기하학적인 분석을 통해 정규화가 암묵적으로 학습률을 줄이고 학습을 안정화시킨다는 것을 보일 것이다.

Riemannian metric

확률 모델의 학습 가능한 파라미터들은 '가능한 모든 입출력 관계를 지닌' 부드러운 manifold를 만든다.

확률 모델의 manifold 두 점 사이의 거리를 측정할때는 Kullback-Leibler divergence를 이용하는데, 이때의 parameter space를 Riemannian manifold라고 한다.

Riemannian manifold의 곡률은 Riemannian metric에 의해 $ds^2$으로 표현된다.

이는 parameter space 상의 한 점에서의 접선 방향으로 모델 출력값 변화를 측정한다.

$ds^2=\text{D}_{\text{KL}}[P(y|\textbf{x};\theta)||P(y|\textbf{x};\theta+\delta)]\approx {1\over2}\delta^\top F(\theta)\delta$

$F(\theta)=\underset{\textbf{x}\sim P(\textbf{x}), y\sim P(y|\textbf{x})}{\mathop{\mathbb{E}}}[{\partial \,log\,P(y|\textbf{x};\theta)\over {\partial \theta}}{\partial \,log\,P(y|\textbf{x};\theta)^\top\over {\partial \theta}}]$

$w_i$ 방향의 ${F}_{ij}$는 gain 파라미터 $g$와 정규화 스칼라값 $\sigma_i$에 의해서 조정된다.
$w_i$의 크기가 2배가 되면, 모델의 출력값은 변하지 않더라도 $\sigma_i$가 2배 되어 $w_i$ 방향의 ${F}_{ij}$ 성분이 $1\over 2$배된다.

즉, $w_i$ 방향의 곡률이 $1\over 2$배됨으로써 학습률이 줄어드는 효과가 나와 학습이 안정화된다.

🧪 Experimental results

연구진은 Recurrent Neural Network에 집중하여 다음 6개의 task에 대해서 실험을 진행했다.

• Image-sentence ranking
• question-answering
• contextual language modelling
• generative modelling
• handwriting sequence generation
• MNIST classification

Order embeddings of images and language

이미지와 문장의 joint embedding space를 학습하는 order-embedding 모델을 이용한 실험이다.

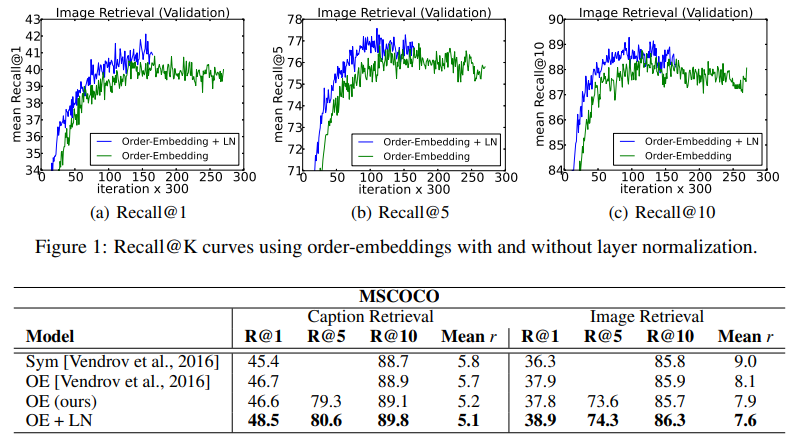
Recall@K : 상위 K개의 예측값 중에서 정답이 있는지 측정하는 지표

모든 실험 케이스에서 Layer Normalizaion 적용 모델이 가장 좋은 성능을 보여주었다.

Teaching machines to read and comprehend

이번 실험은 Layer Normalization과 Batch Normalization을 비교하기 위한 실험이다.

실험 내용은 question-answering task로, 질문이 주어지면 빈칸을 채우는 방식으로 답변해야 한다.

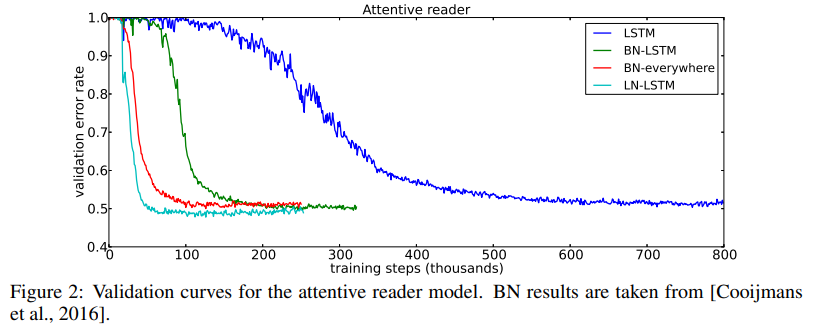
Layer Normalization이 더 빠른 훈련 속도를 보여주었으며 최종 validation 결과도 더 좋았다.

Skip-thought vectors

인접하는 단어가 주어지면 문장은 encoder RNN에 의해 인코딩되고 decoder RNN이 주변 문장들을 예측하는데 이용된다.

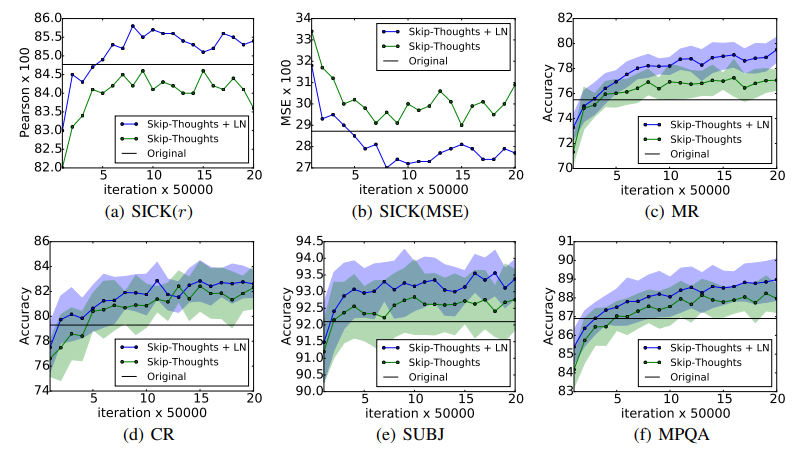Layer Normalization을 적용한 모델이 기본 모델보다 더 빠르게 훈련되었으며 더 좋은 결과를 보여주었다.

Modeling binarized MNIST using DRAW

연구진은 MNIST 데이터셋을 이용해 generative modeling에서도 실험을 진행했다.

Deep Recurrent Attention Writer(DRAW)는 MNIST 숫자들의 분포를 모델링하는 SOTA 모델이다.

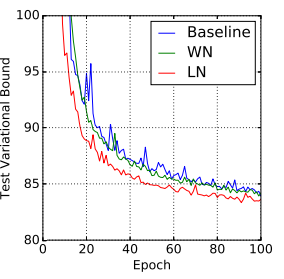
Layer Normalization을 적용한 DRAW가 기본 모델보다 두배 빠르게 수렴했으며 더 좋은 결과를 보여주었다.

Handwriting sequence generation

이전 실험들에서는 대부분 10~40 단어 길이의 NLP task들에 대해서 진행했다.

연구진은 더욱 긴 문장에 대해서도 실험해보기 위해 IAM Online Handwriting Database를 이용한 handwriting generation task를 시행하기로 했다.

IAM-OnDB는 사용자 221명의 손글씨 문장들로 이루어져 있다.

실험 내용은 인풋으로 손글씨 단어들이 들어오면 손글씨 펜 좌표의 시퀀스를 예측하는 것이다.

작은 사이즈의 mini-batch와 굉장히 긴 문장을 사용하기 때문에 안정적인 모델을 구축하는 것이 중요하다.

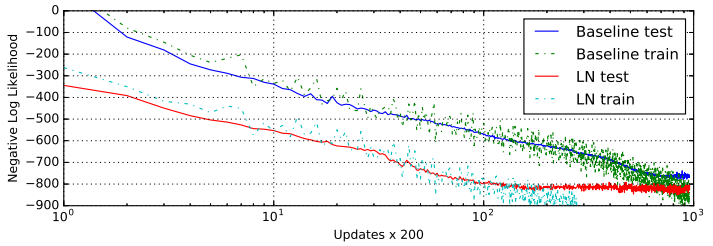
Layer Normalization이 적용된 모델은 기본 모델과 비슷한 결과에 도달했지만 속도는 훨씬 빨랐다.

Permutation invariant MNIST

연구진은 RNN 뿐만 아니라 FFN에서도 Layer Normalization을 실험해보았다.

이전의 분석에서 보였듯이 Layer Normalization은 인풋의 re-scaling에 invariant하다.

하지만 logit의 크기에 의해 예측 신뢰도가 결정된느 logit 출력값들에서는 이러한 성질이 필요하지 않다.

이에 연구진은 마지막 softmax 층을 제외한 FC 층들에 layer normalization을 적용했다.

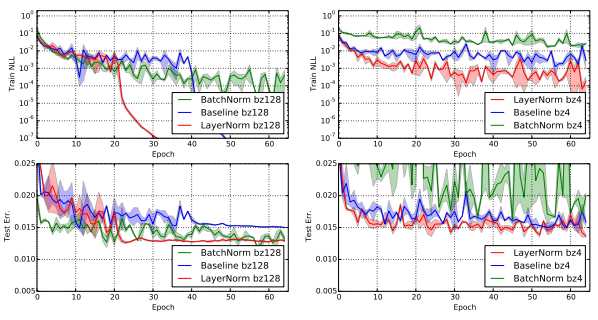연구 결과, Layer Normalization은 batch-size에 민감하지 않고 Batch normalization보다 모델이 더 빠르게 수렴하도록 했다.

Convolutional Networks

연구진은 Convolutional Neural Network에도 Layer Normalization을 적용하는 실험을 진행했다.

Fully Connected layer에서는 모든 은닉층 뉴런들이 최종 결과에 비슷한 기여를 하는데 반해,

Convolutional Neural Network에서는 receptive field가 이미지 모서리 부분에 위치하는 은닉층 뉴런들이 다른 뉴런들에 비해 최종 결과에 거의 기여하지 않는다.

따라서 같은 layer에서도 나머지 뉴런들과 굉장히 다른 정규화 통계량을 갖게 된다.

이에 연구진은 ConvNet에서도 layer normalization을 효과적으로 적용할 수 있는 후속 연구의 필요성을 언급했다.

🎯 Conclusion

• Neural Network의 훈련 속도를 가속시킬 수 있는 Layer Normalization을 소개하였다
• 다른 정규화 기법들과 invariance 성질을 이론적으로 분석하였다
• Layer Normalization은 단일 훈련 샘플의 shifting, scaling에 invariant함을 보였다
• 긴 문장과 작은 사이즈의 mini-batch가 주어졌을 때 RNN이 layer normalization의 효능을 더 많이 받음을 실험적으로 보였다