1. Introduction
Computer Vision에 Attention을 적용하는 트렌드
모델의 블록을 만들 때 과연 Convolutional layer가 우수한 지 고민하게 되었다
CNN으로 하여금 long-range dependency를 학습하도록 도와주는 것을 넘어서, Attention이 CNN을 완전히 대체할 수 있음이 입증되었다
이러한 추세는 학습된 Attention이 CNN과 유사한 역할을 하는 지 의문을 갖도록 했다
본 논문은 Attention layer가 Convolution처럼 동작할 수 있는 것에 대한 근거를 제시 하며,충분한 개수의 Head를 갖는 MHSA는 적어도 Convolution layer보다 expressive함을 증명 한다.
2. Background
Position Encoding을 사용하지 않을 때
I n p u t X Input\,\,\,\,\, X I n p u t X A t t e n t i o n S c o r e A : = X W q r y W k e y T X T Attention\,\, Score\,\,\,\,\, A\,\,:=\,XW_{qry}W^T_{key}X^T A t t e n t i o n S c o r e A : = X W q r y W k e y T X T
S e l f A t t e n t i o n ( X ) t , : : = s o f t m a x ( A t , : ) X W v a l Self\,Attention(X)_{t,:}\,:=\,softmax(A_{t,:})XW_{val} S e l f A t t e n t i o n ( X ) t , : : = s o f t m a x ( A t , : ) X W v a l
이 경우, 문장을 구성하는 토큰의 순서와 상관없이 Self Attention이 항상 같은 결과를 출력한다.
Position Encoding을 사용할 때
I n p u t X Input\,\,\,\,\, X I n p u t X A t t e n t i o n S c o r e A : = ( X + P ) W q r y W k e y T ( X + P ) T Attention\,\, Score\,\,\,\,\, A\,\,:=\,(X+P)W_{qry}W^T_{key}(X+P)^T A t t e n t i o n S c o r e A : = ( X + P ) W q r y W k e y T ( X + P ) T
S e l f A t t e n t i o n ( X ) t , : : = s o f t m a x ( A t , : ) X W v a l Self\,Attention(X)_{t,:}\,:=\,softmax(A_{t,:})XW_{val} S e l f A t t e n t i o n ( X ) t , : : = s o f t m a x ( A t , : ) X W v a l
Attention Score를 계산할 때 인풋에 포지션 인코딩을 더한 값을 넣으면 위와 같은 문제를 해결할 수 있다.
Multi-head self attention
M H S A ( X ) : = c o n c a t h ∈ [ N h ] [ S e l f − A t t e n t i o n h ( X ) ] W o u t + b o u t MHSA(X) := \underset{h \in [N_h]}{concat}[\,Self-Attention_h(X)\,]W_{out}+b_{out} M H S A ( X ) : = h ∈ [ N h ] co n c a t [ S e l f − A t t e n t i o n h ( X ) ] W o u t + b o u t
여러 개의 head를 갖는 self-attention으로, 각각의 Query, Key, Value의 weight가 다르다 각 head에 따라 계산한 self-attention 결과 행렬을 옆으로 concat하고, W o u t W_{out} W o u t D i n D_{in} D i n D o u t D_{out} D o u t
Convolutional layer
Conv 필터 수식
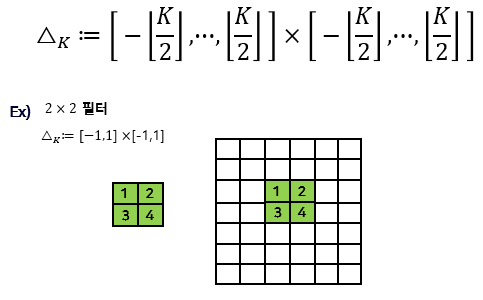
C o n v ( X ) i , j : = ∑ ( δ 1 , δ 2 ) ∈ △ K X i + δ 1 , j + δ 2 , : W δ 1 , δ 2 , : , : + b Conv(X)_{i, j} := \sum_{{(\delta_1, \delta_2)\in \bigtriangleup_K}} X_{i+\delta_1, j+\delta_2, :} W_{\delta_1, \delta_2, :, :} + b C o n v ( X ) i , j : = ∑ ( δ 1 , δ 2 ) ∈ △ K X i + δ 1 , j + δ 2 , : W δ 1 , δ 2 , : , : + b
이미지의 i i i j j j ( δ 1 , δ 2 ) (\delta_1, \delta_2) ( δ 1 , δ 2 ) 픽셀 값 과 ( δ 1 , δ 2 ) (\delta_1, \delta_2) ( δ 1 , δ 2 ) 필터 값 을 곱하는 과정을 모든 shift 에 대해 반복하고 총합해서 마지막에 bias 를 더한다.
Absolute positional encoding
A q , k a b s = ( X q , : + P q , : ) W q r y W k e y T ( X k , : + P k , : ) T A^{abs}_{q, k} = (X_{q,:}+P_{q,:})W_{qry}W^T_{key}(X_{k,:}+P_{k,:})^T A q , k a b s = ( X q , : + P q , : ) W q r y W k e y T ( X k , : + P k , : ) T
= X q , : W q r y W k e y T X k , : T + X q , : W q r y W k e y T P k , : T + P q , : W q r y W k e y T X k , : T + P q , : W q r y W k e y T P k , : T \,\,\,\,\,\,\,\,\,\,\,\,=X_{q,:}W_{qry}W^T_{key}X^T_{k,:} + X_{q,:}W_{qry}W^T_{key}P^T_{k,:}+P_{q,:}W_{qry}W^T_{key}X^T_{k,:}+P_{q,:}W_{qry}W^T_{key}P^T_{k,:} = X q , : W q r y W k e y T X k , : T + X q , : W q r y W k e y T P k , : T + P q , : W q r y W k e y T X k , : T + P q , : W q r y W k e y T P k , : T
이 방식은 학습과 평가에서 사용할 수 있는 문장의 최대 길이가 정해져 있다는 문제가 있다.
Relative positional encoding
일련의 과정을 지나 최종 수식을 도출해낸다.
(1) 토큰 사이의 거리 k − q k-q k − q
A q , k r e l = ( X q , : + P q , : ) T W q r y T W k e y ( X k , : + P k − q ) A^{rel}_{q, k} = (X_{q,:}+\textcolor{red}{\sout{P_{q,:}}})^TW_{qry}^TW_{key}(X_{k,:}+P_{\textcolor{red}{k-q}}) A q , k r e l = ( X q , : + P q , : ) T W q r y T W k e y ( X k , : + P k − q )
= X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W k e y P k , : + P q , : T W q r y T W k e y X k , : + P q , : T W q r y T W k e y P k , : \,\,\,\,\,\,\,\,\,\,\,\,=X_{q,:}^TW_{qry}^TW_{key}X_{k,:} + X_{q,:}^TW_{qry}^TW_{key}P_{k,:}+\textcolor{red}{\sout{P_{q,:}^TW_{qry}^T}}W_{key}X_{k,:}+\textcolor{red}{\sout{P_{q,:}^TW_{qry}^T}}W_{key}P_{k,:} = X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W k e y P k , : + P q , : T W q r y T W k e y X k , : + P q , : T W q r y T W k e y P k , :
(2) P q , : T W q r y T P_{q,:}^TW_{qry}^T P q , : T W q r y T u , v u, v u , v
A q , k r e l = X q , : T W q r y T W k e y ( X k , : + P k − q ) A^{rel}_{q, k} = X_{q,:}^TW_{qry}^TW_{key}(X_{k,:}+P_{\textcolor{red}{k-q}}) A q , k r e l = X q , : T W q r y T W k e y ( X k , : + P k − q )
= X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W k e y P k − q + u T W k e y X k , : + v T W k e y P k − q \,\,\,\,\,\,\,\,\,\,\,\,=X_{q,:}^TW_{qry}^TW_{key}X_{k,:} + X_{q,:}^TW_{qry}^TW_{key}P_{\textcolor{red}{k-q}}+\textcolor{red}{u^T}W_{key}X_{k,:}+\textcolor{red}{v^T}W_{key}P_{\textcolor{red}{k-q}} = X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W k e y P k − q + u T W k e y X k , : + v T W k e y P k − q
(3) k − q k-q k − q δ \delta δ P k − q P_{k-q} P k − q r δ r_{\delta} r δ
A q , k r e l = X q , : T W q r y T W k e y ( X k , : + r δ ) A^{rel}_{q, k} = X_{q,:}^TW_{qry}^TW_{key}(X_{k,:}+\textcolor{red}{r_{\delta}}) A q , k r e l = X q , : T W q r y T W k e y ( X k , : + r δ )
= X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W k e y r δ + u T W k e y X k , : + v T W k e y r δ \,\,\,\,\,\,\,\,\,\,\,\,=X_{q,:}^TW_{qry}^TW_{key}X_{k,:} + X_{q,:}^TW_{qry}^TW_{key}\textcolor{red}{r_{\delta}}+\textcolor{red}{u^T}W_{key}X_{k,:}+\textcolor{red}{v^T}W_{key}\textcolor{red}{r_{\delta}} = X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W k e y r δ + u T W k e y X k , : + v T W k e y r δ
(4) 토큰 임베딩을 이용하는 W k e y W_{key} W k e y W ^ k e y \widehat{W}_{key} W k e y
A q , k r e l = X q , : T W q r y T W k e y ( X k , : + r δ ) A^{rel}_{q, k} = X_{q,:}^TW_{qry}^TW_{key}(X_{k,:}+\textcolor{red}{r_{\delta}}) A q , k r e l = X q , : T W q r y T W k e y ( X k , : + r δ )
= X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W ^ k e y r δ + u T W k e y X k , : + v T W ^ k e y r δ \,\,\,\,\,\,\,\,\,\,\,\,=X_{q,:}^TW_{qry}^TW_{key}X_{k,:} + X_{q,:}^TW_{qry}^T\textcolor{blue}{\widehat{W}_{key}}\textcolor{red}{r_{\delta}}+\textcolor{red}{u^T}W_{key}X_{k,:}+\textcolor{red}{v^T}\textcolor{blue}{\widehat{W}_{key}}\textcolor{red}{r_{\delta}} = X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W k e y r δ + u T W k e y X k , : + v T W k e y r δ
3. Implementation
Theorem 1
N h N_h N h N h D h × D o u t N_hD_h\,\times\,D_{out} N h D h × D o u t D p ≥ 3 D_p\,\geq\,3 D p ≥ 3 N h × N h \sqrt{N_h}\,\times\,\sqrt{N_h} N h × N h m i n ( D h , D o u t ) min(D_h, D_{out}) m i n ( D h , D o u t )
Theorem 1의 보조 정리 Lemma 1은 다음과 같다.
Lemma 1
N h = K 2 N_h=K^2 N h = K 2 h e a d head h e a d M u l t i − h e a d s e l f − a t t e n t i o n Multi-head self-attention M u l t i − h e a d s e l f − a t t e n t i o n h e a d head h e a d C o n v Conv C o n v s h i f t shift s h i f t H e a d Head H e a d s o f t m a x ( A q , : ( h ) ) k = { 1 i f f ( h ) = q − k 0 o t h e r w i s e softmax(A_{q,:}^{(h)})_k=\left\{\begin{matrix} 1\,\,if\,\,f(h)=q-k\\ 0\,\,otherwise\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{matrix}\right. s o f t m a x ( A q , : ( h ) ) k = { 1 i f f ( h ) = q − k 0 o t h e r w i s e
어떤 K × K k e r n e l K\times K\,\,kernel K × K k e r n e l M H S A ( X ) = C o n v ( X ) MHSA(X)=Conv(X) M H S A ( X ) = C o n v ( X ) W v a l ( h ) W_{val}^{(h)} W v a l ( h )
Lemma 1의 중요한 가정은 Conv 필터의 shift와 Head의 Query, Key 사이의 거리가 같을 때만 스코어가 1이고 나머지는 0이라는 것이다.
실제로 이것이 가능함은 Lemma 2에서 증명하기 때문에 우선은 그렇다고 가정하고 Lemma 1을 증명하자.
Proof
S e l f − A t t e n t i o n ( X ) t , : : = s o f t m a x ( A t , : ) X W v a l Self-Attention(X)_{t,:}\,\,:=\,\,softmax(A_{t,:})XW_{val} S e l f − A t t e n t i o n ( X ) t , : : = s o f t m a x ( A t , : ) X W v a l
M H S A ( X ) : = c o n c a t [ S e l f − A t t e n t i o n h ( X ) ] W o u t + b o u t MHSA(X)\,\,:=\,\,concat[Self-Attention_h(X)]W_{out}\,+\,b_{out} M H S A ( X ) : = c o n c a t [ S e l f − A t t e n t i o n h ( X ) ] W o u t + b o u t h ∈ [ N h ] \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\scriptsize{h\in[N_h]} h ∈ [ N h ]
위의 두 식을 조합하면 M H S A ( X ) MHSA(X) M H S A ( X )
M H S A ( X ) : = b o u t + ∑ h ∈ [ N h ] s o f t m a x ( A ( h ) ) X W v a l ( h ) W o u t [ ( h − 1 ) D h + 1 : h D h + 1 ] MHSA(X)\,\,:=\,\,b_{out}\,+\,\sum_{h\in[N_h]}\,\,softmax(A^{(h)})XW_{val}^{(h)}W_{out}[(h-1)D_h\,+\,1\,:\,hD_h\,+\,1] M H S A ( X ) : = b o u t + ∑ h ∈ [ N h ] s o f t m a x ( A ( h ) ) X W v a l ( h ) W o u t [ ( h − 1 ) D h + 1 : h D h + 1 ]
각 h h h W v a l ( h ) W o u t [ ( h − 1 ) D h + 1 : h D h + 1 ] W_{val}^{(h)}W_{out}[(h-1)D_h\,+\,1\,:\,hD_h\,+\,1] W v a l ( h ) W o u t [ ( h − 1 ) D h + 1 : h D h + 1 ] W ( h ) W^{(h)} W ( h )
M H S A ( X ) : = b o u t + ∑ h ∈ [ N h ] s o f t m a x ( A ( h ) ) X W ( h ) MHSA(X)\,\,:=\,\,b_{out}\,+\,\sum_{h\in[N_h]}\,\,softmax(A^{(h)})XW^{(h)} M H S A ( X ) : = b o u t + ∑ h ∈ [ N h ] s o f t m a x ( A ( h ) ) X W ( h )
지금은 인풋 X X X
각각의 토큰 q q q
M H S A ( X ) q : = ∑ h ∈ [ N h ] ( ∑ k s o f t m a x ( A q , : ( h ) ) k X k , : ) W ( h ) + b o u t MHSA(X)_q\,\,:=\,\,\sum_{h\in[N_h]}\,(\sum_k\,softmax(A_{q,:}^{(h)})_kX_{k,:})W^{(h)}\,+\,b_{out} M H S A ( X ) q : = ∑ h ∈ [ N h ] ( ∑ k s o f t m a x ( A q , : ( h ) ) k X k , : ) W ( h ) + b o u t
위 식에 Lemma 1을 반영하면 모든 k k k k = q − f ( h ) k=q-f(h) k = q − f ( h )
M H S A ( X ) q : = ∑ h ∈ [ N h ] X q − f ( h ) , : W ( h ) + b o u t MHSA(X)_q\,:=\,\sum_{h\in[N_h]}\,X_{q-f(h),:}W^{(h)}\,+\,b_{out} M H S A ( X ) q : = ∑ h ∈ [ N h ] X q − f ( h ) , : W ( h ) + b o u t
이 최종 결과를 다음과 같이 해석해보면,
h ∈ [ N h ] h\in[N_h] h ∈ [ N h ] X q − f ( h ) X_{q-f(h)} X q − f ( h ) W ( h ) W^{(h)} W ( h )
C o n v o l u t i o n l a y e r Convolution \,\,layer C o n v o l u t i o n l a y e r q q q
이로써, 특정 상황에서 m u l t i − h e a d s e l f a t t e n t i o n multi-head\,\, self\,\, attention m u l t i − h e a d s e l f a t t e n t i o n C o n v o l u t i o n Convolution C o n v o l u t i o n L e m m a 1 Lemma \,\,1 L e m m a 1
Lemma 2
모든 △ ∈ △ K \bigtriangleup \in \bigtriangleup_K △ ∈ △ K k − q = △ k-q=\bigtriangleup k − q = △ s o f t m a x ( A q , : ( h ) ) k = 1 softmax(A_{q,:}^{(h)})_k=1 s o f t m a x ( A q , : ( h ) ) k = 1 v v v
Relative positional encoding r δ ( D p ≥ 3 ) , W q r y , W k e y , W ^ k e y , u r_\delta(D_p\geq 3), W_{qry}, W_{key}, \widehat{W}_{key}, u r δ ( D p ≥ 3 ) , W q r y , W k e y , W k e y , u
Proof
A q , k r e l = X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W ^ k e y r δ + u T W k e y X k , : + v T W ^ k e y r δ A^{rel}_{q,k}=X^T_{q,:}W^T_{qry}W_{key}X_{k,:}+X^T_{q,:}W^T_{qry}\widehat{W}_{key}r_\delta+u^TW_{key}X_{k,:}+v^T\widehat{W}_{key}r_\delta A q , k r e l = X q , : T W q r y T W k e y X k , : + X q , : T W q r y T W k e y r δ + u T W k e y X k , : + v T W k e y r δ
W q r y = W k e y = 0 , W ^ k e y = I ( i d e n t i t y m a t r i x ) W_{qry}=W_{key}=0,\,\,\widehat{W}_{key}=I\,\,(identity\,\,matrix) W q r y = W k e y = 0 , W k e y = I ( i d e n t i t y m a t r i x )
그러면, A q , k r e l = v T r δ w h e r e δ : = k − 1 A^{rel}_{q,k}=v^Tr_\delta\,\,where\,\,\delta:=k-1 A q , k r e l = v T r δ w h e r e δ : = k − 1
A q , k r e l = − α ( ∣ ∣ δ − △ ∣ ∣ 2 + c ) A^{rel}_{q,k}=-\alpha(||\delta-\bigtriangleup||^2+c) A q , k r e l = − α ( ∣ ∣ δ − △ ∣ ∣ 2 + c ) △ \bigtriangleup △ C o n v Conv C o n v s h i f t shift s h i f t
그러면 softmax attention 식은 다음과 같다.s o f t m a x ( A q , : ) k = e − α ( ∣ ∣ δ − △ ∣ ∣ 2 + c ) ∑ k ′ e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 + c ) softmax(A_{q,:})_k={e^{-\alpha(||\delta-\bigtriangleup||^2+c)}\over \sum_{k'}e^{-\alpha(||(k'-q)-\bigtriangleup||^2+c)}} s o f t m a x ( A q , : ) k = ∑ k ′ e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 + c ) e − α ( ∣ ∣ δ − △ ∣ ∣ 2 + c )
α \alpha α lim α → ∞ s o f t m a x ( A q , : ) k = lim α → ∞ e − α ( ∣ ∣ δ − △ ∣ ∣ 2 + c ) ∑ k ′ e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 + c ) \underset{\alpha \to \infty}{\lim}\,softmax(A_{q,:})_k=\underset{\alpha \to \infty}{\lim}\,{e^{-\alpha(||\delta-\bigtriangleup||^2+c)}\over \sum_{k'}e^{-\alpha(||(k'-q)-\bigtriangleup||^2+c)}} α → ∞ lim s o f t m a x ( A q , : ) k = α → ∞ lim ∑ k ′ e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 + c ) e − α ( ∣ ∣ δ − △ ∣ ∣ 2 + c )
이 경우 분모와 분자에 모두 있는 상수 c c c lim α → ∞ s o f t m a x ( A q , : ) k = lim α → ∞ e − α ( ∣ ∣ δ − △ ∣ ∣ 2 ) ∑ k ′ e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 ) \underset{\alpha \to \infty}{\lim}\,softmax(A_{q,:})_k=\underset{\alpha \to \infty}{\lim}\,{e^{-\alpha(||\delta-\bigtriangleup||^2)}\over \sum_{k'}e^{-\alpha(||(k'-q)-\bigtriangleup||^2)}} α → ∞ lim s o f t m a x ( A q , : ) k = α → ∞ lim ∑ k ′ e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 ) e − α ( ∣ ∣ δ − △ ∣ ∣ 2 )
δ \delta δ △ \bigtriangleup △
F o r δ = △ , For\,\,\delta=\bigtriangleup, F o r δ = △ ,
lim α → ∞ s o f t m a x ( A q , : ) k = lim α → ∞ 1 1 + ∑ k ′ ≠ k e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 ) \underset{\alpha \to \infty}{\lim}\,softmax(A_{q,:})_k=\underset{\alpha \to \infty}{\lim}\,{1\over 1+\sum_{k'\neq k}e^{-\alpha(||(k'-q)-\bigtriangleup||^2)}} α → ∞ lim s o f t m a x ( A q , : ) k = α → ∞ lim 1 + ∑ k ′ = k e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 ) 1
분자는 e − α × 0 e^{-\alpha\times 0} e − α × 0 k = k ′ k=k' k = k ′ e − inf × ⋅ ⋅ ⋅ = 0 e^{-\inf\times \cdot\cdot\cdot}=0 e − i n f × ⋅ ⋅ ⋅ = 0 1 1 = 1 {1 \over 1}=1 1 1 = 1
F o r δ ≠ △ , For\,\,\delta\neq\bigtriangleup, F o r δ = △ ,
lim α → ∞ s o f t m a x ( A q , : ) k = lim α → ∞ e − α ( ∣ ∣ δ − △ ∣ ∣ 2 ) ∑ k ′ e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 ) \underset{\alpha \to \infty}{\lim}\,softmax(A_{q,:})_k=\underset{\alpha \to \infty}{\lim}\,{e^{-\alpha(||\delta-\bigtriangleup||^2)}\over \sum_{k'}e^{-\alpha(||(k'-q)-\bigtriangleup||^2)}} α → ∞ lim s o f t m a x ( A q , : ) k = α → ∞ lim ∑ k ′ e − α ( ∣ ∣ ( k ′ − q ) − △ ∣ ∣ 2 ) e − α ( ∣ ∣ δ − △ ∣ ∣ 2 )
분자는 e − inf × ⋅ ⋅ ⋅ e^{-\inf\times \cdot\cdot\cdot} e − i n f × ⋅ ⋅ ⋅ k = k ′ k=k' k = k ′ e − inf × ⋅ ⋅ ⋅ = 0 e^{-\inf\times \cdot\cdot\cdot}=0 e − i n f × ⋅ ⋅ ⋅ = 0 0 1 = 0 {0 \over 1}=0 1 0 = 0
이제, attention score의 값이 α ( ∣ ∣ δ − △ ∣ ∣ 2 + c ) \alpha(||\delta-\bigtriangleup||^2+c) α ( ∣ ∣ δ − △ ∣ ∣ 2 + c ) v v v r δ r_\delta r δ L e m m a 2 Lemma\,\,2 L e m m a 2
v = − α ( 1 , − 2 △ 1 , − 2 △ 2 ) , v\,=\,-\alpha(1, -2\bigtriangleup_1, -2\bigtriangleup_2), v = − α ( 1 , − 2 △ 1 , − 2 △ 2 ) , r δ = ( ∣ ∣ δ ∣ ∣ 2 , δ 1 , δ 2 ) r_\delta\,=\,(||\delta||^2,\delta_1,\delta_2) r δ = ( ∣ ∣ δ ∣ ∣ 2 , δ 1 , δ 2 )
그러면,A q , k = v T r δ A_{q,k}=v^Tr_\delta A q , k = v T r δ = − α ( ∣ ∣ δ ∣ ∣ 2 − 2 △ 1 δ 1 − 2 △ 2 δ 2 ) \,\,\,\,\,\,\,\,\,\,\,\,=-\alpha(||\delta||^2-2\bigtriangleup_1\delta_1-2\bigtriangleup_2\delta_2) = − α ( ∣ ∣ δ ∣ ∣ 2 − 2 △ 1 δ 1 − 2 △ 2 δ 2 ) = − α ( ∣ ∣ δ ∣ ∣ 2 − 2 < δ , △ > ) \,\,\,\,\,\,\,\,\,\,\,\,=-\alpha(||\delta||^2-2<\delta, \bigtriangleup>) = − α ( ∣ ∣ δ ∣ ∣ 2 − 2 < δ , △ > ) = − α ( ∣ ∣ δ − △ ∣ ∣ 2 − ∣ ∣ △ ∣ ∣ 2 ) \,\,\,\,\,\,\,\,\,\,\,\,=-\alpha(||\delta-\bigtriangleup||^2-||\bigtriangleup||^2) = − α ( ∣ ∣ δ − △ ∣ ∣ 2 − ∣ ∣ △ ∣ ∣ 2 ) = − α ( ∣ ∣ δ ∣ ∣ 2 + c ) w h e n c = − ∣ ∣ △ ∣ ∣ 2 \,\,\,\,\,\,\,\,\,\,\,\,=-\alpha(||\delta||^2+c)\,\,when\,\,c=-||\bigtriangleup||^2 = − α ( ∣ ∣ δ ∣ ∣ 2 + c ) w h e n c = − ∣ ∣ △ ∣ ∣ 2