[논문 요약] Self-Attention Generative Adversarial Networks

1. Introduction

최근 Image synthesis의 동향

• GAN의 등장으로 많은 진보가 이루어졌다
• 특히, Deep Convolutional networks를 이용한 GAN이 성공적인 모습을 보여주었다
• multi-class dataset으로 학습했을 때 몇몇 class의 image를 생성하는 것에 어려움을 보였다
  (바다, 하늘처럼 주로 질감 으로 표현되는 class는 잘 생성하지만 강아지의 명확한 발 모양처럼 기하학적이나 구조적인 특징을 갖는 class 생성이 어렵다)

하지만, 기존 모델은 Convolution에 지나치게 의존했다는 문제가 있다.

Convolution의 문제점

• 멀리 떨어져 있는 값들 간의 dependency는 여러 convolutional layer를 지나야 계산된다
• 작은 모델은 long term dependency 를 계산 할 만큼 layer 가 깊지 않을 수 있다
• Dependency 를 인식 하기 위해 여러 layer들을 섬세히 조절하는 파라미터를 찾기 어렵다
• 커널의 크기를 늘리면 그전보다 계산적, 통계적 측면에서 비효율적이게 된다

이 문제는 Self-attention으로 해결할 수 있다

• Long-range dependency를 잘 인식하면서도 효율성을 갖춘다
• 한 위치에서의 결과값을 계산하기 위해 다른 모든 위치에서의 feature들의 weighted sum을 이용한다

연구진은 이와 같은 이점을 활용하고자 Convolutional GAN에 Self-attention을 결합해 SAGAN을 만들었다.

• Generator : 모든 위치에서의 섬세한 detail이 다른 위치에서의 detail과 잘 연관된 이미지를 생성할 수 있다
• Discriminator : 이미지를 전체적으로 보았을 때 알 수 있는 복잡한 기하학적 특징을 검출해낼 수 있다

2. Related Work

GAN

• Image-to-Image translation, Image super-resolution, text-to-image synthesis를 비롯한 이미지 합성 task에서 굉장한 성공을 거두었다
• 학습이 불안정하고 hyper parameter에 민감하게 반응하는 경향이 있다

연구진은 Spectral normalization과 Projection 기반의 Discriminator를 결합하여 성능을 크게 향상시킨 연구에 주목했다

Spectral Normalization

Training criterion for Discriminator
$V(G,D) = \int_xp_{data}(x)log(D(x))dx + \int_xp_z(z)log(1-D(g(z)))dz$

$= \int_xp_{data}(x)log(D(x))dx+p_g(x)log(1-D(x))dx$

Discriminator function
$D^*_G(x) = {{p_{data}(x)}\over{p_{data}(x)+p_g(x)}}$ $\because alog(x) + blog(1-x)$는 $x={a}\over{a+b}$일때 최대

${{p_{data}(x)}\over {p_{data(x)+p_g(x)}}} = {1\over{1+{p_g(x)\over{p_{data}(x)}}}}={1\over{1+e^{log ({{p_g(x)}\over p_{data}(x)})}}}$

$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,={1\over{1+e^{-(log ({p_{data}(x)})-log({p_g(x)}))}}}$

$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=sigmoid(log(p_{data}(x))-log(p_g(x)))$

위와 같은 과정으로 아래 수식으로도 변형이 가능하다.

$D^*_G(x) = sigmoid(f^*(x)), where f^*(x)=log(q_{data}(x))-log(P_G(x))$

학습을 위해 Discriminator function의 gradient를 구하면 다음과 같다.

$\bigtriangledown_xf^*(x)={\partial f^*(x)\over \partial x}={1\over\ q_{data}(x)}\bigtriangledown_x q_{data}(x)-{1\over{p_G(x)}}\bigtriangledown_x P_G(x)$

이때, 미분 값이 무한정 커질 수 있기 때문에 굉장히 큰 gradient가 도출되는 경우 학습에 문제가 생길 수 있다.

연구진은 Weight normalization을 통해 립시츠 상수를 제한하는 방식으로 이 문제를 해결했다.

립시츠 상수란?

${|f(x)-f(y)|\over |x-y|}<=K$를 만족하는 $K$의 최솟값

$y=sin\,x$의 립시츠 상수 K는 1이다.

Spectral Normalization을 통해 Discrimination function의 립시츠 상수를 1 이하로 제한하면 gradient가 과도하게 높아지는 것을 방지해 학습을 안정시킬 수 있다.

구체적인 방법은 뒤에서 다시 다루도록 한다.

Attention models

• Global dependency를 인식하기 위해 필수적인 기법이다
• 기계 번역 모델이 self-attention 기법만으로 SOTA 성능을 달성할 수 있다는 것이 증명되었다
• 컴퓨터 비전 분야에서도 self-attention을 이용해 이미지를 생성한 사례가 있다

하지만, 아직까지 self-attention이 GAN에 적용된 사례는 없기 때문에 연구진은 본 연구를 진행하게 되었다.

3. Implementation

SAGAN과 Transformer는 둘 다 self-attention을 사용하기 때문에 어떤 점이 유사한지 비교하며 진행하도록 한다.

먼저, Transformer의 self-attention에 대해 알아보자.

I study at school 이라는 문장을 인풋으로 받으면, 그림과 같이 각각의 Weight를 곱해 Query, Key, Value 맵이 만들어진다.

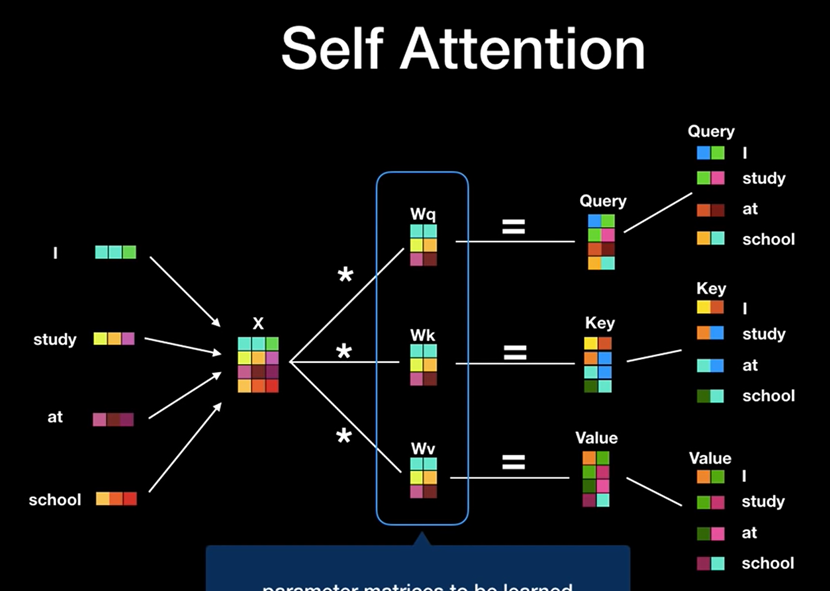
이중에 우선 I 의 Query 벡터와 모든 단어들의 Key 벡터들에 집중해보자.

I 의 Query 벡터에 각 단어들의 Key 벡터들을 곱하면 모델이 I 라는 단어를 생성할 때 각 단어에 관심을 갖는 정도를 계산할 수 있다.

이번에는 단어들의 Value 벡터들에 집중해보자.

방금 구한 각 단어들의 softmax값에 그 단어가 문장에서 독자적으로 갖는 중요도를 뜻하는 Value 벡터를 곱하면 Attention layer의 output이 나온다.

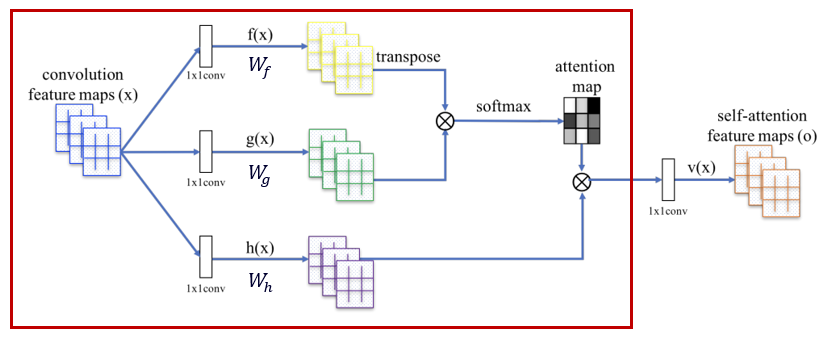
SAGAN도 Transformer와 굉장히 유사한 작업을 한다.

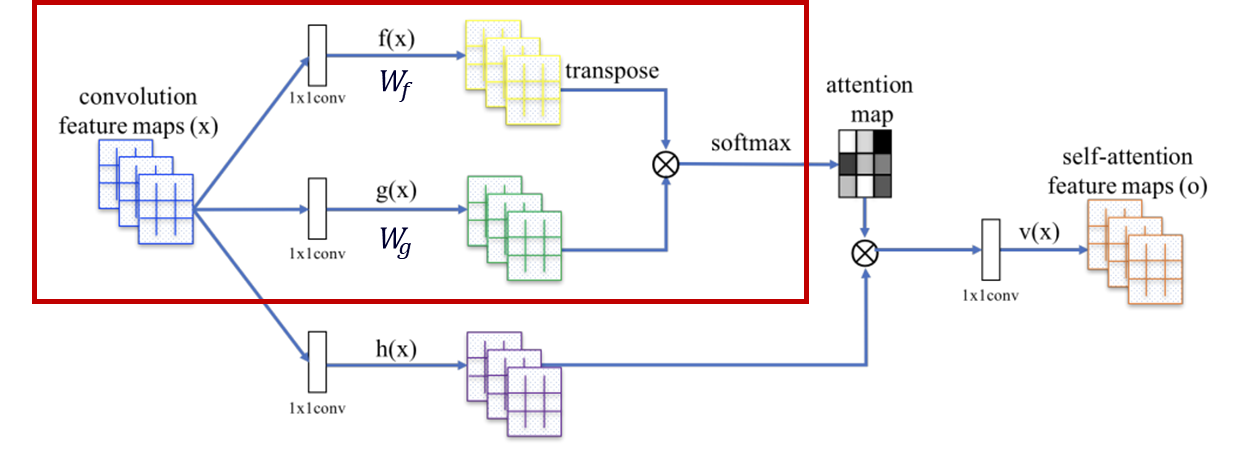
우선 빨간색 박스 부분을 보자.

$\beta_{j, i}={exp(s_{ij})\over \sum_{i=1}^N exp(s_{ij})},\, where\, s_{ij}=f(x_i)^Tg(x_j)$

위 수식은 모델이 $j$번째 픽셀을 생성할 때 $i$번째 픽셀에 관심을 갖는 정도를 계산한다.

이는 Transformer에서 'I'라는 단어의 Query에 각 단어들의 Key를 곱한 것과 유사한 기능을 한다고 볼 수 있다.

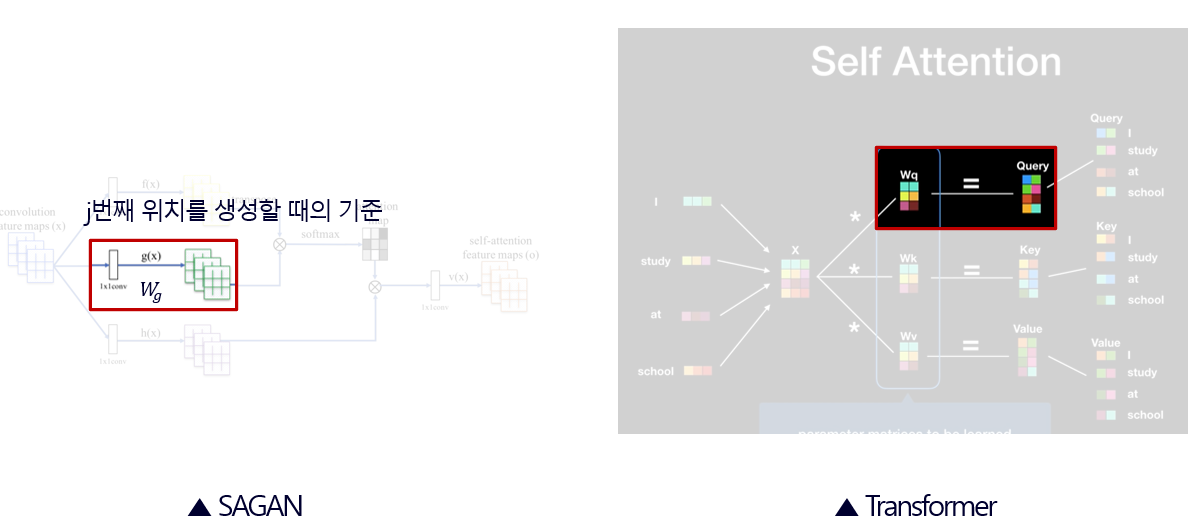
구조적으로 보면, $j$번째 픽셀을 생성할 때의 기준을 부여해주는
$W_g$는 Transformer의 Query로 볼 수 있다.

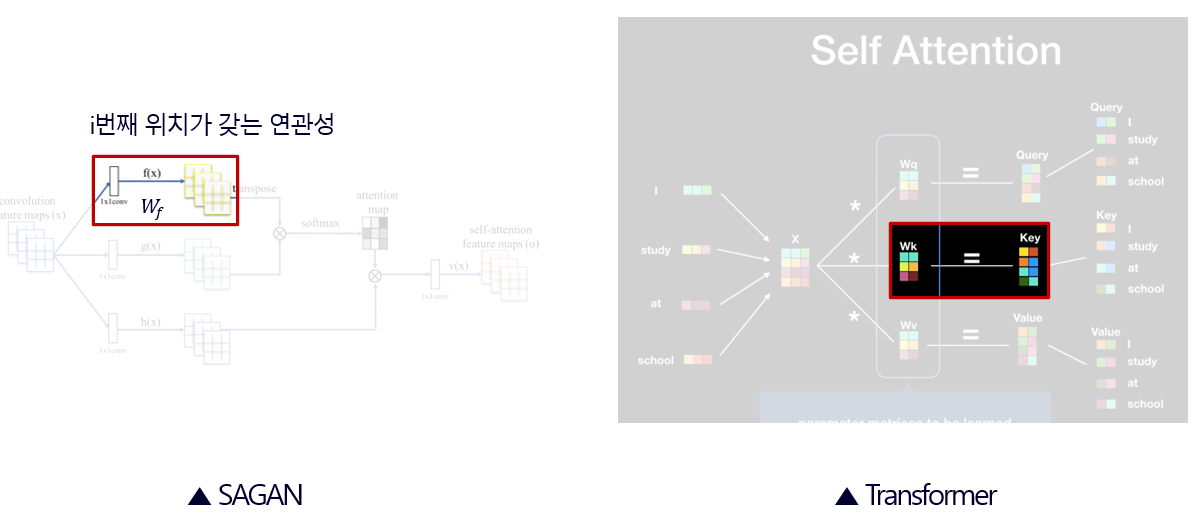
그리고 $j$번째 픽셀에 대해 $i$번째 픽셀이 갖는 연관성을 부여해주는 $W_f$는 Transformer의 Key로 볼 수 있다.

방금 전까지의 과정을 모든 $j$와 $i$에 대해 반복하면 attention map을 얻을 수 있다.

$o_j = v\,(\sum_{i=1}^N \beta_{j,i}\,h(x_i)), \,h(x_i)=W_hx_i, \,v(x_i)=W_vx_i$

$W_h$ : 이미지에서 $i$번째 픽셀이 갖는 중요도

최종적으로 모든 $i$에 대한 attention값과 중요도를 곱해준 값을 총합 한 뒤 추가로 $W_v$ 행렬을 곱하면 self-attention feature map을 구할 수 있다.

이 과정은 Transformer에서 'I'라는 단어에 대한 각 단어들의 softmax 값들에 그 단어가 문장에서 갖는 중요도를 곱하고 총합하는 것과 유사하다.

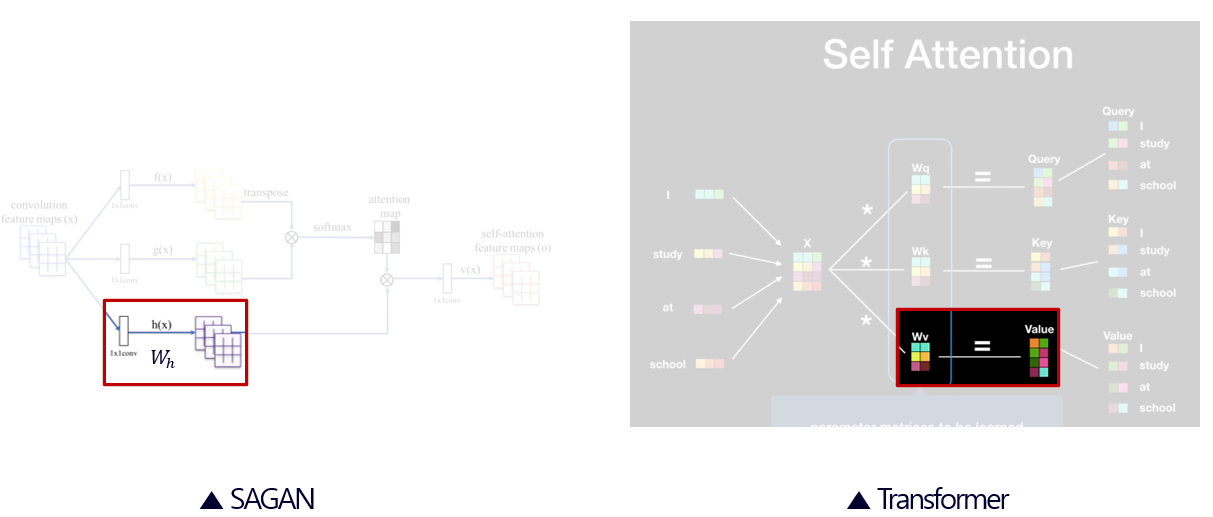
따라서 구조적으로 보면 이미지에서 $i$번째 픽셀이 갖는 중요도를 부여하는 $W_h$는 Transformer의 Value로 볼 수 있다.

채널 개수

이미지의 Query, Key, Value 값들을 검출해내는 $W_g,\,W_f,\,W_h$는 인풋 $x$의 채널 개수보다 적은 개수의 채널을 출력한다.

이것은 attention을 처리할 때의 메모리 효율성을 위한 것으로, 실험 결과 $x$의 채널을 $1\over 8$배로 줄여도 큰 성능차이가 없었다고 한다.

$\bold {W_g}\,\in \mathbb{R}^{\overline{C}\times C}, \,\bold {W_f}\,\in \mathbb{R}^{\overline{C}\times C}$

$C$ : Feature map $x$의 output 채널 개수
$\overline{C}$ : Query, Key layer의 output 채널 개수

학습 공식

$y_i = \gamma o_i + x_i$

Self-attention feature map은 그 다음 layer의 인풋으로 들어갈 때 학습 가능한 파라미터 $\gamma$로 scale되고 이전 convolution layer의 element $x_i$가 더해진다.

$\gamma$는 처음에 0으로 초기화되고 이후 학습을 통해 점차 증가하는데, 연구진은 이를 통해 처음에는 간단한 task($x_i$의 local한 정보)를 학습하고 점차 복잡한 task(이미지의 global한 정보)를 학습하는 것을 의도했다.

4. Stabilization

Spectral Normalization

립시츠 상수

${|f(x)-f(y)|\over |x-y|}<=K$ 를 만족하는 $K$의 최솟값

Discriminator 함수의 한 layer $f$의 립시츠 상수

$f$의 Weight 행렬 = $W$

${|f(x)-f(y)|\over|x-y|}={|Wx-Wy|\over|x-y|}={|Wh|\over|h|}\leq K$ 를 만족하는 $K$의 최솟값

특이값 분해 (SVD)

$A=U\Sigma V^T$

Left singular vector $U$의 열 벡터 $u_i$
Right singular vector $V$의 열 벡터 $v_i$
Singular values $\Sigma$의 대각 원소 $\sigma_i$

$Av_i=\sigma_i u_i$

$W = U\Sigma V^T$

$Wv_i = \sigma_i u_i$

$Let\,\, \sigma_n\,\, is\,\, largest\,\, singular\,\, value,\,\, then$

${|Wh|\over |h|} \leq {|Wv_n|\over |v_n|}={|\sigma_nu_n|\over|v_i|}=|\sigma_n|$

$\therefore$ $\,g$의 립시츠 상수는 $W$의 가장 큰 signular value (spectral norm)이다.

Spectral Normalization

Discriminator 함수의 각 layer의 $W$ 행렬을 그것의 Spectral norm으로 나누어 준다.

$\overline{W}={W\over \sigma(W)}\,\,\,\,$ ($\sigma(W)=W$의 가장 큰 singular value)

추가로, 이전 연구들에서는 Discriminator에서만 spectral normalization을 시행했는데 연구진은 Generator에 대해서도 시행했다.

문제점

Regularization은 GAN의 학습이 느려지는 문제를 발생시켰다.
정규화된 Discriminator는 Generator의 한 업데이트 당 여러 번의 업데이트 step이 필요했기 때문이다.
연구진은 TTUR에 대한 연구결과를 차용해 Discriminator와 Generator의 학습률을 다르게 하여 이 문제를 해결했다.

TTUR(Two Time-Scale Update Rule)

• Discriminator를 regularize하면 GAN의 학습이 느려지는 현상이 발생
• Regularize된 Discriminator는 Generator의 한 업데이트 당 여러 번의 업데이트 step이 필요하게 됨
• Discriminator의 학습률을 높여 더 적은 업데이트 step만으로도 수렴할 수 있도록 유도함

5. Experiments

Evaluate Stabilization techniques

첫 번째 실험은 GAN의 학습을 안정화하기 위해 도입한 Spectal Normalization과 TTUR의 효능을 평가하기 위한 실험이다.

FID : 생성 이미지와 실제 이미지의 특징 분포를 비교하는 지표
IS(Inception Score) : 생성된 이미지의 품질과 다양성을 평가하는 지표

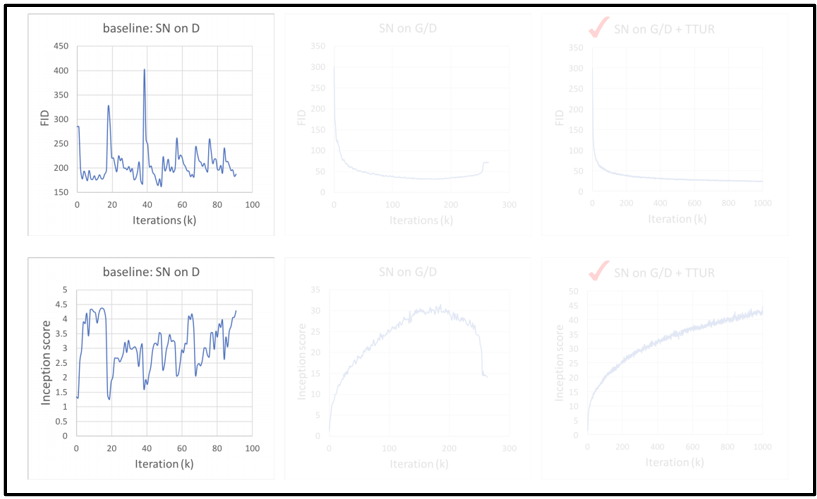
Discriminator에만 Spectral Normalization을 시행했을 때는 작은 iteration에서부터 mode collapse가 일어났다.
Generator가 Discriminator를 속이기 위해 비슷한 이미지만 생성해내기 때문에 평가 지표가 진동하는 모습을 확인할 수 있다.

이때 생성된 이미지 샘플은 다음과 같다.

유사한 이미지가 색깔이나 질감만 바뀐 채 여러번 생성되는 것을 볼 수 있다.

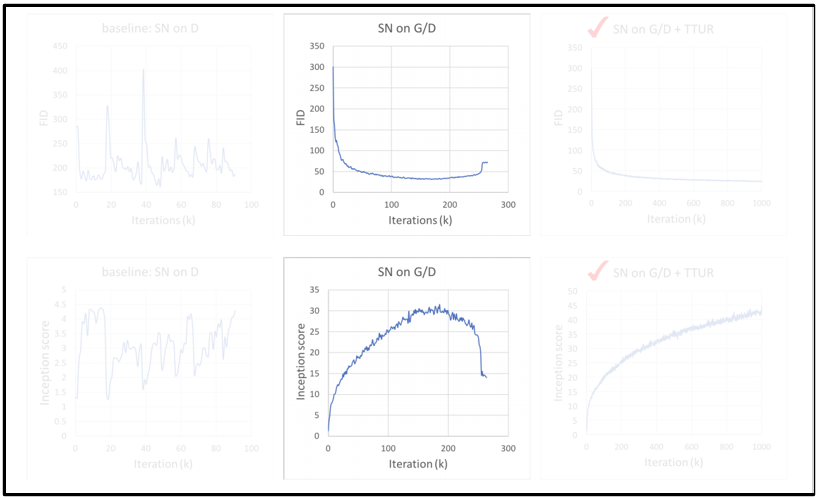
다음으로, Generator와 Discriminator 모두에 Spectral normalization을 시행했을 때의 지표이다.
비교적 안정적인 학습이 이루어지지만 260번째 iteration부터 성능이 다시 나빠지기 시작하는 현상을 볼 수 있다.

이때 생성된 이미지 샘플은 다음과 같다.

앞서 보았던 이미지들보다 비교적 실제 같고 다양한 샘플이 생성된 것을 확인할 수 있다.

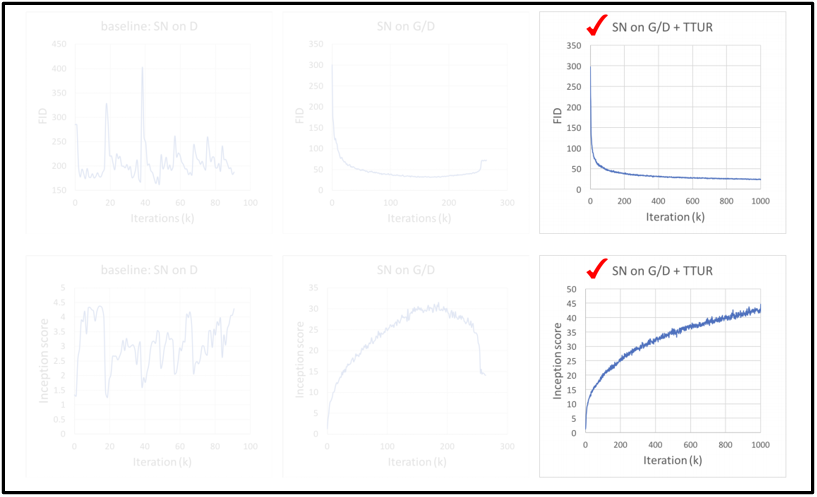
마지막으로 Discriminator와 Generator의 학습률을 다르게 주는 TTUR 기법을 추가했을 때의 지표이다.
확실히 앞선 지표들보다 안정적으로 학습이 이루어지는 모습을 확인할 수 있다.

이때 생성된 이미지 샘플은 다음과 같다.

확실히 더 명확하고 다양한 이미지가 생성되는 것을 확인할 수 있다.

Evaluate Self-attention mechanism

• 더 넓은 feature map에 self-attention을 시행할수록 더 많은 정보를 얻을 수 있고 영역 간의 상관관계를 더 자유롭게 학습할 수 있다
• 같은 크기의 Residual map으로 대체하면 불안정해지거나 성능이 나빠졌기 때문에 SAGAN의 효능이 단순히 모델의 depth나 capacity가 증가했기 때문이 아님을 알 수 있다

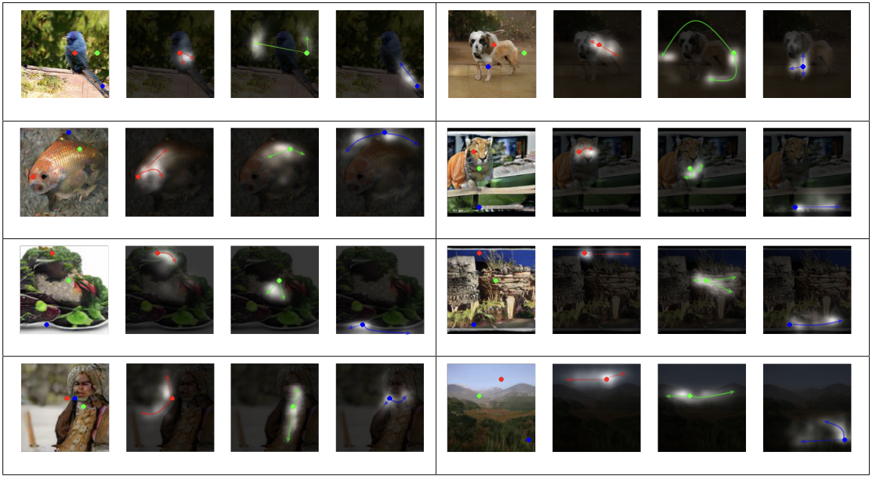
연구진은 Self-attention의 기능을 시각적으로 표현하기 위해 output과 가장 근접한 마지막 layer에 self-attention을 시행하고 그것의 출력값을 나타냈다.

몇가지 이미지를 해석해보면 다음과 같다.

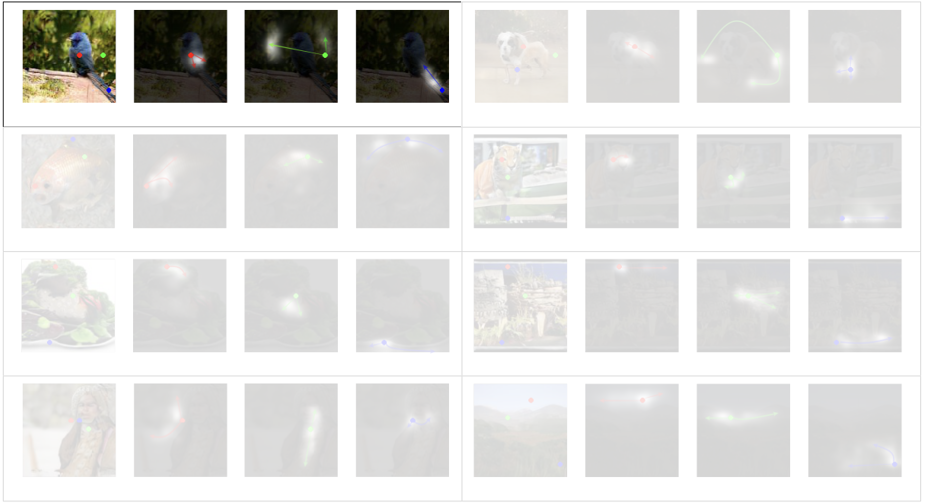
• 각각의 빨간색, 초록색, 파란색 Query에 대해서 인접한 위치보다는 비슷한 색깔과 질감에 attention한다.

• 근처에 있는 Query들도 서로 다른 곳에 attention할 수 있다.

• 강아지의 다리들이 확실하게 분리되어 생성되었다
• attention이 접합된 영역의 뼈대를 이어주어 구조를 알 수 있도록 도와준다

Evaluation with SOTA

마지막 실험은 SOTA 모델과 SAGAN의 성능을 비교해보는 실험이다.
Inception Score와 FID 모두에서 SAGAN이 우수한 점수를 얻었음을 알 수 있다.

이 샘플들은 SAGAN이 SOTA보다 좋은 점수를 받은 Class들을 생성한 이미지들이다.

금붕어, 새의 깃털 무늬, 세인트 버나드 종과 살쾡이의 얼굴 무늬처럼 복잡한 구조적 패턴 학습에 뛰어난 모습을 보이는 것을 확인할 수 있다.

반면 돌벽, 간헐천, 골짜기, 산호초처럼 단순한 패턴 학습에는 이점을 보이지 않는 것을 알 수 있다.

마지막으로 결론을 지어보자면 다음과 같다.

6. Conclusion

아이디어적 측면

• Self-attention 매커니즘을 GAN에 성공적으로 통합시켰다

안정화적 측면

• Generator에도 Spectral Normalization을 적용하는 것의 이점을 증명했다
• TTUR이 regularize된 Discriminator의 학습 속도를 높이는 것을 보여주었다

성능적 측면

• Long-range dependency를 인식하고 표현하는 것에 뛰어나다
• Class-conditional 이미지 생성 SOTA모델보다 높은 성능을 가졌다