3장 사이킷런을 타고 떠나는 머신 러닝 분류 모델 투어

3.1 분류 알고리즘 선택

☑️머신러닝 훈련 단계☑️
1) 특성을 선택하고 훈련 샘플을 모으기
2) 성능 지표를 선택
3) 분류 모델과 최적화 알고리즘 선택
4) 모델의 성능을 평가 (학습에 사용하는 데이터에 크게 의존)
5) 알고리즘을 튜닝

3.2 사이킷런 첫걸음: 퍼셉트론 훈련

🟡 150개의 꽃 샘플
🟡 특성 행렬 X : 꽃잎 길이, 꽃잎 너비
🟡 벡터 y : 꽃 품종에 해당하는 클래스 레이블


☑️사이킷런에서 붓꽃 데이터셋을 적재☑️

from sklearn import datasets
import numpy as np

iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target

# np.uniuqe(y) : iris.target에 저장된 세 개의 고유한 클래스 레이블 반환
print('클래스 레이블:', np.unique(y))

➡️ 클래스 레이블 정수로 인코딩 -> 계산 성능 향상 위함

☑️훈련된 모델 성능 평가 -> 훈련 데이터셋과 테스트 데이터셋으로 분할☑️

• 30% : 테스트 데이터(45개의 샘플), 70% : 훈련 데이터(105개의 샘플)
• train_test_split 함수 : x와 y 배열을 랜덤하게 나눔
• random_state 매개변수 : 데이터셋 분할 전 무작위로 섞기 위한 난수 생성기
• stratify=y : 계층화(훈련 데이터셋과 테스트 데이터셋의 클래스 레이블 비율을 입력 데이터셋과 동일하게 만듦)

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=1, stratify=y)

☑️계층화 잘 되었는지 확인☑️

• bincount 함수 : 배열에 있는 고유한 값의 등장 횟수 파악

print('y의 레이블 카운트:', np.bincount(y))
print('y_train의 레이블 카운트:', np.bincount(y_train))
print('y_test의 레이블 카운트:', np.bincount(y_test))

☑️성능을 위해 특성 스케일 조정☑️

• 사이킷런 StandardScaler 클래스 : 특성을 표준화 해줌
• StandardScaler의 fit 메서드 : 훈련 데이터셋의 각 특성 차원마다 샘플 평균과 표준 편차 계산
• transform 메서드 : 계산된 샘플 평균과 표준 편차를 사용하여 훈련 데이터셋과 테스트 데이터셋을 표준화

from sklearn.preprocessing import StandardScaler

sc = StandardScaler() # 클래스 로드하여 sc 변수에 할당
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

☑️퍼셉트론 모델 훈련☑️

• OvR(One-versus-Rest) 방식을 사용하여 다중 분류를 지원
• 3개의 붓꽃 클래스를 퍼셉트론에 한 번에 주입
• eta0 : 학습률
• random_state 매개변수 : 에포크마다 훈련 데이터셋을 섞은 결과가 그대로 재현될 수 있게 함

from sklearn.linear_model import Perceptron

# Perceptron 클래스를 로드
ppn = Perceptron(eta0=0.1, random_state=1)
# fit 메서드로 모델 훈련
ppn.fit(X_train_std, y_train)

☑️모델로 예측해보기☑️

y_pred = ppn.predict(X_test_std)
print('잘못 분류된 샘플 개수: %d' % (y_test != y_pred).sum())

➡️ 퍼셉트론 모델이 45개의 샘플에서 한 개를 잘못 분류함
➡️ 테스트 데이터셋에 대한 분류 오차 : 약 0.022 또는 2.2%

☑️퍼셉트론의 분류 정확도 계산☑️

• metrics 모듈 : 다양한 성능 지표 포함
• y_test : 진짜 클래스 레이블
• y_pred : 앞서 예측한 클래스 레이블
• score 메서드 : 분류기의 예측 정확도 계산(predict 메서드와 accuracy_score 메서드를 연결하여 계산)
  📍 정확도란? => 1 - 오차

from sklearn.metrics import accuracy_score

print('정확도: %.3f' % accuracy_score(y_test, y_pred))
print('정확도: %.3f' % ppn.score(X_test_std, y_test))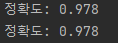

☑️퍼셉트론 모델의 결정 경계 그려서 시각화☑️

• plot_decision_regions 함수 : 퍼셉트론 모델의 결정 경계를 그려줌

from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt


def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):

    # 마커와 컬러맵을 설정합니다.
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # 결정 경계를 그립니다.
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0],
                    y=X[y == cl, 1],
                    alpha=0.8,
                    c=colors[idx],
                    marker=markers[idx],
                    label=cl,
                    edgecolor='black')

    # 테스트 샘플을 부각하여 그립니다.
    if test_idx:
        # 모든 샘플을 그립니다.
        X_test, y_test = X[test_idx, :], y[test_idx]

        plt.scatter(X_test[:, 0],
                    X_test[:, 1],
                    facecolor='none',
                    edgecolor='black',
                    alpha=1.0,
                    linewidth=1,
                    marker='o',
                    s=100,
                    label='test set')
        
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))

plot_decision_regions(X=X_combined_std, y=y_combined,
                      classifier=ppn, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')

plt.tight_layout()
# plt.savefig('images/03_01.png', dpi=300)
plt.show()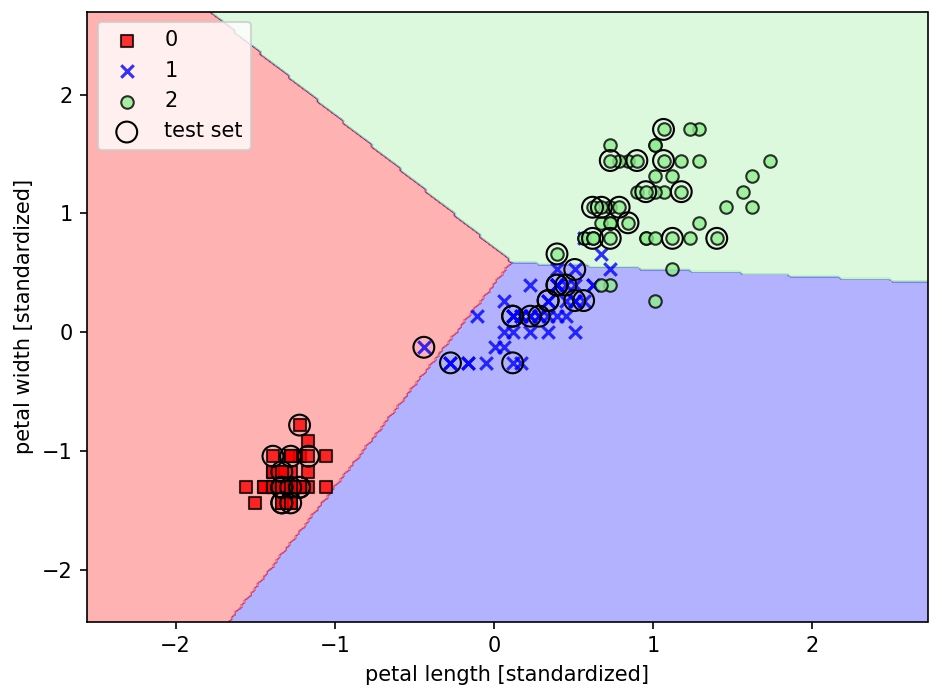

➡️ 3개의 붓꽃 클래스는 선형 결정 경계로 완벽하게 분류되지 ❌
➡️ 퍼셉트론 알고리즘은 선형적으로 구분되지 않는 데이터셋에는 수렴하지 ❌

3.3 로지스틱 회귀를 사용한 클래스 확률 모델링

3.3.1 로지스틱 회귀의 이해와 조건부 확률

로지스틱 회귀 : 구현이 쉽고 선형적으로 구분되는 클래스에 뛰어난 성능을 내는 분류 모델, 이진 분류를 위한 선형 모델

☑️시그모이드 함수 그려보기☑️

import matplotlib.pyplot as plt
import numpy as np


def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

z = np.arange(-7, 7, 0.1)
phi_z = sigmoid(z)

plt.plot(z, phi_z)
plt.axvline(0.0, color='k')
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')

# y 축의 눈금과 격자선
plt.yticks([0.0, 0.5, 1.0])
ax = plt.gca()
ax.yaxis.grid(True)

plt.tight_layout()
# plt.savefig('images/03_02.png', dpi=300)
plt.show()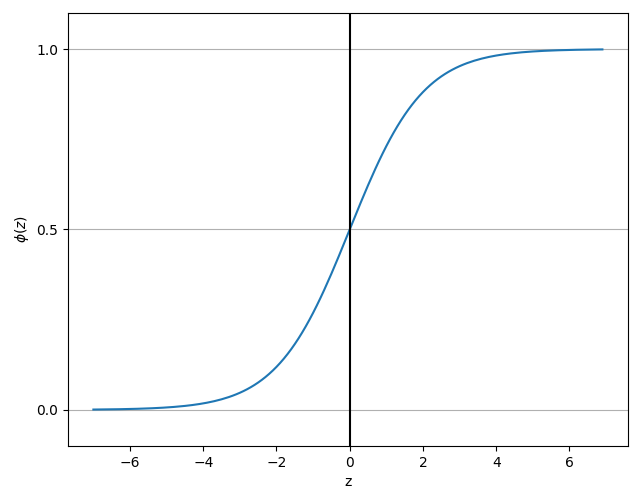

➡️ S자 형태의 (시그모이드) 곡선이 그려짐

☑️이용 분야☑️
클래스에 소속될 확률을 추정하는 것이 유용한 서비스
ex) 비 올 확률을 예측해야 하는 날씨 예보, 환자가 특정 질병을 가질 확률 예측

3.3.2 로지스틱 비용 함수의 가중치 학습

☑️로지스틱 분류 비용 그려보기☑️

def cost_1(z):
    return - np.log(sigmoid(z))


def cost_0(z):
    return - np.log(1 - sigmoid(z))

z = np.arange(-10, 10, 0.1)
phi_z = sigmoid(z)

c1 = [cost_1(x) for x in z]
plt.plot(phi_z, c1, label='J(w) if y=1')

c0 = [cost_0(x) for x in z]
plt.plot(phi_z, c0, linestyle='--', label='J(w) if y=0')

plt.ylim(0.0, 5.1)
plt.xlim([0, 1])
plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.legend(loc='best')
plt.tight_layout()
plt.show()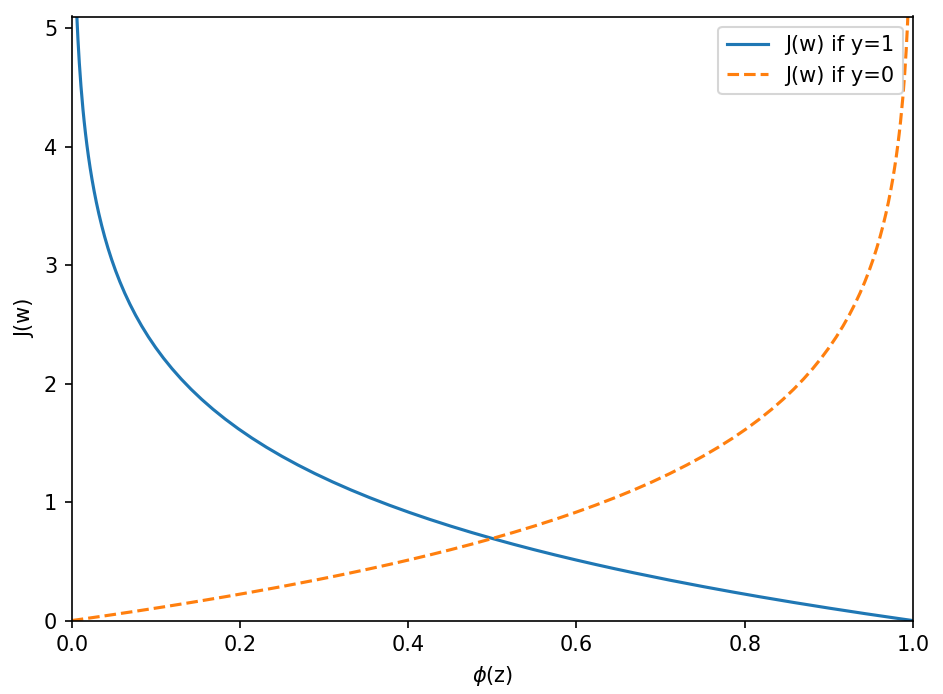

➡️ x축 : 0에서 1까지 범위의 시그모이드 활성화 값
➡️ y축 : 해당하는 로지스틱 비용
➡️ 예측이 잘못되면 비용이 무한대가 됨, 잘못된 예측에 점점 더 큰 비용을 부여

3.3.3 아달린 구현을 로지스틱 회귀 알고리즘으로 변경

• 선형 활성화 함수를 시그모이드 활성화로 바꾸기
• 임계 함수가 클래스 레이블 -1 과 1이 아닌 0과 1을 반환하도록 변경

☑️아달린 코드에 변경 사항을 반영하여 로지스틱 회귀 모델 만들기☑️

class LogisticRegressionGD(object):
    """경사 하강법을 사용한 로지스틱 회귀 분류기

    매개변수
    ------------
    eta : float
      학습률 (0.0과 1.0 사이)
    n_iter : int
      훈련 데이터셋 반복 횟수
    random_state : int
      가중치 무작위 초기화를 위한 난수 생성기 시드

    속성
    -----------
    w_ : 1d-array
      학습된 가중치
    cost_ : list
      에포크마다 누적된 로지스틱 비용 함수 값

    """
    def __init__(self, eta=0.05, n_iter=100, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

    def fit(self, X, y):
        """훈련 데이터 학습

        매개변수
        ----------
        X : {array-like}, shape = [n_samples, n_features]
          n_samples 개의 샘플과 n_features 개의 특성으로 이루어진 훈련 데이터
        y : array-like, shape = [n_samples]
          타깃값

        반환값
        -------
        self : object

        """
        rgen = np.random.RandomState(self.random_state)
        self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
        self.cost_ = []

        for i in range(self.n_iter):
            net_input = self.net_input(X)
            output = self.activation(net_input)
            errors = (y - output)
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            
            # 오차 제곱합 대신 로지스틱 비용을 계산합니다.
            cost = -y.dot(np.log(output)) - ((1 - y).dot(np.log(1 - output)))
            self.cost_.append(cost)
        return self
    
    def net_input(self, X):
        """최종 입력 계산"""
        return np.dot(X, self.w_[1:]) + self.w_[0]

    def activation(self, z):
        """로지스틱 시그모이드 활성화 계산"""
        return 1. / (1. + np.exp(-np.clip(z, -250, 250)))

    def predict(self, X):
        """단위 계단 함수를 사용하여 클래스 레이블을 반환합니다"""
        return np.where(self.net_input(X) >= 0.0, 1, 0)
        # 다음과 동일합니다.
        # return np.where(self.activation(self.net_input(X)) >= 0.5, 1, 0)

☑️이진 분류 문제로 로지스틱 회귀 구현 작동 테스트☑️

X_train_01_subset = X_train_std[(y_train == 0) | (y_train == 1)]
y_train_01_subset = y_train[(y_train == 0) | (y_train == 1)]

lrgd = LogisticRegressionGD(eta=0.05, n_iter=1000, random_state=1)
lrgd.fit(X_train_01_subset,
         y_train_01_subset)

plot_decision_regions(X=X_train_01_subset, 
                      y=y_train_01_subset,
                      classifier=lrgd)

plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')

plt.tight_layout()
# plt.savefig('images/03_05.png', dpi=300)
plt.show()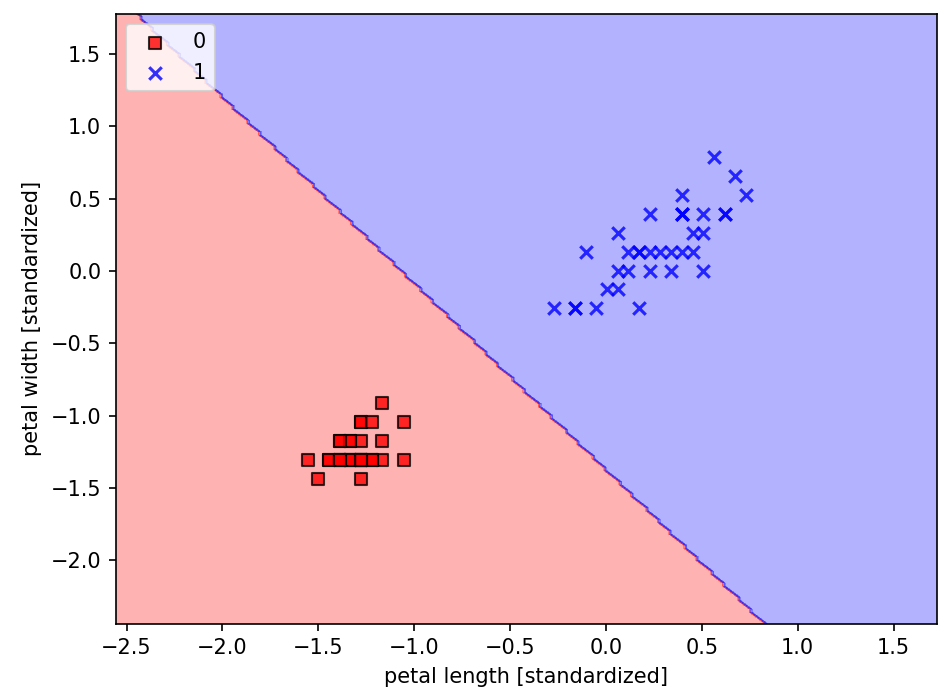

3.3.4 사이킷런을 사용하여 로지스틱 회귀 모델 훈련

☑️로지스틱 회귀 모델 훈련☑️

• 표준화 처리된 붓꽃 데이터셋의 클래스 세개를 대상으로 모델 훈련

from sklearn.linear_model import LogisticRegression

lr = LogisticRegression(C=100.0, random_state=1)
lr.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, y_combined,
                      classifier=lr, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()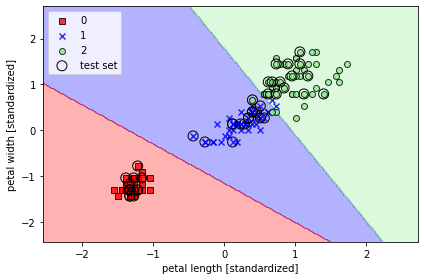

☑️훈련 샘플이 어떤 클래스에 속할 확률 계산☑️

• predict_proba 메서드 : 훈련 샘플이 어떤 클래스에 속할 확률을 계산

lr.predict_proba(X_test_std[:3, :])

➡️ 첫 번째 행 : 첫 번째 붓꽃의 클래스 소속 확률, 두 번째 행도 이와 동일
➡️ 열을 모두 더하면 1
➡️ 첫 번째 행에서 가장 큰 값은 대략 0.999 => 첫 번째 샘플이 클래스 3에 속할 확률일 99.9%
➡️ 행에서 가장 큰 값의 열이 예측 클래스 레이블이 됨 (사이킷런 사용할 때는 predict 메서드를 직접 호출하여 가능)

    lr.predict(X_text_std[:3, :])
    lr.predict(X_test_std[0, :].reshape(1, -1))

3.3.5 규제를 사용하여 과대적합 피하기

과대적합 : 모델이 훈련 데이터로는 잘 동작하지만 본 적 없는 데이터(테스트 데이터)로는 일반화가 잘 되지 않는 현상

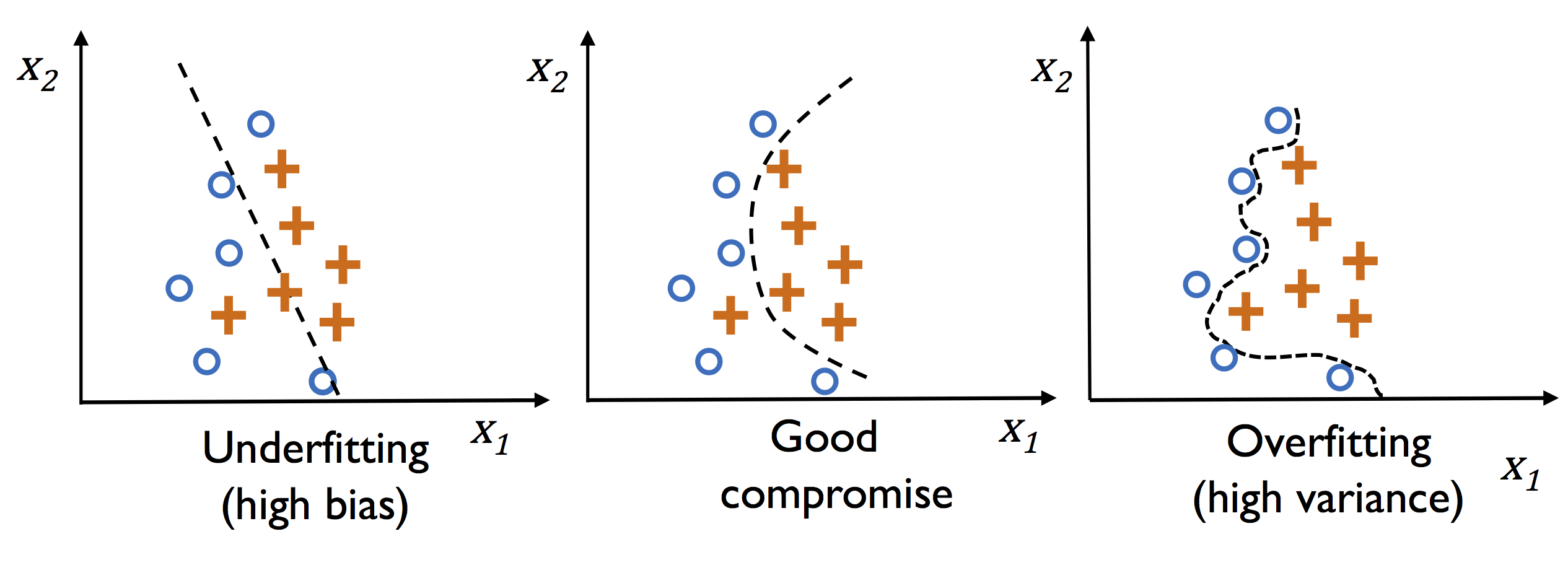
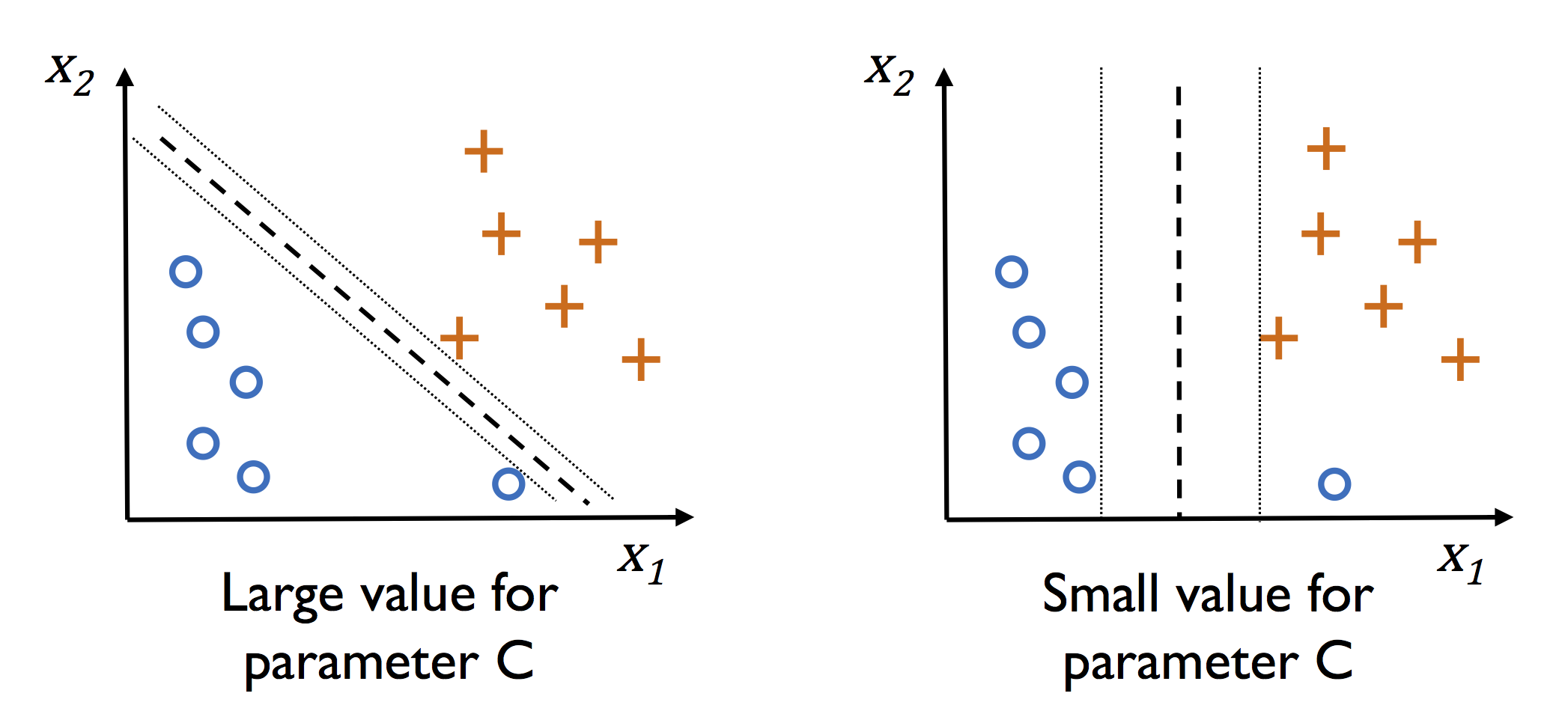
규제 : 공선성(특성 간의 높은 상관관계)을 다루거나 데이터에서 잡음을 제거하여 과대적합을 방지할 수 있는 방법,

• 과도한 파라미터(가중치) 값을 제한하기 위해 추가적인 정보(편향)을 주입 -> 모델 훈련 과정에서 가중치를 줄이는 역할
• L2 규제 -> 역 규제 파라미터 C의 값을 감소시키면 규제 강도가 증가

☑️가중치에 대한 L2규제 효과 보기☑️

weights, params = [], []
for c in np.arange(-5, 5):
    lr = LogisticRegression(C=10.**c, random_state=1, multi_class='ovr')
    lr.fit(X_train_std, y_train)
    weights.append(lr.coef_[1])
    params.append(10.**c)

weights = np.array(weights)
plt.plot(params, weights[:, 0],
         label='petal length')
plt.plot(params, weights[:, 1], linestyle='--',
         label='petal width')
plt.ylabel('weight coefficient')
plt.xlabel('C')
plt.legend(loc='upper left')
plt.xscale('log')
plt.show()

➡️ 매개변수 C가 감소하면 가중치 절댓값이 감소 -> 규제 강도 증가

3.4 서포트 벡터 머신을 사용한 최대 마진 분류

SVM의 최적화 대상 : 마진을 최대화하는 것

• 마진 : 클래스를 구분하는 초평면(결정 경계)과 이 초평면에 가장 가까운 훈련 샘플 사이의 거리
• 서포트 벡터 : 초평면에 가장 가까운 훈련 샘플
  

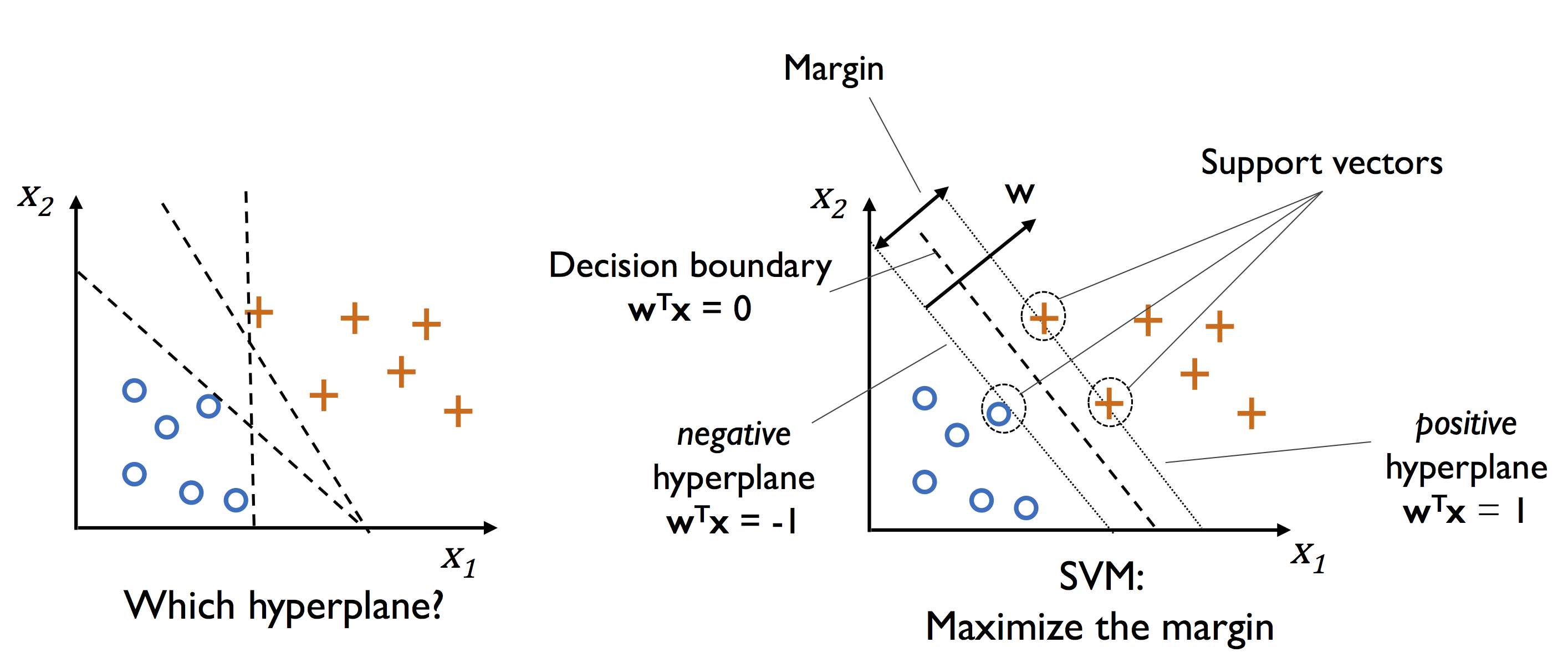
3.4.1 최대 마진

최대 마진 : 양성 샘플 쪽의 초평면과 음성 샘플 쪽의 초평면 사이의 거리를 최대화한 것

3.4.2 슬랙 변수를 사용하여 비선형 분류 문제 다루기

슬랙 변수 : 선형적으로 구분되지 않는 데이터에서 선형 제약 조건을 완화시키기 위해 더해지는 양수 값
소프트 마진 분류 : 슬랙 변수를 도입한 최대 마진 분류

☑️꽃 분류 문제에 SVM 모델을 훈련☑️

from sklearn.svm import SVC

svm = SVC(kernel='linear', C=1.0, random_state=1)
svm.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, 
                      y_combined,
                      classifier=svm, 
                      test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()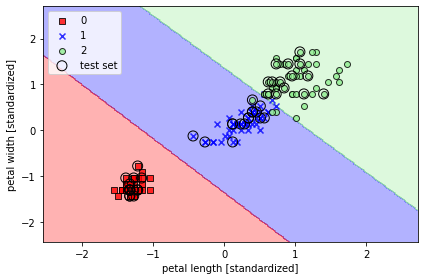

➡️ 결정 영역 세 개가 나타남

3.4.3 사이킷런의 다른 구현

데이터셋이 너무 커서 컴퓨터 메모리 용량에 맞지 않는 경우
-> SGDClassifier 클래스 제공 (partial_fit 메서드를 사용하여 온라인 학습 지원)

from sklearn.linear_model import SGDClassifier

ppn = SGDClassifier(loss='perceptron')
lr = SGDClassifier(loss='log')
svm = SGDClassifier(loss='hinge')

3.5 커널 SVM을 사용하여 비선형 문제 풀기

커널 SVM : 비선형 분류 문제를 풀기 위한 모델

3.5.1 선형적으로 구분되지 않는 데이터를 위한 커널 방법

☑️합성 데이터셋 만들기☑️

• logical_xor 함수 : XOR 형태의 간단한 데이터셋 만듦
• 샘플 100개 : 클래스 레이블 1로 할당, 나머지 샘플 100개 : 클래스 레이블 -1로 할당

import matplotlib.pyplot as plt
import numpy as np

np.random.seed(1)
X_xor = np.random.randn(200, 2)
y_xor = np.logical_xor(X_xor[:, 0] > 0,
                       X_xor[:, 1] > 0)
y_xor = np.where(y_xor, 1, -1)

plt.scatter(X_xor[y_xor == 1, 0],
            X_xor[y_xor == 1, 1],
            c='b', marker='x',
            label='1')
plt.scatter(X_xor[y_xor == -1, 0],
            X_xor[y_xor == -1, 1],
            c='r',
            marker='s',
            label='-1')

plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend(loc='best')
plt.tight_layout()
plt.show()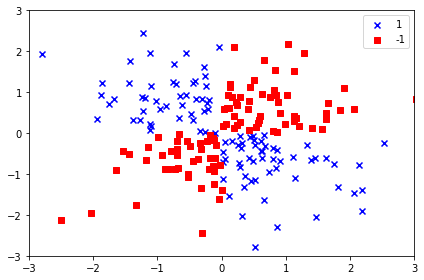

➡️ 랜덤한 잡음이 섞인 XOR 데이터셋 만들어짐


📍커널 방법의 기본 아이디어📍
매핑 함수를 사용하여 원본 특성의 비선형 조합을 선형적으로 구분되는 고차원 공간에 투영

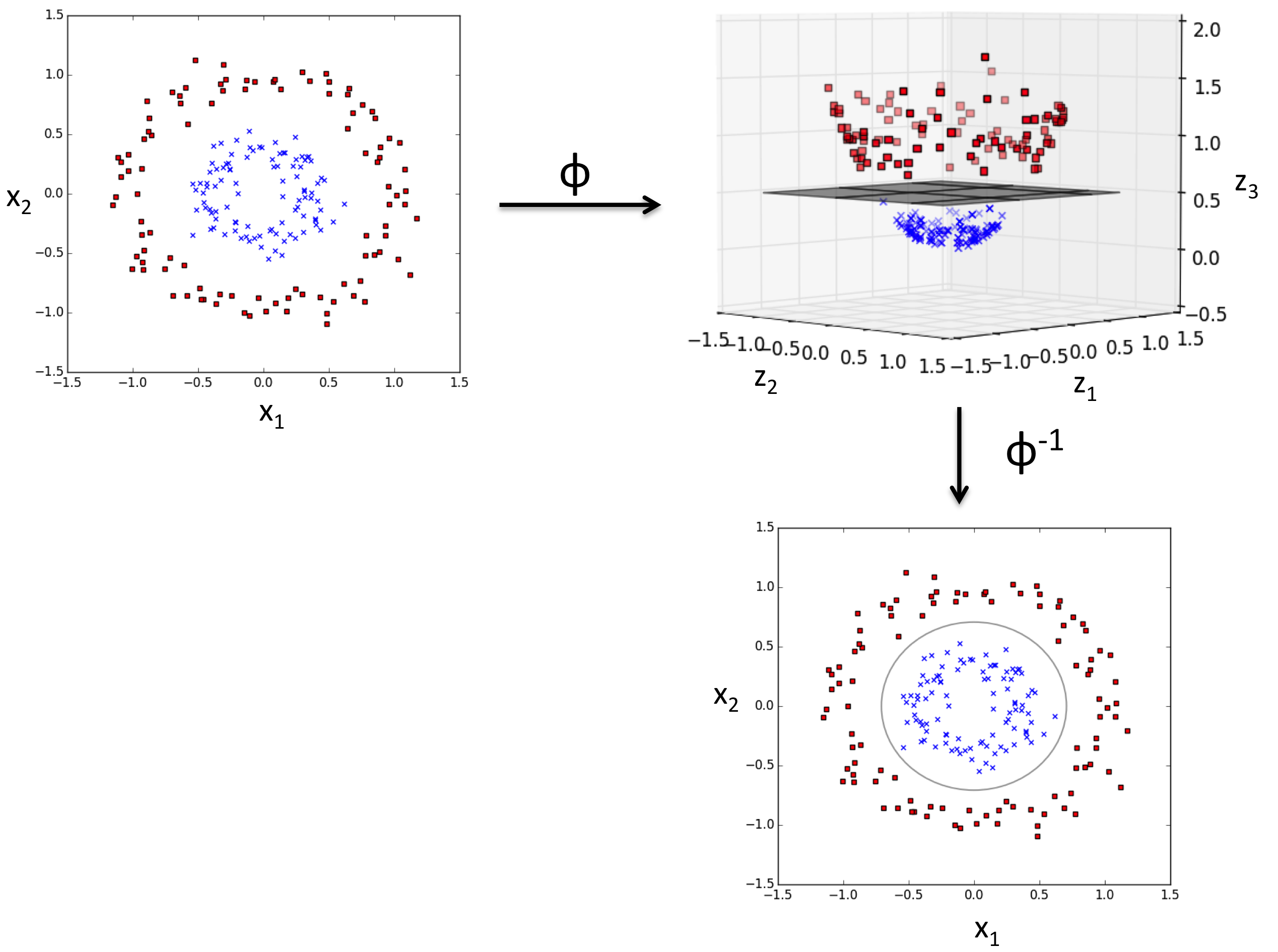
3.5.2 커널 기법을 사용하여 고차원 공간에서 분할 초평면 찾기

📍SVM으로 비선형 문제 푸는 방법📍
1) 매핑 함수를 사용하여 훈련 데이터를 고차원 특성 공간으로 변환
2) 새로운 특성 공간에서 데이터를 분류하는 선형 SVM 모델을 훈련
3) 동일한 매핑 함수를 사용하여 새로운 본 적 없는 데이터를 변환
4) 선형 SVM 모델을 사용하여 그 데이터를 분류

➡️ 계산 비용이 매우 비쌈
➡️ 커널 기법 등장


커널 : 샘플 간의 유사도 함수

• 음수 부호가 거리 측정을 유사도 점수로 바꾸는 역할
• 지수 함수로 얻게 되는 유사도 점수는 1(매우 비슷한 샘플)과 0(매우 다른 샘플)사이 범위를 가짐

☑️XOR 데이터를 구분하는 커널 SVM 훈련☑️

• SVC 클래스의 매개변수 kernel='linear'를 kernel='rbf'로 바꿈
• gamma : 가우시안 구의 크기를 제한하는 매개변수 -> 클수록 서포트 벡터의 영향이나 범위가 줄어듦

svm = SVC(kernel='rbf', random_state=1, gamma=0.10, C=10.0)
svm.fit(X_xor, y_xor)
plot_decision_regions(X_xor, y_xor,
                      classifier=svm)

plt.legend(loc='upper left')
plt.tight_layout()
plt.show()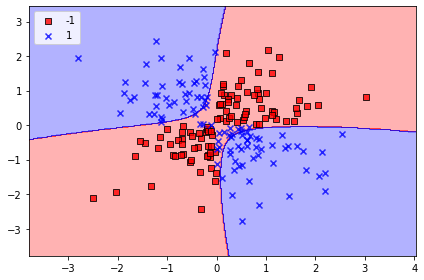

➡️ 비교적 XOR 데이터를 잘 구분함

☑️붓꽃 데이터셋에서 RBF 커널SVM 적용☑️

from sklearn.svm import SVC

svm = SVC(kernel='rbf', random_state=1, gamma=0.2, C=1.0)
svm.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, y_combined,
                      classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

➡️ gamma 값을 비교적 작게 했기 때문에 결정 경계가 부드러움

☑️ gamma 값을 크게 하고 결정 경계 보기☑️

svm = SVC(kernel='rbf', random_state=1, gamma=100.0, C=1.0)
svm.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, y_combined, 
                      classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()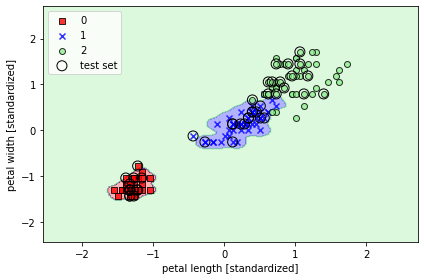

➡️ 훈련 데이터에서는 잘 맞지만 테스트 데이터에서는 일반화 오차가 높을 것
➡️ gamma 매개변수가 과대적합 또는 분산을 조절하는 중요한 역할
➡️ SVM 모델에 규제를 가할 때는 gamma와 C 매개변수를 동시에 조절하는 것이 좋음

3.6 결정 트리 학습

결정 트리 : 훈련 데이터에 있는 특성을 기반으로 샘플의 클래스 레이블을 추정할 수 있는 일련의 질문을 학습

• 트리의 루트에서 시작해서 정보 이득이 최대가 되는 특성으로 데이터를 나눔
• 반복 과정을 통해 리프 노드가 순수해질 때까지 모든 자식 노드에서 이 분할 작업을 반복 -> 과대적합될 가능성 -> 트리의 최대 깊이를 제한하여 가지치기

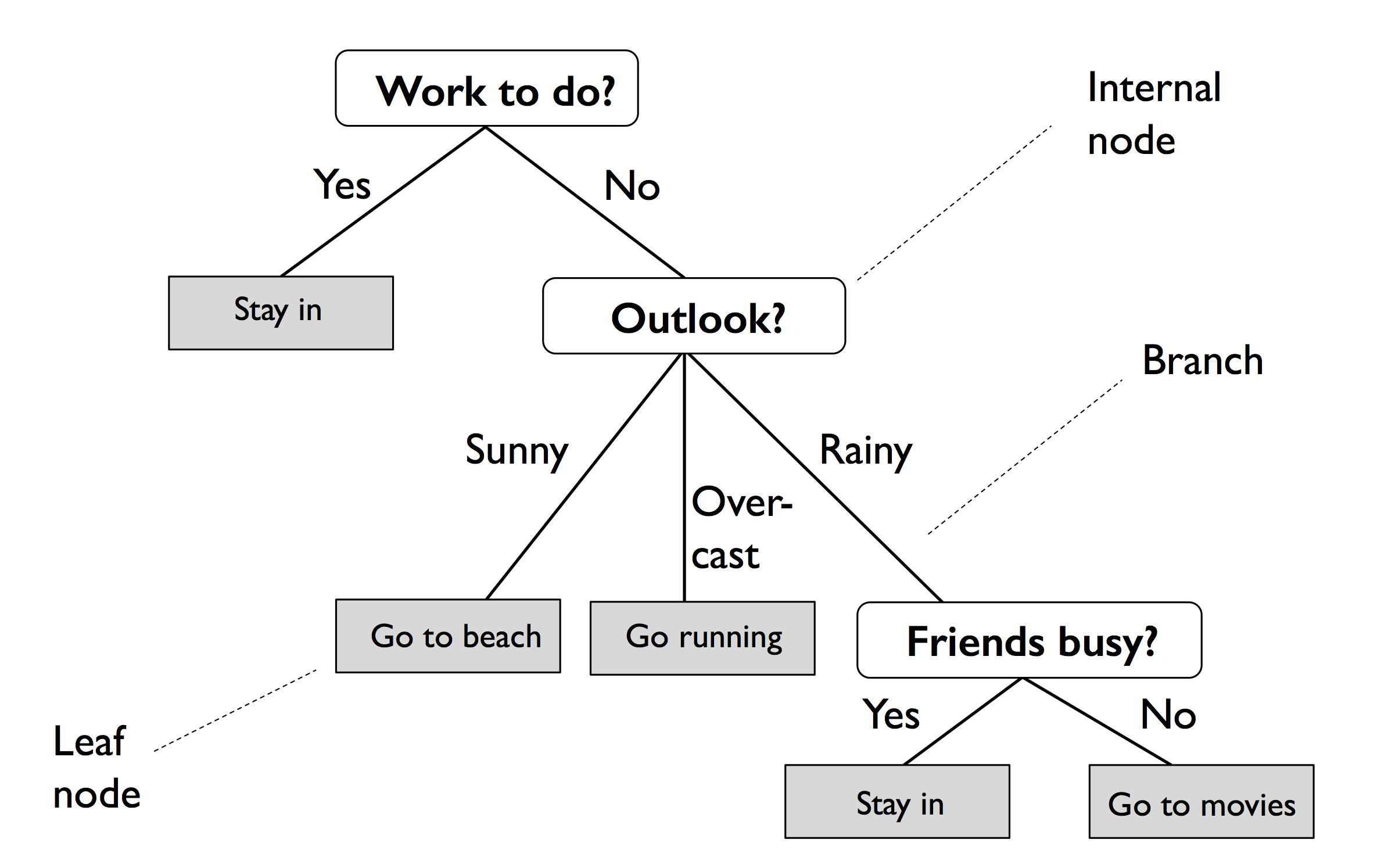
3.6.1 정보 이득 최대화: 자원을 최대로 활용

가장 정보가 풍부한 특성으로 노드를 나누기 위해 -> 트리 알고리즘으로 최적화할 목적 함수를 정의

목적 함수 - 각 분할에서 정보 이득을 최대화함

• 정보 이득 : 부모 노드의 불순도와 자식 노드의 불순도 합의 차이 (자식 노드의 불순도가 낮을 수록 정보 이득이 커짐)

이진 결정 트리 사용 : 구현 간단하게 하고 탐색 공간 줄이기 위해

📍이진 결정 트리에 사용되는 불순도 지표 또는 분할 조건📍
1) 지니 불순도 : 클래스가 완벽하게 섞여 있을 때 최대가 됨
2) 엔트로피 : 클래스 분포가 균등하면 엔트로피 최대가 됨
3) 분류 오차 : 두 클래스가 같은 비율일 때 최대(0.5)가 됨

☑️불순도 기준 비교 위한 클래스 1의 확률 범위 [0, 1]에 대한 불순도 인덱스 그려보기☑️

• 스케일 조정된 엔트로피(엔트로피 / 2)를 추가 : 지니 불순도가 엔트로피와 분류 오차의 중간임을 관찰

import matplotlib.pyplot as plt
import numpy as np


def gini(p):
    return p * (1 - p) + (1 - p) * (1 - (1 - p))


def entropy(p):
    return - p * np.log2(p) - (1 - p) * np.log2((1 - p))


def error(p):
    return 1 - np.max([p, 1 - p])

x = np.arange(0.0, 1.0, 0.01)

ent = [entropy(p) if p != 0 else None for p in x]
sc_ent = [e * 0.5 if e else None for e in ent]
err = [error(i) for i in x]

fig = plt.figure()
ax = plt.subplot(111)
for i, lab, ls, c, in zip([ent, sc_ent, gini(x), err], 
                          ['Entropy', 'Entropy (scaled)', 
                           'Gini impurity', 'Misclassification error'],
                          ['-', '-', '--', '-.'],
                          ['black', 'lightgray', 'red', 'green', 'cyan']):
    line = ax.plot(x, i, label=lab, linestyle=ls, lw=2, color=c)

ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.15),
          ncol=5, fancybox=True, shadow=False)

ax.axhline(y=0.5, linewidth=1, color='k', linestyle='--')
ax.axhline(y=1.0, linewidth=1, color='k', linestyle='--')
plt.ylim([0, 1.1])
plt.xlabel('p(i=1)')
plt.ylabel('impurity index')
plt.show()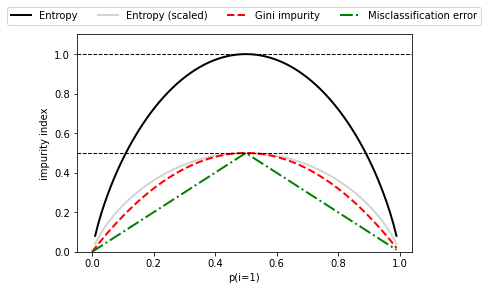

3.6.2 결정 트리 만들기

결정 트리 - 특성 공간을 사각 격자로 나누기 때문에 복잡한 결정 경계 만들 수 ⭕

☑️최대 깊이가 4인 결정 트리를 훈련☑️

from sklearn.tree import DecisionTreeClassifier

tree_model = DecisionTreeClassifier(criterion='gini', 
                                    max_depth=4, 
                                    random_state=1)
tree_model.fit(X_train, y_train)

X_combined = np.vstack((X_train, X_test))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X_combined, y_combined, 
                      classifier=tree_model,
                      test_idx=range(105, 150))

plt.xlabel('petal length [cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()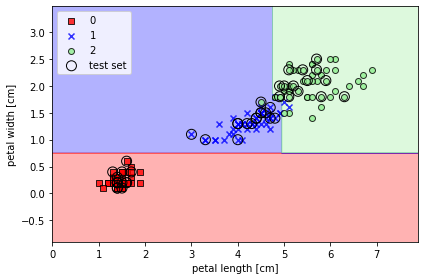

➡️ 축에 나란히 놓인 전형적인 결정 트리의 결정 경계 얻음

☑️사이킷런으로 훈련된 결정 트리 모델 시각화☑️

from sklearn import tree

tree.plot_tree(tree_model)
plt.show()

☑️PyDotPlus 설치☑️

pip3 install pydotplus
conda install pydotplus

☑️로컬 디렉터리에 PNG 포맷의 결정 트리 이미지 생성☑️

• out_file=None : tree.dot 중간 파일을 디스크에 만들지 않고 dot 데이터를 바로 dot_data 변수에 할당
• filled : 색 추가 옵션
• rounded : 상자 모서리의 라운드 처리 옵션
• class_naes : 각 노드에 다수 클래스 레이블 이름 표시 옵션
• feature_names : 분할 기준에 특성 이름 표시에 관한 옵션

from pydotplus import graph_from_dot_data
from sklearn.tree import export_graphviz

dot_data = export_graphviz(tree_model,
                           filled=True, 
                           rounded=True,
                           class_names=['Setosa', 
                                        'Versicolor',
                                        'Virginica'],
                           feature_names=['petal length', 
                                          'petal width'],
                           out_file=None) 
graph = graph_from_dot_data(dot_data) 
graph.write_png('tree.png')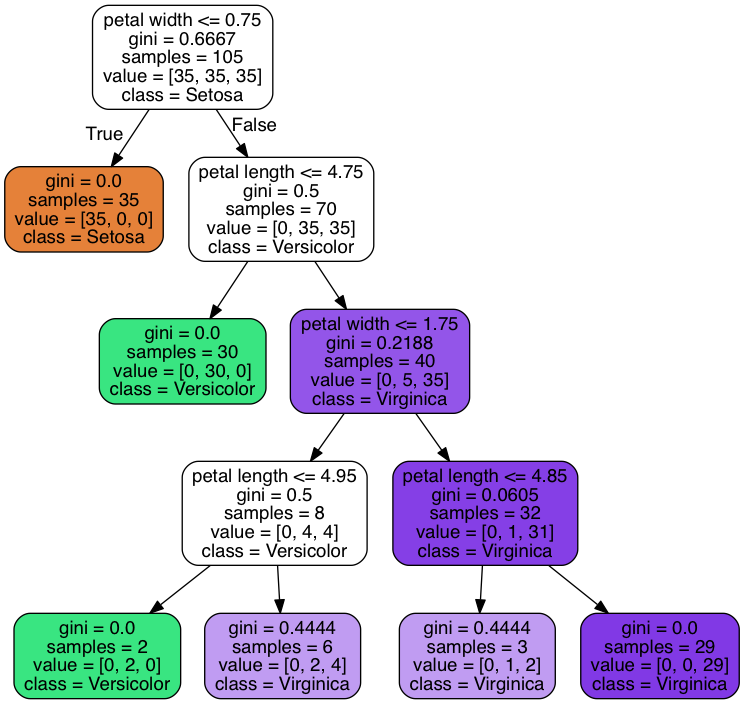 

➡️ 루트 노드에서 105개의 샘플로 시작
➡️ 꽃잎 너비 기준 0.75 센터미터 이하를 사용해서 35개와 70개의 샘플을 가진 두 개의 자식 노드로 분할
➡️ 첫 번째 분할 - 왼쪽 자식 노드는 Iris-setosa 클래스의 샘플만 가진 순수 노드
➡️ 오른쪽에서 분할이 더 일어나 Iris-veriscolor와 Iris-virginica 클래스의 샘플 구분

3.6.3 랜덤 포레스트로 여러 개의 결정 트리 연결

앙상블 - 뛰어난 분류 성능과 과대적합에 안정적 -> 머신 러닝 애플리케이션에서 큰 인기를 누림
랜덤 포레스트 : 결정 트리의 앙상블

• 아이디어 : 여러 개의 (깊은) 결정 트리를 평균 내는 것
• 단계
  • n개의 랜덤한 부트스트랩 샘플을 뽑음(훈련 데이터셋에서 중복을 허용하면서 랜덤하게 n개의 샘플을 선택)
  • 부트 스트램 샘플에서 결정 트리를 학습
    • 중복을 허용하지 않고 랜덤하게 d개의 특성을 선택
    • 정보 이득과 같은 목적 함수를 기준으로 최선의 분할을 만드는 특성을 사용해서 노드를 분할
  • 단계 1~2를 k번 반복
  • 각 트리의 예측을 모아 다수결 투표로 클래스 레이블을 할당
• 장점 : 결정 트리만큼 해석이 쉽지는 않지만 하이퍼파라미터 튜닝에 많은 노력을 기울이지 않아도 됨, 가지치기할 필요가 ❌

☑️사이킷런을 이용하여 랜덤 포레스트 분류기 생성☑️

• n_estimators=25 : 25개의 결정 트리를 사용하여 랜덤 포레스트 훈련
• n_jobs=2 : 컴퓨터의 멀티 코어 2개를 사용해서 모델 훈련을 병렬화

from sklearn.ensemble import RandomForestClassifier

forest = RandomForestClassifier(criterion='gini',
                                n_estimators=25, 
                                random_state=1,
                                n_jobs=2)
forest.fit(X_train, y_train)

plot_decision_regions(X_combined, y_combined, 
                      classifier=forest, test_idx=range(105, 150))

plt.xlabel('petal length [cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()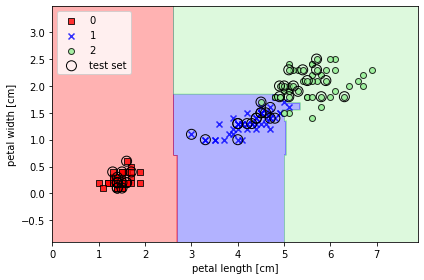

➡️ 랜덤 포레스트의 트리 앙상블이 만든 결정 영역

3.7 k-최근접 이웃: 게으른 학습 알고리즘

KNN : 게으른 학습기 -> 훈련 데이터에서 판별 함수를 학습하는 대신 훈련 데이터셋을 메모리에 저장

• 단계
  • 숫자 k와 거리 측정 기준을 선택
  • 분류하려는 샘플에서 k개의 최근접 이웃을 찾음
  • 다수결 투표를 통해 클래스 레이블을 할당
• 장점 : 새로운 훈련 데이터에 즉시 적응할 수 있는 점
• 단점 : 계산 복잡도, 훈련 단계가 없기 때문에 훈련 샘플을 버릴 수 ❌

☑️유클라디안 거리 측정 방식을 사용한 사이킷런의 KNN 모델 만들기☑️

• p 매개변수 : 2로 지정하면 유클리디안 거리, 1로 지정하면 맨해튼 거리

from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier(n_neighbors=5, 
                           p=2, 
                           metric='minkowski')
knn.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, y_combined, 
                      classifier=knn, test_idx=range(105, 150))

plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()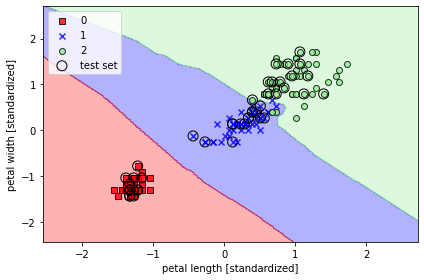

➡️ 5개의 이웃을 지정 -> 비교적 부드러운 결정 경계 얻음
➡️ 적절한 k를 선택하는 것이 올바른 균형을 잡기 위해 중요