Sort (2)

Heap Sort

Heap이라는 우선순위가 적용되어 저장되는 자료구조를 활용하여 정렬하는 방식

//오름차순 정렬 메서드
int PriComp(int n1, int n2) {
    return n2 - n1;
}

//Heap을 활용한 정렬
int HeapSort(int arr[], int n, PriorityComp pc) {
    Heap heap;
    int i;

    HeapInit(&heap, pc);

    for(i = 0; i < n; i++) {
        HInsert(&heap, arr[i]);
    }

    for(i = 0; i < n; i++) {
        arr[i] = HDelete(&heap);
    }
  
  return 0;
}

Heap에 데이터를 Insert하는 것 만으로도 정렬이 이루어 진다.

HeapInit시 원하는 정렬 기준(PriComp)를 설정하여 정렬을 한다.

Heap의 삭제 로직을 순차적으로 배열(arr) 에 대입하여 정렬된 배열을 얻는다.

HeapSort의 핵심은 사실, Heap의 동작과정을 이해하는 것이다.

성능 평가

(정렬 데이터의 크기) X (힙의 삽입연산 + 삭제연산)

힙 삽입 & 삭제 연산의 BigO => $O(log_2n)$

$n$개의 데이터를 정렬한다면, $n * (2log_2n)$의 성능을 보여주고,

BigO로 표현하면 $O(n\log_2n)$이다.

MergeSort

핵심 아이디어는, 정렬할 데이터들을 모두 분할하고 다시 합치는 과정에서 정렬한다는 것이다.

ex) [3, 2, 4, 1] 을 병합정렬을 한다면,

1. [3], [2], [4], [1]로 분할
2. 병합 & 정렬 -> [2, 3], [1, 4]
3. 재귀적으로 반복

MergeSort()

int MergeSort(int arr[], int left, int right) {
    int mid;

    if(left < right) {
        mid = (left + right) / 2;

        MergeSort(arr, left, mid);
        MergeSort(arr, mid + 1, right);
      //재귀를 통해 분할이 되지 않을 때까지 분할

        MergeTwoArea(arr, left, mid, right); //병합하는 과정
    }
  
  	return 0;
}

MergeTwoArea()

int MergeTwoArea(int arr[], int left, int mid, int right) {
    int fIdx = left;
    int rIdx = mid + 1;
    int i;

    int *sortArr = (int *)malloc(sizeof(int) * (right + 1)); //병합될 배열 할당
    int sIdx = left;

  //오름차순인 경우 정렬하여 담기
  //병합할 두 영역(왼쪽, 오른쪽)은 이미 정렬되어있음
    while(fIdx <= mid && rIdx <= right) {
        if(arr[fIdx] <= arr[rIdx]) //양쪽 영역의 데이터를 비교하여 새로운 배열에 정렬기준으로 저장
            sortArr[sIdx] = arr[fIdx++];
        else
            sortArr[sIdx] = arr[rIdx++];

        sIdx++;
    }

    if(fIdx > mid) { //왼쪽이 다 채워진 경우
        for(i = rIdx; i <= right; i++, sIdx++)
            sortArr[sIdx] = arr[i];
    }
    else { //오른쪽이 다 채워진 경우
        for(i = fIdx; i <= mid; i++, sIdx++)
            sortArr[sIdx] = arr[i];
    }

  //기존 배열에 정렬 결과 반영
    for(i = left; i <= right; i++) {
        arr[i] = sortArr[i];
    }

    free(sortArr); //임시 배열의 메모리 해제
    return 0;
}

성능평가

Size가 n인 배열의 정렬인 경우

분할과정은 정렬 크기를 2로 계속해서 나누며 수행한다. => $log_2n$

병합과정을 보면, 새로운 배열을 할당하고 이에 데이터를 넣을 때 n만큼 (최대) 비교연산과 실제 배열에 옮기는 연산 $n$만큼 => $2n$

BigO => $O(nlog_2n)$

참고 이미지 (from Khan Academy)

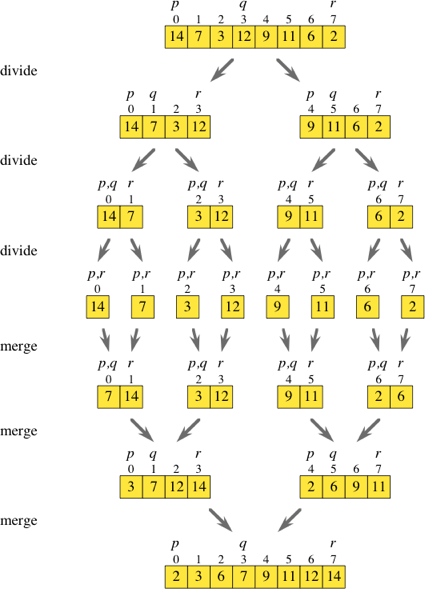
QuickSort

병합정렬과 비슷하게 영역을 나누어 재귀적으로 해결하는 아이디어를 가진다.

정렬하려는 배열에 5가지 point가 필요하다

1. pivot : 중심축
2. left : 정렬 대상의 가장 왼쪽
3. right : 정렬 대상의 가장 오른쪽
4. low : 피벗을 제외한 가장 왼쪽을 가리키는 점
5. high : 피벗을 제외한 가장 오른쪽 가리키는 점

동작 과정

1. 정렬할 배열 내에 임이의 원소 Pivot을 정한다

2. low는 증가, high는 감소하면서 서로 비교한다. 만약 left > right인 경우 교환한다. (오름차순인 경우)

3. low와 high가 이동하다 서로 위치가 역전(교차)되면, (2)과정을 멈추고 high와 피벗의 위치를 교환한다

   -> 위 과정으로 pivot은 해당 배열에서 본인 자리로 들어가게 된다.

4. 피벗 기준 왼쪽 배열과 오른쪽 배열로 나누어 재귀적으로 퀵 정렬을 수행한다.

void Swap(int arr[], int idx1, int idx2) {
    int temp = arr[idx1];
    arr[idx1] = arr[idx2];
    arr[idx2] = temp;
}

int Partition(int arr[], int left, int right) {
    int pivot = arr[left];
    int low = left + 1;
    int high = right;

    while(low <= high) { //교차하기 전까지
        if(arr[low] <= pivot && low <= right)
            low++;

        if(arr[high] > pivot && high >= left + 1)
            high--;

        if(low <= high)
            Swap(arr, low, high); //우선순위에 맞게 low와 high인덱스 교환
    }

    Swap(arr, left, high);

    return high; //정렬된 피봇 반환
}

void QuickSort(int arr[], int left, int right) {
    if(left <= right) {
        int pivot = Partition(arr, left, right);
        QuickSort(arr, left, pivot - 1); //피벗 기준 왼쪽 영역
        QuickSort(arr, pivot + 1, right); //피벗 기준 오른쪽 영역
    }
}

성능 평가

Quick이라는 수식어와 달리 최악의 경우 BigO는 $n^2$이다.

최악의 경우 : 1, 2, 3, 4, 5

n만큼 재귀하며, n번 정렬이 이루어 진다

QuickSort가 주로 사용되는 이유는 평균적으로 $n(log_2n)$을 따르기 때문이다.

이러한 편차는 처음 피벗설정에 달려 있다.
만약 초기 설정한 피벗이 중앙값에 가깝다면, $log_2n$ 번 만큼 재귀할 것이다.

• 최악 : 이미 정렬되어있는 리스트에서 매번 첫 번째 원소를 피벗으로 고를 때. => $O(n^2)$
• 최적 : 매번 자료의 중위값(median)을 피벗으로 고를 때. => $O(n log_2 n)$

무작위한 배열을 정렬한다 했을때, 중앙값을 고를 확률이 가장 높지 않은가. 반대로, 중앙값을 찾아 피벗으로 설정한다면 항상 최적의 성능을 얻을 수 있다.