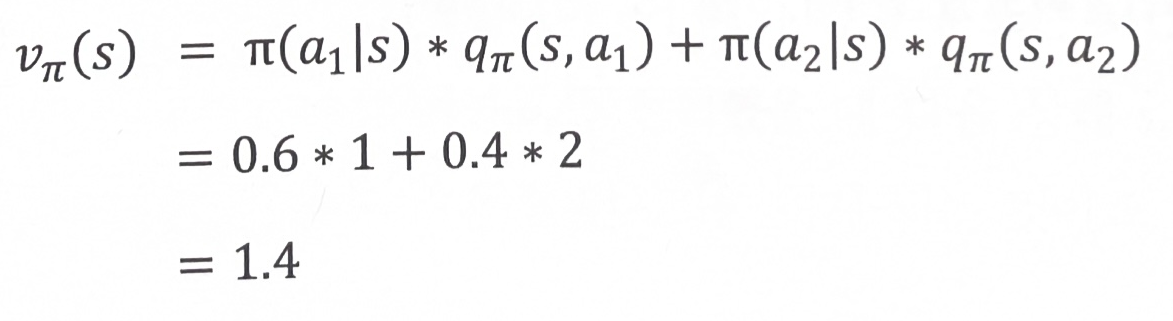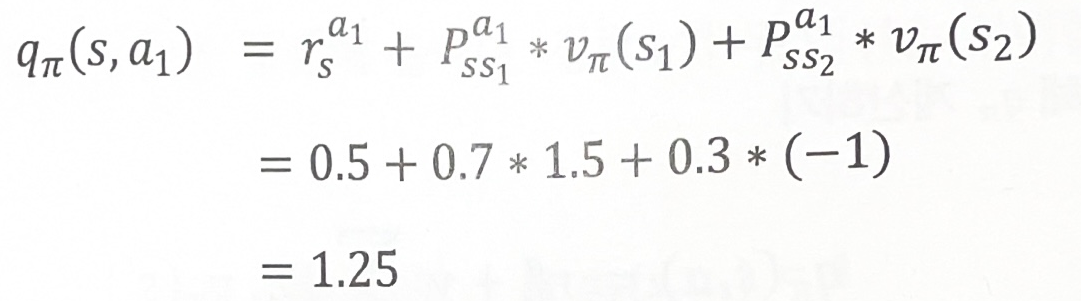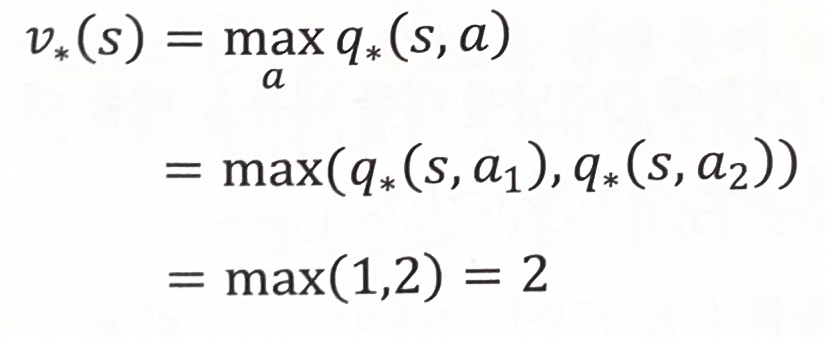벨만 방정식
- 주어진 상태의 가치를 구하는 방법
- 현재 시점 t와 다음 시점 t+1의 재귀적 관계를 이용
1. 벨만 기대 방정식

- 0단계
vπ(st)=E[rt+1+γvπ(st+1)] vπ(st)=E[Gt]
- s의 가치 = 기댓값 연산자[리턴] = 리턴의 기댓값
- 1단계
vπ(st)=a∈A∑π(a∣s)qπ(s,a)
- s의 가치 = 모든 액션의 합{(s에서 a를 실행할 확률)*(s에서 a를 실행하는 것의 가치)}
- [주어진 조건]
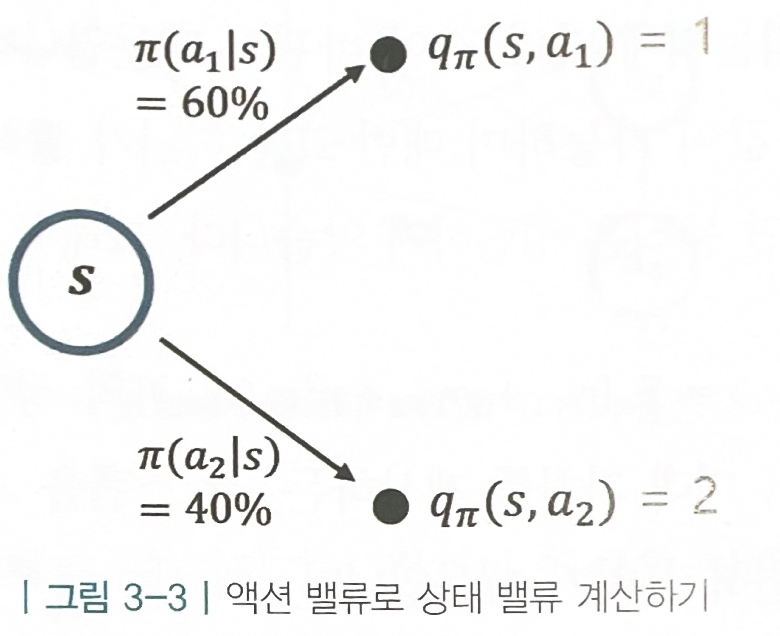
- 식 대입 계산
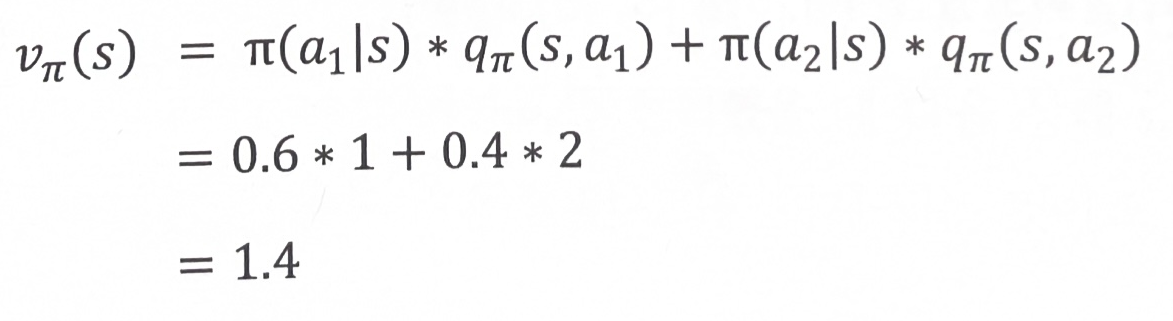
qπ(s,a)=rsa+γs′∈S∑pss′avπ(s′)
- s에서 a를 실행하는 것의 가치 =
즉시 얻는 보상 + 모든 상태의 합{(s에서 a를 실행하면 s’에 도착학 확률)*(s’의 가치)}
- 주어진 조건

- 식 대입 계산
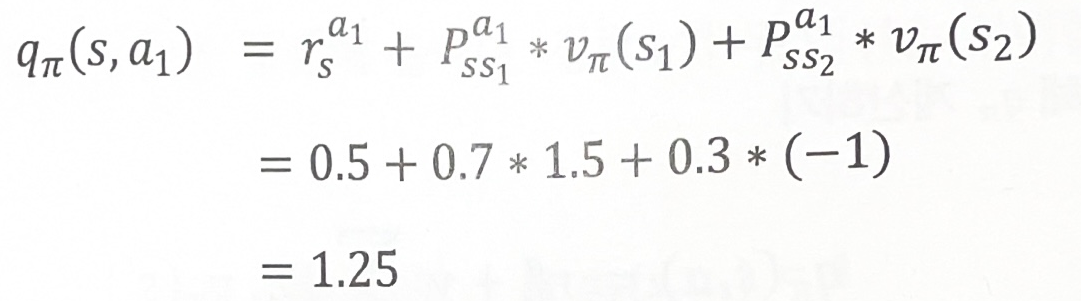
- 2단계
- 각각 식 대입
vπ(st)=a∈A∑π(a∣s)(rsa+γs′∈S∑pss′avπ(s′)) qπ(s,a)=rsa+γs′∈S∑pss′aa∈A∑π(a′∣s′)qπ(s′,a′)
- 2단계 식을 계산하기 위해 알아야 할 것
- 보상 함수 r : 각 상태에서 액션을 선택하면 얻는 보상
- 전이 확률 P : 각 상태에서 액션을 선택하면 다음 상태가 어디가 될 지에 관한 확률 분포
2. 벨만 최적 방정식
- 최적의 가치(가치 함수의 결과가 가장 큰)를 찾는 일을 할 때 사용
v∗(s)=maxπvπ(s)
q∗(s,a)=maxπqπ(s,a)
- MDP가 주어졌을 때,
그 MDP 안에 존재하는 모든 π(정책)들 중에서 가장 좋은(vπ(s)의 최고 가치) π를 선택해 계산한 가치가 곧 최적 가치 v*(s)
- 여러 정책들 중에vπ1(s0),vπ2(s0),vπ3(s0),...vπn(s0)
- 만약 최적 정책을 찾았다면 (만약 π238 가장 값이 크다면)
v∗(s0)=vπ238(s0)
- 벨만 최적 방정식

- 0단계
v∗(st)=maxaE[rt+1+γv∗(st+1)]
- 정책 π 대신 max 함수 사용
- s의 가치 = 최댓값 (기댓값 연산자[리턴]) = 리턴의 기댓값의 최댓값
- 전이 확률에 의해 다양한 s’ 나올 수 있어서 기댓값 연산자 필요
q∗(st,at)=E[rt+1+γmaxa′q∗(st+1,a′)]
- 1단계
v∗(s)=maxaq∗(s,a)
- s의 최적 가치 = s에서 선택할 수 있는 액션들 중에 가장 높은 액션의 가치
- [주어진 조건]
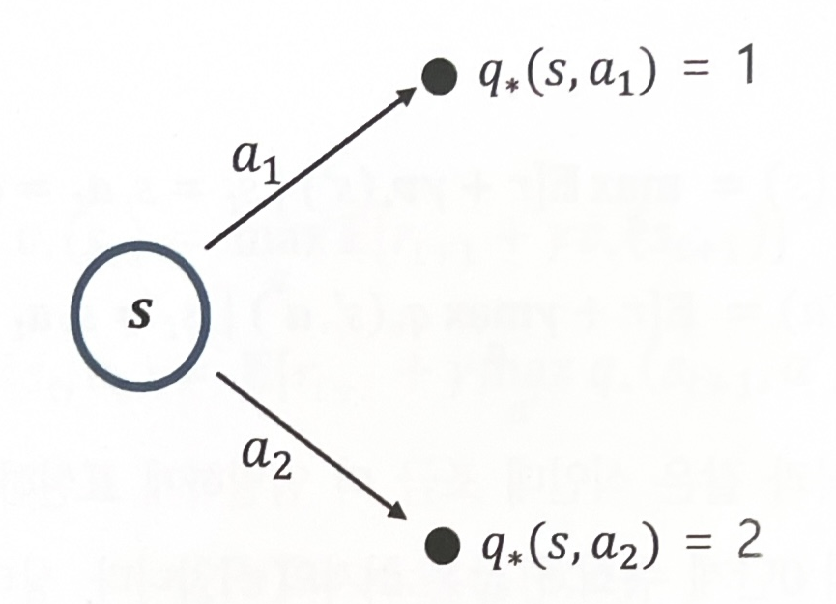
- [식대입 계산]
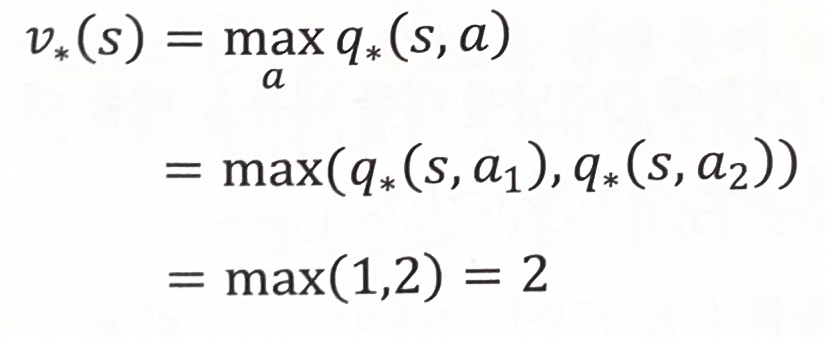
q∗(s,a)=rsa+γs′∈S∑Pss′av∗(s′)