[알고리즘] Backtracking

최원석·2024년 12월 17일

알고리즘

💫Backtracking

모든 경우의 수를 전부 고려하는 알고리즘. 상태공간을 트리로 나타낼 수 있을 때 적합한 방식이다.

어떤 노드에서 유망성을 점검한 후, 유망하지 않다고 판정되면 그 노드의 부모노드로 돌아가서(”backtrack”) 다음 후손노드에 대한 검색을 계속 진행하는 과정이다.

Promising : 해답이 나올 가능성이 있다. → 유망하다.

non - Promising : 해답이 나올 가능성이 없다.→ 유망하지 않다.

📁 backtrack

일반적인 되추적 알고리즘

void checknode (node v) {
	  node u;
   if (promising(v))
      if (there is a solution at v)
         write the solution;
      else
      	for (each child u of v)
				   checknode(u);
}

개선된 되추적 알고리즘

void expand (node v) {
		node u;
		for (each child u of v)
				if (promising(u))
				if (there is a solution at u)
						write the solution;
				else
						expand(u);
}

💫 Depth - First Search ( 깊이우선검색 )

뿌리 노드 ( root )가 되는 노드( node )를 먼저 방문한 뒤, 그 노드의 모든 후손노드들을 차례로 방문 / 왼 → 오

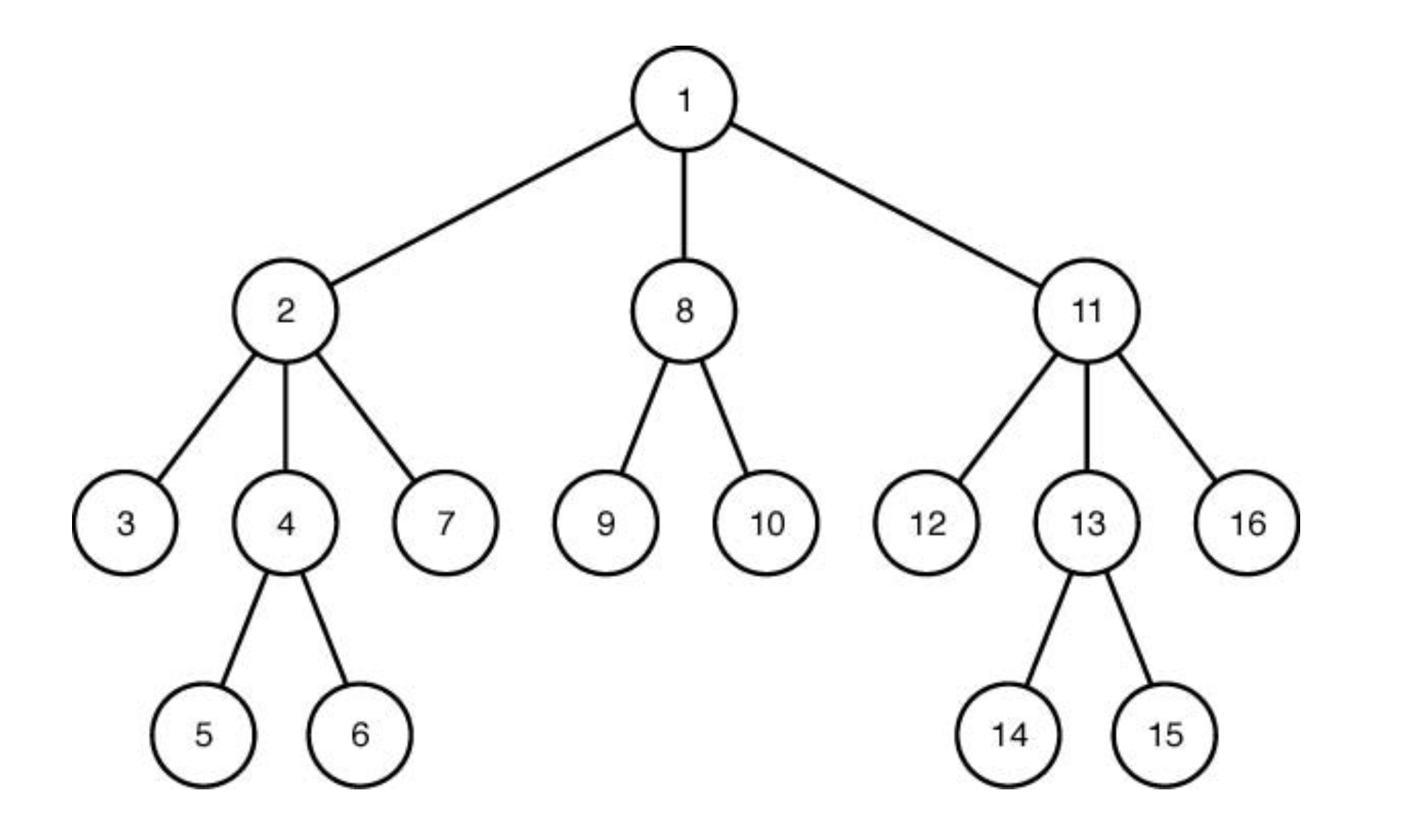
💫 4-Queen Problem

4개의(n개도 가능) Queen을 서로 상대방을 위협하지 않도록
상대방의 Queen을 위협하지 않기 위해 같은 행이나, 같은 열, 대각선 상에 위치하지 않아야한다. ( 엥 근데 체스는 1:1 게임인데… ?)

문제를 어떻게 접근할까..?

❗️ 무작정 알고리즘
각 Queen을 각각 다른 행에 할당한 후에, 어떤 열에 위치하면 해답은 얻을 수 있는지를 차례대로 점검해 보면 된다.
이때, 각 Queen은 4개의 열 중에서 한 열에 위치할 수 있기 때문에, 해답을 얻기 위해서 점검해 보아야 하는 모든 경우의 수는 4 x 4 x 4 x 4 = 256가지가 된다.

📁 4-Queens 문제의 상태공간 트리

❓ 상태공간 트리

뿌리 노드에서 잎노드 까지의 경로가 해답 후보가 되는 것.
→ 깊이우선검색을 하여 그 해답후보 중에서 해답을 찾을 수 있다.

상태공간트리에서 깊이우선검색을 하면 해답을 찾을 수 있지만 모든 후손노드들을 방문애햐 하므로 굉장히 비효율적이다.

📁 의사 코드

행렬을 체스판이라고 생각!

void queens (index i) {
 index j;
 	   if (promising (i))
     	  if (i == n)  cout << col[1] through col[n];
     else
     	  for (j=1; j<=n; j++) {
  	    	col[i+1] = j;
  	    	queens(i+1);
		  }
}

 bool promising (index i) {
   index k;
   bool switch;
   
   k = 1;
   switch = TRUE;
   while (k<i && switch) {
      if (col[i]==col[k] || abs(col[i]–col[k])==abs(i-k))
         switch = FALSE;
	  k++ 
   }
   return switch;
}

N-Queens에서 코드 분석

같은 열인 경우 non promising

If (col(i) == col(k)) nonpromising;

대각선인 경우 non promising

If (abs(col(i) - col(k)) == abs(i - k)) nonpromising;

📁 n - Queens Problem 분석 - 1

상태공간트리 전체에 있는 노드의 수를 구함으로서, 가지 친 상태공간의 노드의 개수의 상한을 구한다.

깊이가 i인 노드의 개수는 $n^i$ 개 이고, 이 트리의 깊이는 n이므로, 노드의 총 개수의 상한은 아래 식과 같다.

1 + n + n^2 + n^3 + \cdots + n^n = \frac{n^{n+1} - 1}{n - 1}

열심히 적었지만…. 이 분석은 별 가지가 없다. ㅠ

왜냐, 되추적함으로서 점검하는 노드 수를 얼마나 줄였는지 상한값을 구해서는 전혀 알 수 없기 때문이다.

📁 n - Queens Problem 분석 - 2

유망한 노드만 카운트해 상한을 구한다.

→ 어떤 두 개의 Queen이 같은 열에 위치할 수 없다는 사실을 이용하면 된다.

1 + n + n(n-1) + n(n-1)(n-2) + \cdots + n!

하지만… 2번 또한 그렇게 가치있는 분석은 아니다.

위 2가지 분석은 알고리즘의 복잡도를 정확히 얘기해주지 못하고 있다.

대각선을 점검하는 경우를 고려하지 않음 → 실제 유망한 노드의 수는 훨씬 더 작을 수 있다.
유망하지 않은 노드의 일부만 포함하고 있다. → 유망하지 않은 노드는 훨씬 더 많을 수 있다.

💫 Monte Carlo Algorithm

어떤 입력이 주어졌을 때 점검하게 되는 상태공간 트리의 “전형적인” 경로를 무작위로 생성하여 그 경로 상에 있는 노드의 수를 센다. → 과정을 반복하여 나오는 결과의 평균치를 추정치로 한다.

이 기법을 적용하기 위한 필수 조건

상태공간트리에서 같은 level에 있는 모든 노드에서는 같은 유망함수를 사용해야함
상태 공간트리에서 같른 수준에 있는 모든 노드들은 같은 수의 자식노드들을 가지고 있어야 한다.

📁 백트랙킹 알고리즘 수행시간 추정 방법

뿌리노드의 유망한 자식노드의 개수를 $m_0$ 이라고 한다.
상태공간트리의 수준 1에서 유망한 노드 하나를 무작위로 정하고, 그 노드의 유망한 자식노드의 개수를 $m_1$ 이라고 한다.
위에서 정한 노드의 유망한 노드 하나를 다시 무작위로 정하고, 그 노드의 유망한 자식노드의 개수를 $m_2$ 라고 한다.
더 이상 유망한 자식노드가 없을 때까지 이 과정을 반복한다.

1 + t_0 + m_0 t_1 + m_0 m_1 t_2 + \cdots + m_0 m_1 \cdots m_{i-1} t_i + \cdots

$m_i$ 는 수준 i에 있는 노드의 유망한 지식노드의 개수이 평균 추정치
$t_i$ 는 수준 i에 있는 한 노드의 자식노드의 총 개수
식의 처음 1은 root

최원석

💫

이전 포스트

[알고리즘] Dijkstra’s Algorithm

다음 포스트